数据结构从入门到精通——栈

news2024/10/5 16:19:15

栈

  • 前言
  • 一、栈
    • 1.1栈的概念及结构
    • 1.2栈的实现
    • 1.3栈的面试题
  • 二、栈的具体实现代码
    • 栈的初始化
    • 栈的销毁
    • 入栈
    • 出栈
    • 返回栈顶元素
    • 返回栈中的元素个数
    • 检测是否为空
    • Stack.h
    • Stack.c
    • test.c

前言

栈，作为一种后进先出（LIFO）的数据结构，在计算机科学中扮演着重要的角色。它的特性使得它在处理函数调用、括号匹配、表达式求值等问题时具有得天独厚的优势。然而，如果我们跳出传统思维的束缚，会发现栈的用途远不止于此。

在现代软件开发中，栈的概念被广泛应用在内存管理、并发控制等多个领域。以内存管理为例，每个线程都有自己的栈空间，用于存储局部变量和函数调用信息。这种隔离保证了线程之间的数据安全，避免了数据混乱和意外覆盖。

同样，在并发控制中，栈也发挥着不可替代的作用。通过维护一个任务栈，系统可以合理地调度和分配计算资源，确保任务按照特定的顺序执行，从而避免了并发访问导致的数据不一致问题。

不仅如此，栈的思想还可以被借鉴到生活的方方面面。想象一下，如果我们将日常生活比作一个栈，那么每一天的生活就是一个新的元素被推入栈中。而当我们结束一天的生活，这个元素就会被从栈中弹出，成为我们宝贵的回忆。这种后进先出的特性使得我们能够更好地珍惜当下，因为每一个现在都会成为过去，而每一个过去都是无法替代的。

在这个意义上，栈不仅仅是一种数据结构，更是一种生活态度。它提醒我们珍惜每一个当下，因为每一个现在都会成为我们未来回忆的一部分。同时，它也告诉我们，在面对困难和挑战时，要敢于迎难而上，因为只有这样，我们才能不断成长和进步。

一、栈

1.1栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。

进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

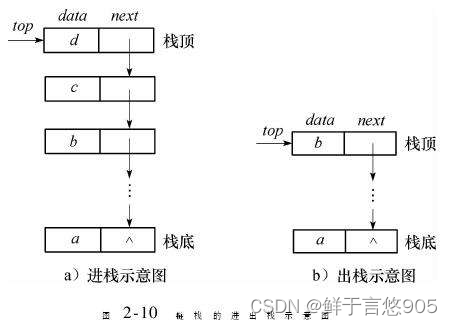
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据也在栈顶。
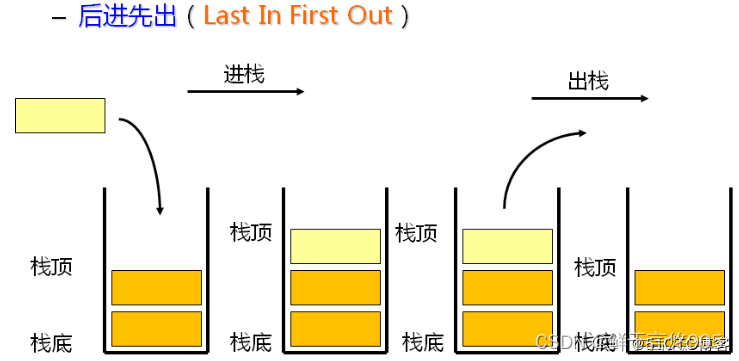
在这里插入图片描述
Push是入栈

Pop是出栈
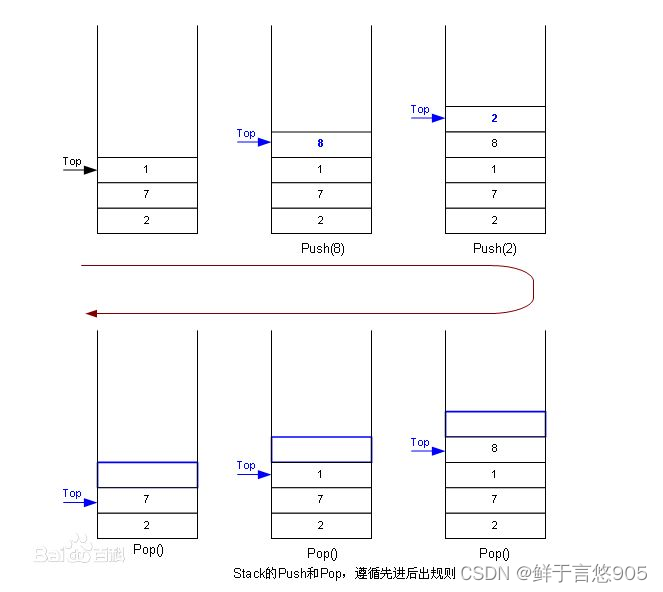
在这里插入图片描述

1.2栈的实现

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。

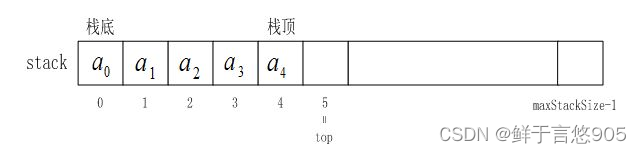
在这里插入图片描述

在这里插入图片描述

// 下面是定长的静态栈的结构，实际中一般不实用，所以我们主要实现下面的支持动态增长的栈
typedef int STDataType;
#define N 10
typedef struct Stack
{
 STDataType _a[N];
 int _top; // 栈顶
}Stack;
 
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
 STDataType* _a;
 int _top; // 栈顶
 int _capacity; // 容量 
}Stack;
// 初始化栈 
void StackInit(Stack* ps); 
// 入栈 
void StackPush(Stack* ps, STDataType data); 
// 出栈 
void StackPop(Stack* ps); 
// 获取栈顶元素 
STDataType StackTop(Stack* ps); 
// 获取栈中有效元素个数 
int StackSize(Stack* ps); 
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps); 
// 销毁栈 
void StackDestroy(Stack* ps);

1.3栈的面试题

  1. 括号匹配问题

  2. 一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出栈的顺序是（ ）。
    A. 12345ABCDE
    B. EDCBA54321
    C. ABCDE12345
    D. 54321EDCBA

  3. 若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（）
    A 1,4,3,2
    B 2,3,4,1
    C 3,1,4,2
    D 3,4,2,1

答案：B C

二、栈的具体实现代码

有关栈，虽然数组类型的栈类型结构更优，但在实际写题目的过程中，链表形式的栈更适用些，接下来我将实现一下链栈

栈的初始化

void STInit(ST* ps);//栈的初始化

void STInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = -1;//或者ps->top = 0;具体区别在于先++还是后++
}

栈的初始化是数据结构中栈操作的第一步，它涉及为栈分配内存空间并设置其初始状态。栈是一种后进先出（LIFO）的数据结构，这意味着最后一个被放入栈中的元素将是第一个被取出的元素。

在进行栈的初始化时，我们需要考虑几个关键步骤。首先，我们需要为栈定义一个合适的数据结构，这通常是一个数组或链表。数组实现的栈在内存中使用连续空间，而链表实现的栈则更为灵活，但可能会占用更多的内存。

接下来，我们需要为栈分配内存空间。对于数组实现的栈，这通常意味着创建一个固定大小的数组来存储栈元素。对于链表实现的栈，我们需要创建一个空的链表节点作为栈顶。

在分配了内存空间之后，我们需要设置栈的初始状态。这通常意味着将栈顶指针或引用设置为一个表示栈为空的状态。对于数组实现的栈，这通常是数组的第一个位置或最后一个位置的索引。对于链表实现的栈，这通常是一个指向空链表节点的指针。

完成栈的初始化后，我们就可以开始执行栈的基本操作，如入栈（push）、出栈（pop）、查看栈顶元素（top）以及判断栈是否为空（is_empty）等。这些操作需要确保遵循栈的后进先出原则。

栈的销毁

void STDestroy(ST* ps);//栈的销毁

void STDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = -1;
}

栈的销毁是栈生命周期中的最后一个阶段，它标志着栈内所有数据元素的释放和栈结构本身的解除。在进行栈的销毁之前，必须确保栈中没有任何数据元素，否则可能会导致数据丢失或内存泄漏。

栈的销毁过程通常包括以下几个步骤：

首先，需要遍历栈内的所有元素，并将它们逐一释放。这通常涉及到调用每个元素的析构函数（如果是C++等支持面向对象编程的语言）或相应的清理函数（如果是C等过程式编程语言），以确保每个元素在被销毁前能够正确地完成其生命周期内的所有任务，如关闭文件、释放内存等。

其次，需要销毁栈本身的数据结构。这通常意味着释放栈所占用的内存空间。在大多数编程语言中，这可以通过调用类似于free（C语言）或delete（C++）这样的内存管理函数来完成。一旦栈的数据结构被销毁，它就不再是一个有效的栈，不能再执行入栈、出栈等操作。

最后，为了确保栈确实已经被销毁，可以在销毁后进行一些检查操作。例如，可以尝试对栈执行一些操作，如入栈或出栈，并检查是否会引发错误或异常。如果程序能够正确地检测到栈已经被销毁，并采取相应的错误处理措施，那么这就可以作为栈销毁过程完成的一个标志。

总的来说，栈的销毁是一个非常重要的过程，它确保了栈在不再需要时能够正确地释放其占用的资源，防止了内存泄漏和其他潜在的资源管理问题。同时，通过销毁栈，也可以为其他需要使用这些资源的操作提供空间，从而提高了整个程序的效率和可靠性。

入栈

//入栈
void STPush(ST* ps,STDatatype x);

void STPush(ST* ps,STDatatype x)
{
	assert(ps);
	ps->top++;
	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDatatype* p = (STDatatype*)realloc(ps->a, sizeof(STDatatype)*newcapacity);
		if (p == NULL)
		{
			perror("p malloc : ");
			return 0;
		}
		ps->a = p;
		ps->capacity = newcapacity;
	}
	ps->a[ps->top] = x;
}

“入栈”（Push）是栈（Stack）这种数据结构中的一个基本操作。栈是一种遵循后进先出（Last In First Out，简称LIFO）原则的数据结构，意味着最后放入栈中的元素将会是第一个被取出的。

“入栈”操作的具体含义是：

  1. 添加元素：将一个元素添加到栈的顶部。
  2. 栈顶变化：由于新元素被添加到栈顶，所以栈顶指针或引用会更新，指向这个新添加的元素。
  3. 栈大小变化：栈的大小（或容量）会增加，因为多了一个元素。

例如，假设我们有一个空的栈，并且按照以下顺序执行入栈操作：

  1. 入栈 A
  2. 入栈 B
  3. 入栈 C

那么，栈的当前状态将是 C 在顶部，B 在中间，A 在底部。如果我们现在执行出栈（Pop）操作，C 将被取出，接着是 B，最后是 A。

在实际应用中，栈常用于保存函数调用过程中的局部变量、参数和返回地址，实现递归调用，以及进行深度优先搜索等。

入栈，是每一个数据处理流程中不可或缺的一环。在信息技术的世界里，数据就如同图书馆的藏书，需要有序地存放和取用。而栈，便是这个数字世界中的一个小巧精致的藏书阁，它遵循着后进先出（LIFO）的规则，每一份数据都像是一本书，被轻轻放在栈顶，等待着被取用或者再次被存放。

每当有新的数据需要处理时，它就会被推入栈中。这个过程就像是图书馆里新到了一本畅销书，图书管理员会将它放在最显眼的位置，供读者最先取阅。同样，栈顶的数据也是最先被处理的，因为它是最后进栈的。这种有序的处理方式，保证了数据处理的效率和准确性。

然而，栈并非万能的。它的规则简单而明确，但也因此有局限性。有时候，我们需要按照不同的顺序来处理数据，这时候就需要使用到队列等其他数据结构。但无论如何，栈都是数据处理中不可或缺的一部分。

在软件开发的世界里，栈的作用更是举足轻重。函数调用、递归算法、异常处理等，都离不开栈的支持。每当一个函数被调用时，它的相关信息就会被压入调用栈中，等待函数执行完毕后弹出。这使得程序能够准确地跟踪函数的执行顺序，保证程序的正确运行。

同时，栈也是内存管理的重要手段。在编程中，我们经常需要动态地分配和释放内存。而栈就是内存分配的一种方式。它会自动管理分配给每个函数的内存空间，当函数执行完毕后，这些内存空间就会被自动释放，避免了内存泄漏等问题的发生。

总的来说，入栈是数据处理和程序运行中的关键步骤。它保证了数据的有序性和程序的正确性，是信息技术世界中不可或缺的一环。在未来的技术发展中，栈的作用将更加重要，我们也需要更加深入地理解和应用它。

出栈

//出栈
void STPop(ST* ps);

void STPop(ST* ps)
{
	assert(ps);
	assert(!STEmpty(&ps));
	ps->top--;
}

当元素从栈的顶部被移除时，这个过程被称为“出栈”。栈是一种遵循后进先出（LIFO）原则的数据结构，其中新元素总是被添加到栈顶，而只有栈顶的元素可以被移除。出栈操作会减少栈的大小，并返回被移除的元素。如果栈为空，则无法进行出栈操作。

返回栈顶元素

STDatatype STTop(ST* ps);//返回栈顶元素

STDatatype STTop(ST* ps)
{
	assert(ps);
	assert(!STEmpty(&ps));
	return ps->a[ps->top];
}

返回栈中的元素个数

int STSize(ST* ps);//返回栈中的元素个数

int STSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

检测是否为空

注意：在使用VS2022编译器编译C语言需要用到布尔类型的时候，需要添加头文件#include <stdbool.h>，添加了这个头文件才能使用布尔类型

bool STEmpty(ST* ps);//检测是否为空

bool STEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

Stack.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef int STDatatype;
typedef struct Stack
{
	STDatatype* a;
	int top;
	int capacity;
}ST;

void STInit(ST* ps);//栈的初始化
void STDestroy(ST* ps);//栈的销毁

//入栈
void STPush(ST* ps,STDatatype x);
//出栈
void STPop(ST* ps);
STDatatype STTop(ST* ps);//返回栈顶元素
int STSize(ST* ps);//返回栈中的元素个数
bool STEmpty(ST* ps);//检测是否为空

Stack.c

#include "Stack.h"

void STInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = -1;//或者ps->top = 0;具体区别在于先++还是后++
}
void STDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = -1;
}
void STPush(ST* ps,STDatatype x)
{
	assert(ps);
	ps->top++;
	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDatatype* p = (STDatatype*)realloc(ps->a, sizeof(STDatatype)*newcapacity);
		if (p == NULL)
		{
			perror("p malloc : ");
			return 0;
		}
		ps->a = p;
		ps->capacity = newcapacity;
	}
	ps->a[ps->top] = x;
}
void STPop(ST* ps)
{
	assert(ps);
	assert(!STEmpty(&ps));
	ps->top--;
}

bool STEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}
STDatatype STTop(ST* ps)
{
	assert(ps);
	assert(!STEmpty(&ps));
	return ps->a[ps->top];
}
int STSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

test.c

#include"Stack.h"

int main()
{
	ST s;
	STInit(&s);
	STPush(&s, 1);
	STPush(&s, 2);
	STPush(&s, 3);

	int top = STTop(&s);
	printf("%d ", top);
	STPop(&s);

	STPush(&s, 4);
	STPush(&s, 5);

	while (!STEmpty(&s))
	{
		int top = STTop(&s);
		printf("%d ", top);
		STPop(&s);
	}

	STDestroy(&s);

	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1500319.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

力扣大厂热门面试算法题 6-8

力扣大厂热门面试算法题 6-8

6. Z 字形变换&#xff0c;7. 整数反转&#xff0c;8. 字符串转换整数 (atoi)&#xff0c;每题做详细思路梳理&#xff0c;配套Python&Java双语代码&#xff0c; 2024.03.08 可通过leetcode所有测试用例。 目录 6. Z 字形变换 解题思路 边界条件 完整代码 Python Ja…
阅读更多...
李想已经5天没发微博了

李想已经5天没发微博了

李想的微博已经5天没更新了。 理想MEGA发布之后的第二天&#xff0c;李想在微博转发了一条某汽车自媒体和理想MEGA设计师BenBaum的访谈视频&#xff0c;并配文表示&#xff0c;Ben的访谈非常好。 不过&#xff0c;在之后的5天时间里&#xff0c;李想的微博便悄无声息了。这与“…
阅读更多...
yocto本地离线构建时报错

yocto本地离线构建时报错

解决方案&#xff1a;在local.conf中添加 BB_NO_NETWORK "1"禁用网络&#xff0c;从本地downloads中fetch源码
阅读更多...
【方法】如何打开7Z分卷压缩文件？

【方法】如何打开7Z分卷压缩文件？

什么是7Z分卷压缩文件&#xff1f;就是在压缩文件时&#xff0c;将文件压缩成若干个大小一样、以“文件名.7z.序号”格式命名的7Z压缩包&#xff0c;可以方便存储和传输&#xff0c;如下图所示。 一、7Z分卷压缩文件如何打开&#xff1f; 我们只需要按照普通压缩包的打开方式&…
阅读更多...
智慧园区综合运营数字化解决方案

智慧园区综合运营数字化解决方案

1. 楼栋管理 2. 物业管理 3. 安防管理 4. 门禁管理 5. 停车管理 6. 能源管理 7. 环保管理 8. 园区生活服务 9. 招商管理 10. 收费中心 11. 园区地图 12. 门户网站 智慧园区软件方案&#xff1a;智慧园区软件解决方案&#xff0c;园区运营管理系统&#xff08;源码&#xff09;-…
阅读更多...
DiT：Scalable Diffusion Models with Transformers

DiT：Scalable Diffusion Models with Transformers

TOC 1 前言2 方法和代码 1 前言 该论文发表之前&#xff0c;市面上几乎都是用卷积网络作为实际意义上的&#xff08;de-facto&#xff09;backbone。于是一个想法就来了&#xff1a;为啥不用transformer作为backbone呢&#xff1f; 文章说本论文的意义就在于揭示模型选择对于…
阅读更多...
二叉树—层序遍历

二叉树—层序遍历

102. 二叉树的层序遍历 代码实现&#xff1a; /*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ /*** Return an array of arrays of size *returnSize.* The sizes of the arrays …
阅读更多...
L波段光端机-L波段+CATV射频光端机工作机制及行业应用探究

L波段光端机-L波段+CATV射频光端机工作机制及行业应用探究

L波段光端机-L波段CATV射频光端机工作机制及行业应用探究 北京海特伟业任洪卓发布于2023年3月8日 一、何为L波段光端机 L波段光端机是一种用于光通信的设备&#xff0c;其主要工作波长位于L波段&#xff0c;即40~860MHz和950~2600MHz的带宽&#xff0c;可选独立工作于950~260…
阅读更多...
开发Chrome扩展插件

开发Chrome扩展插件

1.首先开发谷歌chrome扩展插件&#xff0c;没有严格的项目结构目录&#xff0c;但是需要保证里面有一个mainfest.json文件 (必不可少的文件)。在这个文件里有三个属性必不可少&#xff1a;name、version、mainfest_version&#xff1b; // 清单文件的版本&#xff0c;这个必须写…
阅读更多...
消息队列-Kafka-消费方如何分区与分区重平衡

消息队列-Kafka-消费方如何分区与分区重平衡

消费分区 资料来源于网络 消费者订阅的入口&#xff1a;KafkaConsumer#subscribe 消费者消费的入口&#xff1a;KafkaConsumer#poll 处理流程&#xff1a; 对元数据重平衡处理&#xff1a;KafkaConsumer#updateAssignmentMetadataIfNeeded 协调器的拉取处理&#xff1a;onsum…
阅读更多...
java常用排序算法——冒泡排序，选择排序概述

java常用排序算法——冒泡排序，选择排序概述

前言&#xff1a; 开始接触算法了&#xff0c;记录下心得。打好基础&#xff0c;daydayup! 算法 算法是指解决某个实际问题的过程和方法 排序算法 排序算法指给混乱数组排序的算法。常见的有&#xff1a;冒泡排序&#xff0c;选择排序 冒泡排序&#xff1a; 冒泡排序指在数组…
阅读更多...
python异常机制

python异常机制

当代码出现异常后底下代码都不会被执行了&#xff0c;也就是程序崩溃了。当然能避免异常的话尽量避免但是有的时候这个是没有办法避免的。 异常处理 &#xff08;注&#xff1a;异常处理是从上往下处理&#xff0c;所以编写代码时要注意&#xff09; 语法 try:可能出现异常…
阅读更多...
SpringCloud-SpringBoot读取Nacos上的配置文件

SpringCloud-SpringBoot读取Nacos上的配置文件

在 Spring Boot 应用程序中&#xff0c;可以使用 Spring Cloud Nacos 来实现从 Nacos 服务注册中心和配置中心读取配置信息。以下是如何在 Spring Boot 中读取 Nacos 上的配置文件的步骤&#xff1a; 1. 引入依赖 首先&#xff0c;在 Spring Boot 项目的 pom.xml 文件中添加 …
阅读更多...
JAVA虚拟机实战篇之内存调优[3](诊断问题：MAT工具分析堆内存快照)

JAVA虚拟机实战篇之内存调优[3](诊断问题：MAT工具分析堆内存快照)

文章目录 版权声明解决内存溢出的思路诊断 – 内存快照 MAT内存泄漏检测原理基础知识支配树深堆和浅堆string案例分析 MAT内存泄漏检测原理 导出运行中系统内存快照分析超大堆的内存快照 版权声明 本博客的内容基于我个人学习黑马程序员课程的学习笔记整理而成。我特此声明&am…
阅读更多...
回溯算法题解（难度由小到大）（力扣，洛谷）

回溯算法题解（难度由小到大）（力扣，洛谷）

目录 注意&#xff1a; P1157 组合的输出&#xff08;洛谷&#xff09;https://www.luogu.com.cn/problem/P1157int result[10000] { 0 }; 216. 组合总和 IIIhttps://leetcode.cn/problems/combination-sum-iii/ 17. 电话号码的字母组合https://leetcode.cn/problems/lett…
阅读更多...
YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information

YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information

paper: https://arxiv.org/abs/2402.13616 code YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information 一、引言部分二、问题分析2.1 信息瓶颈原理2.2 可逆函数 三、本文方法3.1 可编程梯度信息 四、实验4.1消融实验部分 今天的深度学习方法关注的…
阅读更多...
ELK介绍使用

ELK介绍使用

文章目录 一、ELK介绍二、Elasticsearch1. ElasticSearch简介&#xff1a;2. Elasticsearch核心概念3. Elasticsearch安装4. Elasticsearch基本操作1. 字段类型介绍2. 索引3. 映射4. 文档 5. Elasticsearch 复杂查询 三、LogStash1. LogStash简介2. LogStash安装 四、kibana1. …
阅读更多...
hv静态资源web服务

hv静态资源web服务

在实际工作中&#xff0c;为了保证App的高可用性&#xff0c;服务端需要缓存一部分静态资源&#xff0c;通过web服务来分发资源。hv即可快速实现web服务。 hv静态资源服务。 HttpService router; router.Static("/statics", "smart-yi-ui");目录结构(sma…
阅读更多...
kafka 可视化工具

kafka 可视化工具

kafka可视化工具 随着科技发展&#xff0c;中间件也百花齐放。平时我们用的redis&#xff0c;我就会通过redisInsight-v2 来查询数据&#xff0c;mysql就会使用goland-ide插件来查询&#xff0c;都挺方便。但是kafka可视化工具就找了半天&#xff0c;最后还是觉得redpandadata…
阅读更多...
javaSE-----继承和多态

javaSE-----继承和多态

目录 一.初识继承&#xff1a; 1.1什么是继承&#xff0c;为什么需要继承&#xff1a; 1.2继承的概念与语法&#xff1a; 二.成员的访问&#xff1a; 2.1super关键字 2.2this和super的区别&#xff1a; 三.再谈初始化: 小结&#xff1a; 四.初识多态&#xff1a; 4.1多…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023