目录
78.子集
90.子集||
491.非递减子序列
78.子集
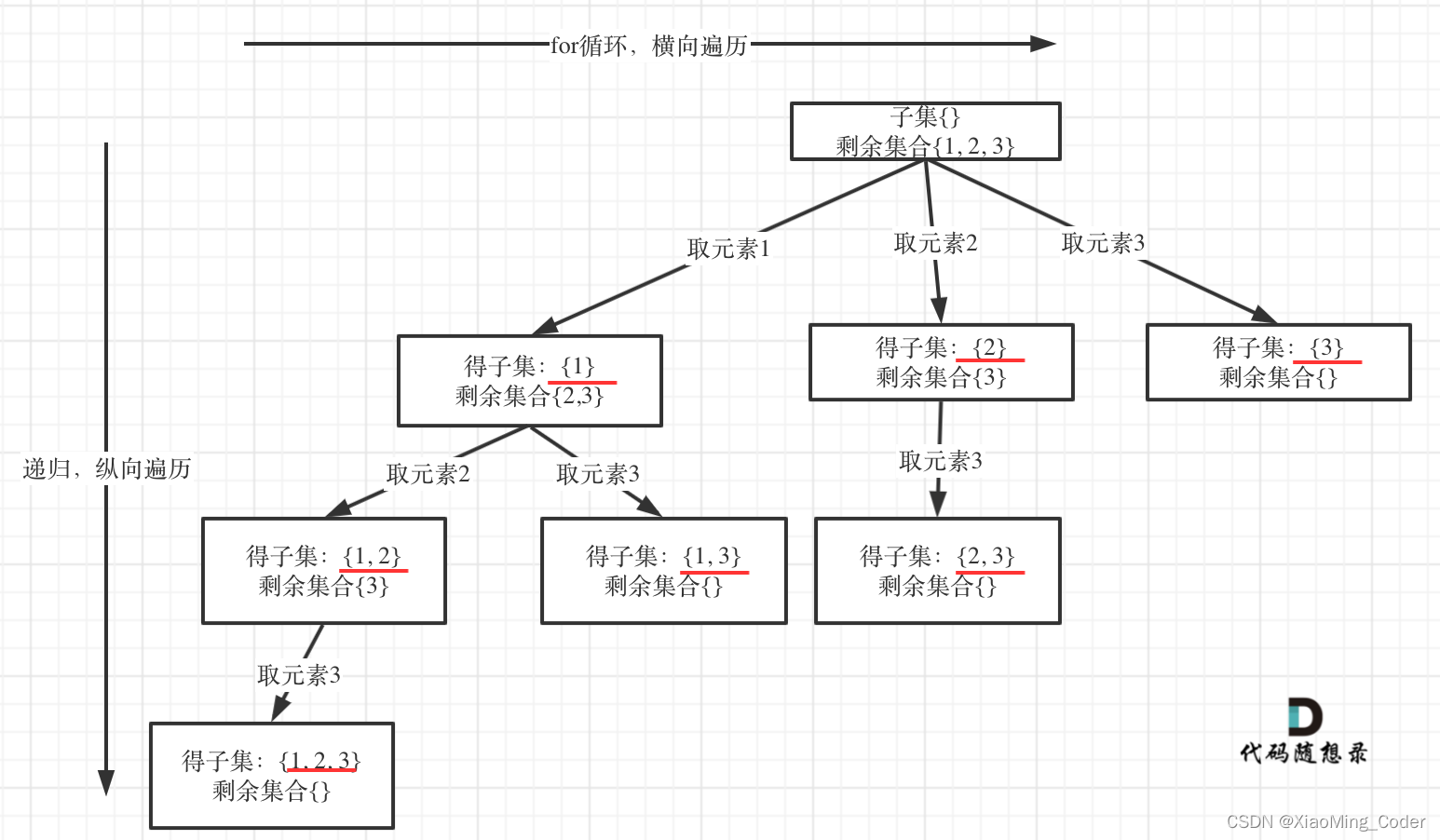
78. 子集
中等
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的
子集
(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0] 输出:[[],[0]]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
class Solution {
// 用于存放所有可能的子集结果
List<List<Integer>> result = new ArrayList<>();
// 用于存放当前正在构建的子集路径
List<Integer> path = new ArrayList<>();
// 主函数,用于获取输入数组的所有子集
public List<List<Integer>> subsets(int[] nums) {
// 从数组的第一个元素开始进行回溯
backtracking(nums, 0);
// 返回所有子集的结果
return result;
}
// 回溯函数,用于构建所有可能的子集
public void backtracking(int[] nums, int begin) {
// 将当前路径添加到结果集中,这里注意要创建一个新的ArrayList来避免后续修改影响到结果集
result.add(new ArrayList<>(path));
// 如果已经遍历到数组的末尾,则结束当前回溯路径
if (begin == nums.length) {
return;
}
// 从当前位置开始遍历数组,选择元素加入子集
for (int i = begin; i < nums.length; i++) {
// 将当前元素加入子集路径
path.add(nums[i]);
// 递归调用,继续构建下一个位置的子集
backtracking(nums, i + 1);
// 回溯,移除刚刚加入的子集路径中的元素,尝试其他可能性
path.removeLast();
}
}
}90.子集||
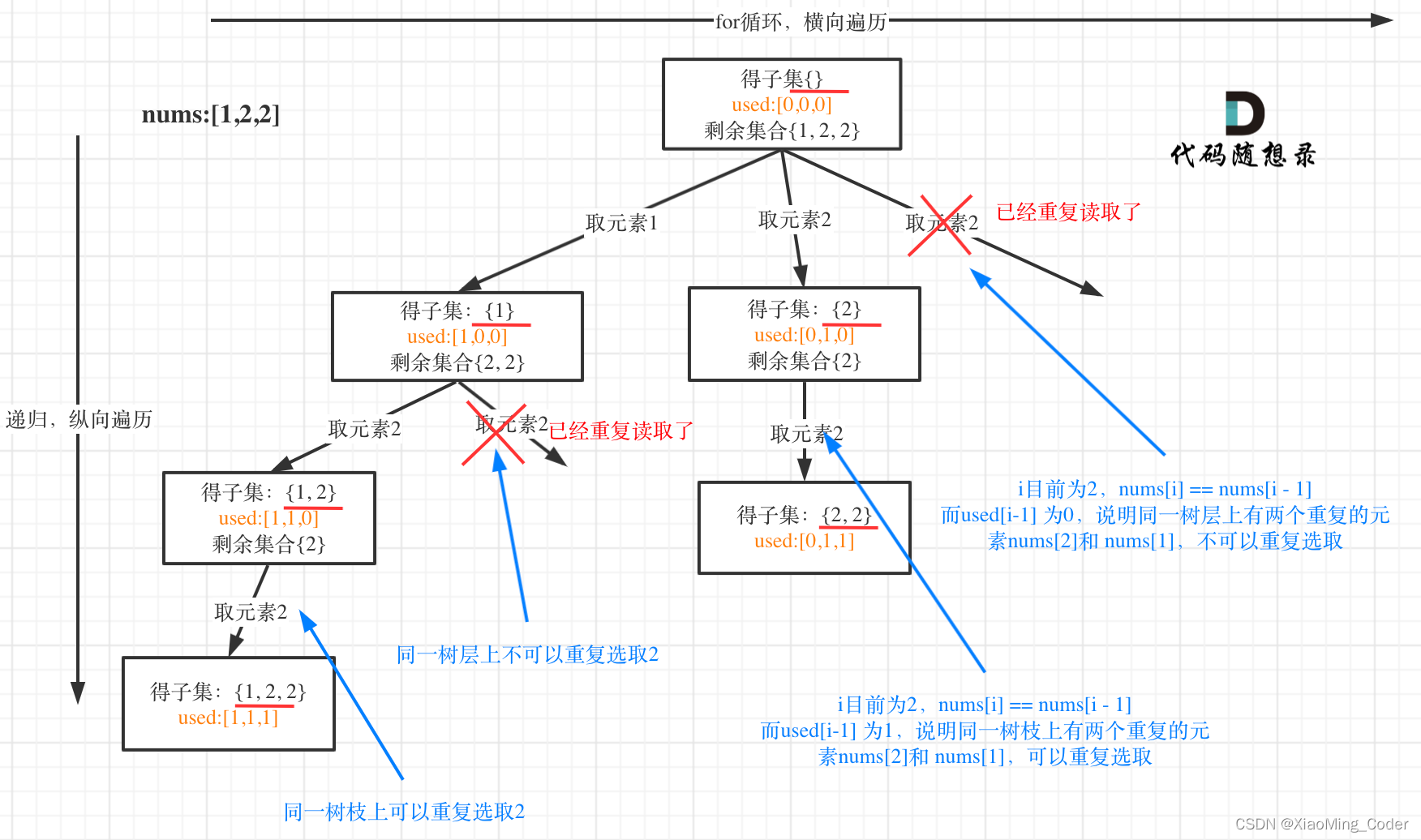
90. 子集 II
中等
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的<span data-keyword="subset">子集</span>(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0] 输出:[[],[0]]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10
注意这里也是树层去重
class Solution {
// 用于存放所有可能的子集结果
List<List<Integer>> result = new ArrayList<>();
// 用于存放当前正在构建的子集路径
List<Integer> path = new ArrayList<>();
// 主函数,用于获取输入数组的所有子集(包括重复元素)
public List<List<Integer>> subsetsWithDup(int[] nums) {
// 先对数组进行排序,这样相同的元素会相邻,便于去重
Arrays.sort(nums);
// 从数组的第一个元素开始进行回溯
backtracking(nums, 0);
// 返回所有子集的结果
return result;
}
// 回溯函数,用于构建所有可能的子集
public void backtracking(int[] nums, int begin) {
// 将当前路径添加到结果集中,注意要创建一个新的ArrayList来避免后续修改影响到结果集
result.add(new ArrayList<>(path));
// 如果已经遍历到数组的末尾,则结束当前回溯路径
if (begin == nums.length) {
return;
}
// 从当前位置开始遍历数组,选择元素加入子集
for (int i = begin; i < nums.length; i++) {
// 如果当前元素和前一个元素相同,并且不是从begin开始的第一个元素(即不是第一个出现的重复元素),则跳过,避免重复子集
if (i > begin && nums[i] == nums[i - 1]) {
continue;
}
// 将当前元素加入子集路径
path.add(nums[i]);
// 递归调用,继续构建下一个位置的子集
backtracking(nums, i + 1);
// 回溯,移除刚刚加入的子集路径中的元素,尝试其他可能性
path.removeLast();
}
}
}491.非递减子序列
491. 非递减子序列
中等
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例 1:
输入:nums = [4,6,7,7] 输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
示例 2:
输入:nums = [4,4,3,2,1] 输出:[[4,4]]
提示:
1 <= nums.length <= 15-100 <= nums[i] <= 100
看到这道题我的第一反应是
class Solution {
// 存储所有满足条件的递增子序列的结果集合
List<List<Integer>> result = new ArrayList<>();
// 用于构建当前递增子序列的临时路径
List<Integer> path = new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
// 调用回溯函数,从数组的第一个元素开始寻找递增子序列
backtracking(nums, 0);
// 返回所有满足条件的递增子序列
return result;
}
public void backtracking(int[] nums, int begin) {
// 如果当前路径中的元素个数大于等于2,则将路径添加到结果集合中
if (path.size() >= 2) {
result.add(new ArrayList<>(path));
}
// 如果已经遍历到数组的末尾,则回溯结束
if (begin == nums.length) {
return;
}
// 从begin位置开始遍历数组
for (int i = begin; i < nums.length; i++) {
// 如果当前元素与前一个元素相同且不是序列的第一个元素,则跳过以避免重复
if (i > begin && nums[i] == nums[i - 1]) {
continue;
}
// 如果当前路径为空,或者当前元素大于等于路径中的最后一个元素,则继续构建子序列
if (path.isEmpty() || nums[i] >= path.get(path.size() - 1)) {
// 将当前元素添加到路径中
path.add(nums[i]);
// 递归调用,继续构建子序列,从下一个元素开始
backtracking(nums, i + 1);
// 回溯,将当前元素从路径中移除,探索其他可能性
path.removeLast();
}
}
}
}后来发现这道题的原数组是不能排序的,会破坏结果,用数组或者map来去重,这里使用数组
同样是树层去重
class Solution {
// 结果集合,存储所有满足条件的递增子序列
List<List<Integer>> res = new ArrayList<>();
// 路径集合,用于构建当前递增子序列
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
// 从数组的第一个元素开始,寻找所有递增子序列
backtracking(nums, 0);
// 返回所有满足条件的子序列
return res;
}
private void backtracking(int[] nums, int begin) {
// 如果当前路径中的元素数量大于1,则将其作为一个有效的递增子序列加入结果集
if (path.size() > 1) {
res.add(new ArrayList<>(path));
// 注意这里不要加return,要取树上的节点
// 不能在这里return,因为需要继续探索当前路径下可能的其他子序列
}
// 创建一个used数组来记录当前遍历过程中每个数字是否被使用过
// 用于避免将重复数字添加到子序列中
int[] used = new int[201];
// 从begin位置开始遍历数组
for (int i = begin; i < nums.length; i++) {
// 如果当前数字在本层遍历中已经被使用过,跳过防止重复
if (used[nums[i] + 100] == 1) {
continue;
}
// 如果当前路径为空,或者当前元素大于等于路径中的最后一个元素,则继续构建子序列
if (path.isEmpty() || nums[i] >= path.get(path.size() - 1)) {
//标记该数字被使用过
used[nums[i] + 100] = 1;
// 将当前元素添加到路径中
path.add(nums[i]);
// 递归调用,继续构建子序列,从下一个元素开始
backtracking(nums, i + 1);
// 回溯,将当前元素从路径中移除,探索其他可能性
path.removeLast();
}
}
}
}