Python算法题集_N 皇后
- 题51:N 皇后
- 1. 示例说明
- 2. 题目解析
- - 题意分解
- - 优化思路
- - 测量工具
- 3. 代码展开
- 1) 标准求解【规则遍历合理性+回溯】
- 2) 改进版一【线状态检测合理性+回溯】
- 3) 改进版二【单行矩阵+回溯】
- 4. 最优算法
- 5. 相关资源
本文为Python算法题集之一的代码示例
题51:N 皇后
1. 示例说明
-
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将
n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数
n,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中
'Q'和'.'分别代表了皇后和空位。示例 1:
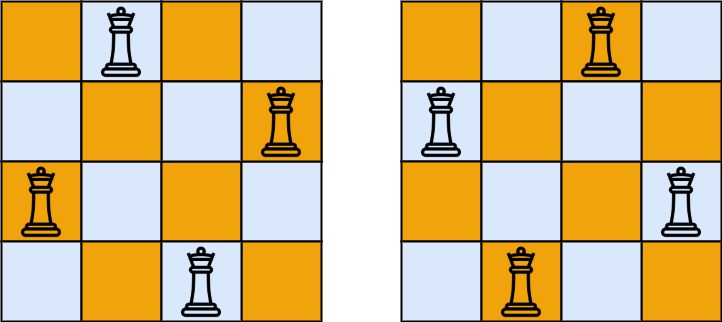
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。示例 2:
输入:n = 1 输出:[["Q"]]提示:
1 <= n <= 9
2. 题目解析
- 题意分解
- 本题是在矩阵内摆放Q皇后,并且不违反规则的问题
- 矩阵大小为nn,要放n个Q皇后,代表每行、每列最多有一个Q皇后;额外的规则是斜线,左斜线有(2n-1)条,右斜线有(2*n-1)条【类似2.5d地图】
- 核心计算有两层,一是回溯遍历,二是当前位置Q是否合乎规则判断
- 回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法。
- 优化思路
-
通常优化:减少循环层次
-
通常优化:增加分支,减少计算集
-
通常优化:采用内置算法来提升计算速度
-
分析题目特点,分析最优解
-
可以进行规则遍历进行合理性函数检测
-
可以保存列、左斜线、右斜线是否被占据的状态,通过线状态检测判定是否合理
-
因每行仅有一个Q皇后,因此整个矩阵可以用一维列表保存,位置代表行,值代表此行的Q皇后列下标
-
- 测量工具
- 本地化测试说明:LeetCode网站测试运行时数据波动很大【可把页面视为功能测试】,因此需要本地化测试解决数据波动问题
CheckFuncPerf(本地化函数用时和内存占用测试模块)已上传到CSDN,地址:Python算法题集_检测函数用时和内存占用的模块- 本题本地化超时测试用例自己生成,详见章节【最优算法】,代码文件包含在【相关资源】中
3. 代码展开
1) 标准求解【规则遍历合理性+回溯】
通过规则遍历的合理性函数,实现回溯求解
页面功能测试,凄凄惨惨,超过28%
import CheckFuncPerf as cfp
class Solution:
def solveNQueens_base(self, n):
def isValid(board, row, col):
ilen = len(board)
for irow in range(row):
if board[irow][col] == 'Q':
return False
for irow, icol in zip(range(row - 1, -1, -1), range(col + 1, ilen, 1)):
if board[irow][icol] == 'Q':
return False
for irow, icol in zip(range(row - 1, -1, -1), range(col - 1, -1, -1)):
if board[irow][icol] == 'Q':
return False
return True
board = [['.'] * n for x in range(n)]
result, isize = [], n
def backtrack(irow):
if irow == isize:
tmpmap = [''.join(x) for x in board]
result.append(tmpmap)
return
for icol in range(isize):
if not isValid(board, irow, icol):
continue
board[irow][icol] = 'Q'
backtrack(irow + 1)
board[irow][icol] = '.'
backtrack(0)
return result
aSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.solveNQueens_base, ilen)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
# 运行结果
函数 solveNQueens_base 的运行时间为 61887.03 ms;内存使用量为 75908.00 KB 执行结果 = 73712
2) 改进版一【线状态检测合理性+回溯】
通过线状态检测位置合理性,实现回溯求解,此检测方法实际上将二维平面的遍历转化为了一维的循环,减少了一层循环
页面功能测试,性能一般,超过76%
import CheckFuncPerf as cfp
class Solution:
def solveNQueens_ext1(self, n):
from copy import deepcopy
def backtrack(irow, cols, dgs, adgs, currmap, result):
ilen = len(cols)
if irow == ilen:
result.append(deepcopy(currmap))
return result
for icol in range(ilen):
if cols[icol] or dgs[irow + icol] or adgs[irow - icol + ilen - 1]:
continue
currmap[irow][icol] = "Q"
cols[icol] = True
dgs[irow + icol] = True
adgs[irow - icol + ilen - 1] = True
backtrack(irow + 1, cols, dgs, adgs, currmap, result)
adgs[irow - icol + ilen - 1] = False
dgs[irow + icol] = False
cols[icol] = False
currmap[irow][icol] = "."
statecols = [False for x in range(n)]
statedgs = [False for x in range(2 * n - 1)]
stateadgs = [False for x in range(2 * n - 1)]
currmap = [["." for x in range(n)] for y in range(n)]
result = []
backtrack(0, statecols, statedgs, stateadgs, currmap, result)
for statemap in result:
for irow in range(len(statemap)):
statemap[irow] = "".join(statemap[irow])
return result
aSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.solveNQueens_ext1, ilen)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
# 运行结果
函数 solveNQueens_ext1 的运行时间为 13925.13 ms;内存使用量为 199784.00 KB 执行结果 = 73712
3) 改进版二【单行矩阵+回溯】
使用单行列表存储矩阵,通过计算判断合理性,实现回溯算法
页面功能测试,马马虎虎,超过53%
import CheckFuncPerf as cfp
class Solution:
def solveNQueens_ext2(self, n):
result = []
def nqbacktrack(currmap):
if len(currmap) == n:
result.append(["." * (x-1) +"Q" +"." * (n-x) for x in currmap])
rows = [x for x in range(1, n+1)]
for irow in rows:
if irow in currmap:
continue
tmpFlag = False
for icol, val in enumerate(currmap):
if abs(val-irow) == len(currmap)-icol:
tmpFlag = True
if tmpFlag:
continue
currmap.append(irow)
nqbacktrack(currmap)
currmap.pop()
nqbacktrack([])
return result
aSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.solveNQueens_ext2, ilen)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
# 运行结果
函数 solveNQueens_ext2 的运行时间为 31577.39 ms;内存使用量为 66228.00 KB 执行结果 = 73712
4. 最优算法
根据本地日志分析,最优算法为第2种方式【线状态检测合理性+回溯】solveNQueens_ext1
本题测试数据,似乎能推出以下结论:
- 布尔计算性能优于数值计算
- 减少循环层次可以明显提升性能
ilen = 13
aSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.solveNQueens_base, ilen)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
result = cfp.getTimeMemoryStr(aSolution.solveNQueens_ext1, ilen)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
result = cfp.getTimeMemoryStr(aSolution.solveNQueens_ext2, ilen)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
# 算法本地速度实测比较
函数 solveNQueens_base 的运行时间为 61887.03 ms;内存使用量为 75908.00 KB 执行结果 = 73712
函数 solveNQueens_ext1 的运行时间为 13925.13 ms;内存使用量为 199784.00 KB 执行结果 = 73712
函数 solveNQueens_ext2 的运行时间为 31577.39 ms;内存使用量为 66228.00 KB 执行结果 = 73712
5. 相关资源
本文代码已上传到CSDN,地址:Python算法题源代码_LeetCode(力扣)_N皇后
一日练,一日功,一日不练十日空
may the odds be ever in your favor ~