文章目录
- 编译过程
- 进制转换
- 1、进制的概念
- 1.1 二进制
- 1.2 八进制
- 1.3 十六进制
- 进制在程序中的表现方式
- 十进制转二进制
- 将十进制转换成二进制(除2反序取余法)
- 二进制转十进制(权值法)
- 八进制转十进制
- 将十进制转换成八进制(除8反序取余法)
- 八进制转十进制(权值法)
- 十六进制转十进制
- 将十进制转换成十六进制(除16反序取余法)
- 十六进制转十进制(权值法)
- 快速转换8421法则
- 二进制快速转换八进制
- 二进制快速转换十六进制
- 16进制快速转换2进制
- 浮点型数据转换成2进制
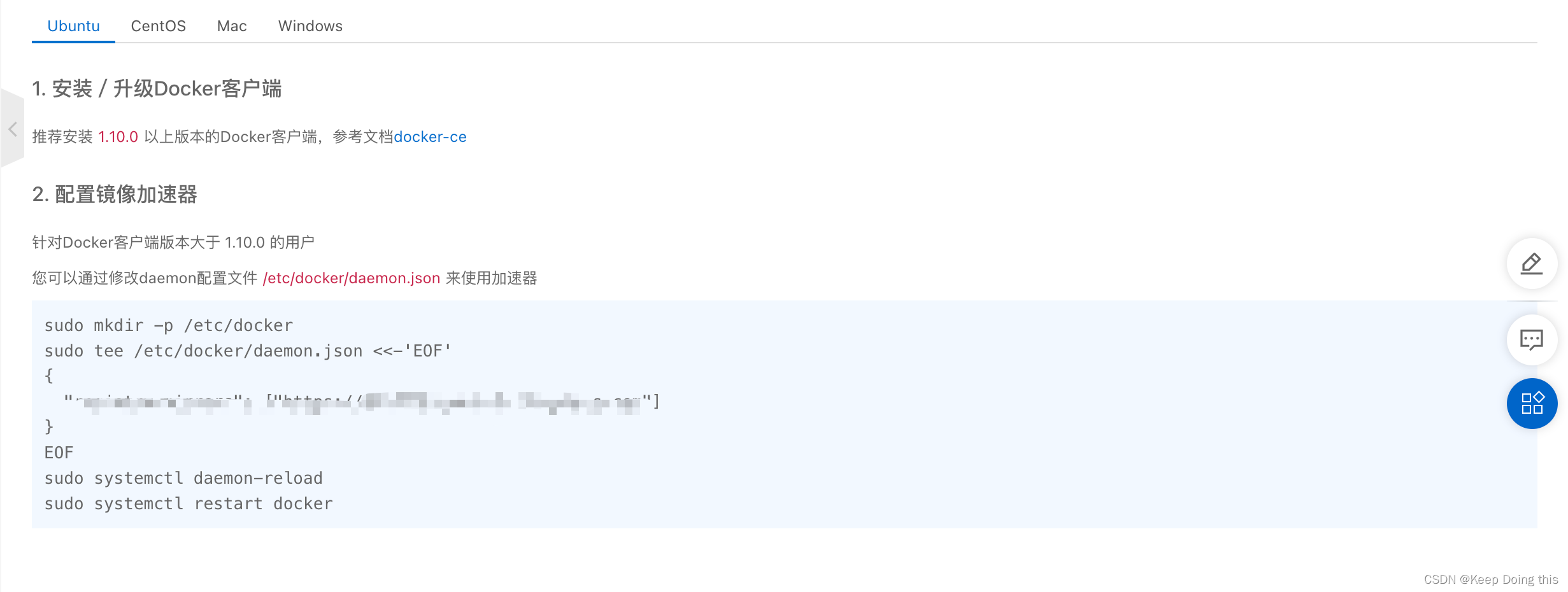
编译过程
1 gcc 源码文件.c -o 可执行文件.exe -o生产exe
helloWorld.c -o hell.exe
1、预处理 宏定义展开、头文件展开、删除注释
gcc -E 源码文件 -o 生成文件.i //gcc -E helloworld.c -o hello.i .i编译文件
2、编译 检查语法,将文件转成汇编文件
gcc -S 预处理生成的.i文件 -o 生成文件.s //gcc -S hello.i -o hello.s .s汇编文件
3、汇编 将汇编文件转成二进制文件
gcc -c hello.s -o hello.o //
4、链接 将C语言链接库链接到程序中
gcc hello.o -o hello.exe
进制转换
1、进制的概念
进制也就是进位制,是人们规定的一种进位方法。 对于任何一种进制—X进制,就表示某一位置上的数运算时是逢X进一位。 十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,x进制就是逢x进位。
1.1 二进制
二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”。
1.2 八进制
八进制,Octal,缩写OCT或O,一种以8为基数的计数法,采用0,1,2,3,4,5,6,7八个数字,逢八进1。一些编程语言中常常以数字0开始表明该数字是八进制。
1.3 十六进制
十六进制(英文名称:Hexadecimal),同我们日常生活中的表示法不一样,它由0-9,A-F组成,字母不区分大小写。与10进制的对应关系是:0-9对应0-9,A-F对应10-15。
进制在程序中的表现方式
| 十进制 | 以正常数字1-9开头,如123 |
|---|---|
| 八进制 | 以数字0开头,如0123 |
| 十六进制 | 以0x开头,如0x123 |
| 二进制 | C语言不能直接书写二进制数 |
| 二进制 | 八进制 | 十六进制 | 十进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | A | 10 |
| 1011 | 13 | B | 11 |
| 1100 | 14 | C | 12 |
| 1101 | 15 | D | 13 |
| 1110 | 16 | E | 14 |
| 1111 | 17 | F | 15 |
| 10000 | 18 | 10 | 16 |
十进制转二进制
将十进制转换成二进制(除2反序取余法)

二进制转十进制(权值法)
从二进制的末尾依次乘以2的n次幂(n是从0 开始的)
小提示: 任何数的0次幂都等于1
任何数的1次幂都等于本身
十进制的 123 使用上面的方法(除2 反序取余法)得到的二进制为1111011
将1111011 转成10进制
1 ∗ 2 0 + 1 ∗ 2 1 + 0 ∗ 2 2 + 1 ∗ 2 3 + 1 ∗ 2 4 + 1 ∗ 2 5 + 1 ∗ 2 6 = 123 1*2^0 + 1*2^1 +0*2^2+1*2^3+1*2^4+1*2^5+1*2^6=123 1∗20+1∗21+0∗22+1∗23+1∗24+1∗25+1∗26=123
八进制转十进制
将十进制转换成八进制(除8反序取余法)

八进制转十进制(权值法)
从八进制的末尾依次乘以8的n次幂(n是从0 开始的)
3
∗
8
0
+
7
∗
8
1
+
1
∗
8
2
=
123
3*8^0+7*8^1+1*8^2 = 123
3∗80+7∗81+1∗82=123
十六进制转十进制
将十进制转换成十六进制(除16反序取余法)

十六进制转十进制(权值法)
从十六进制的末尾依次乘以16的n次幂(n是从0 开始的)
11
∗
1
6
0
+
7
∗
1
6
1
=
123
11*16^0+7*16^1=123
11∗160+7∗161=123
快速转换8421法则
在对应的位置填1
| 4096 | 2048 | 1024 | 512 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 二进制结果 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 十进制的123 | 1111011 | |||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 164 | 10100100 | ||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 2008 | 11111011000 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 2024 | 11111101000 |
二进制快速转换八进制
八进制的数和二进制数可以按位对应(八进制一位对应二进制三位)。
例:
将二进制从末尾3位一隔
十进制: 123
二进制: 1111011
八进制: 011 按照8431 法则 011 = 3
111 按照8431 法则 111 = 7
1 按照8431 法则 011 = 1
转换结果为173
同理: 八进制转换二进制时也是将八进制每一位的值转换成3位2进制就可以了
173
1-------1
7-------111
3-------011
二进制结果就是: 1111011
二进制快速转换十六进制
十六进制的数和二进制数可以按位对应(十六进制一位对应二进制四位)。
例:
将二进制从末尾3位一隔
十进制: 123
二进制: 1111011
十六进制: 1011 按照8431 法则 011 = b
0111 按照8431 法则 111 = 7
转换结果为7b
16进制快速转换2进制
7B
7----------111
B----------1011
结果: 1111011
浮点型数据转换成2进制
十进制的小数转换成二进制:小数部分和2相乘,取整数,不足1取0,每次相乘都是小数部分,顺序看取整后的数就是转化后的结果。(小数位有多少位就乘以多少次) ;从上往下取值;
将小数部分依次乘以2 如果结果中整数部分值为1 取值为1 如果为0 值
为0 小数位数有多少位 乘多少次
double a = 123.4567;
0.4567
*2
0.9134 0
*2
1.8268 1
0.8268
*2
1.6536 1
0.6536
*2
1.3072 1
0.4567 = 0111