● 121. 买卖股票的最佳时机

因为只能买卖一次，所以左边找一个最小的，右边找一个最大的，相减的差就是最大的利润。那么用贪心来做：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        //vector<int> dp(n,vector<int>(n,0));
        int minprice=INT_MAX;
        int result=INT_MIN;
        for(int i=0;i<n;++i){
            minprice=min(minprice,prices[i]);
            result=max(result,prices[i]-minprice);
        }
        return result;
    }
};

回归到动规，动规五部曲：
1.dp数组元素含义。dp[j][0]：第j天持有股票的最大现金(买了还没卖出，是负数)。dp[j][1]：第j天未持有股票的最大现金(非负数，没买或已卖出)。最后返回的是dp[n-1][1]，因为最后手上没股票。

2.递推公式。dp[j][0]=max(dp[j-1][0],-prices[j])。dp[j][1]=max(dp[j-1][1],dp[j][0]+prices[j])。

3.初始化。刚开始现金是0，下标为0的时候对应第一天，第一天只能持有股票，所以dp[0][0]=-prices[i],dp[0][1]=0(不会覆盖后面dp[j][1]取max).

4.遍历顺序。从左到右

5.打印。

代码：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        vector<vector<int>> dp(n,vector<int>(2));
        dp[0][0]=-prices[0];
        dp[0][1]=0;
        for(int j=1;j<n;++j){
            dp[j][0]=max(dp[j-1][0],-prices[j]);
            dp[j][1]=max(dp[j-1][1],dp[j][0]+prices[j]);
        }
        return dp[n-1][1];
    }
};

又∵在循环体中始终只涉及j和j-1的dp数组，所以可以只设置dp数组个数为2的滚动数组，节省空间。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        vector<vector<int>> dp(2,vector<int>(2));
        dp[0][0]=-prices[0];
        dp[0][1]=0;
        for(int j=1;j<n;++j){
            dp[j%2][0]=max(dp[(j-1)%2][0],-prices[j]);
            dp[j%2][1]=max(dp[(j-1)%2][1],dp[j%2][0]+prices[j]);
        }
        return dp[(n-1)%2][1];
    }
};

正如之前说，贪心类的简单的很简单，这道题用贪心很快且好想，用动规五部曲还繁琐一些。但是为下道题目打了基础。

● 122.买卖股票的最佳时机II

这道题是贪心部分做过的一道题，还记得其贪心思路：“第i天买入，第j天卖出”，和“第i天买入，中间每天都既卖出又买入，第j天卖出”一样的效果。可以顺便复习一下之前用贪心的写法。

动规：

1.dp数组含义。

和上面一样：dp[j][0]：第j天持有股票的最大现金。dp[j][1]：第j天未持有股票的最大现金。

2.递推公式。注意和贪心算法的不同，当下标到j，意味着前j-1天的已经处理，不能再动了。

先看dp[j][0]，两种情况：如果前一天j-1持有股票，第j天不能卖仍然得持有，就还等于dp[j-1][0]；如果前一天j-1没有股票，第j天买入，就为dp[j-1][1]-prices[j]。所以dp[j][0]=max( dp[j-1][0], dp[j-1][1]-prices[j])。

再看dp[j][1]，也是两种情况：第j-1天有股票，第j天要卖掉，为dp[j-1][0]+prices[j]；没有股票，第j天不买入，为dp[j-1][1]。所以dp[j][1]=max( dp[j-1][0]+prices[j], dp[j-1][1])。

3.初始化。同上。

4.遍历顺序。同上。

5.打印。

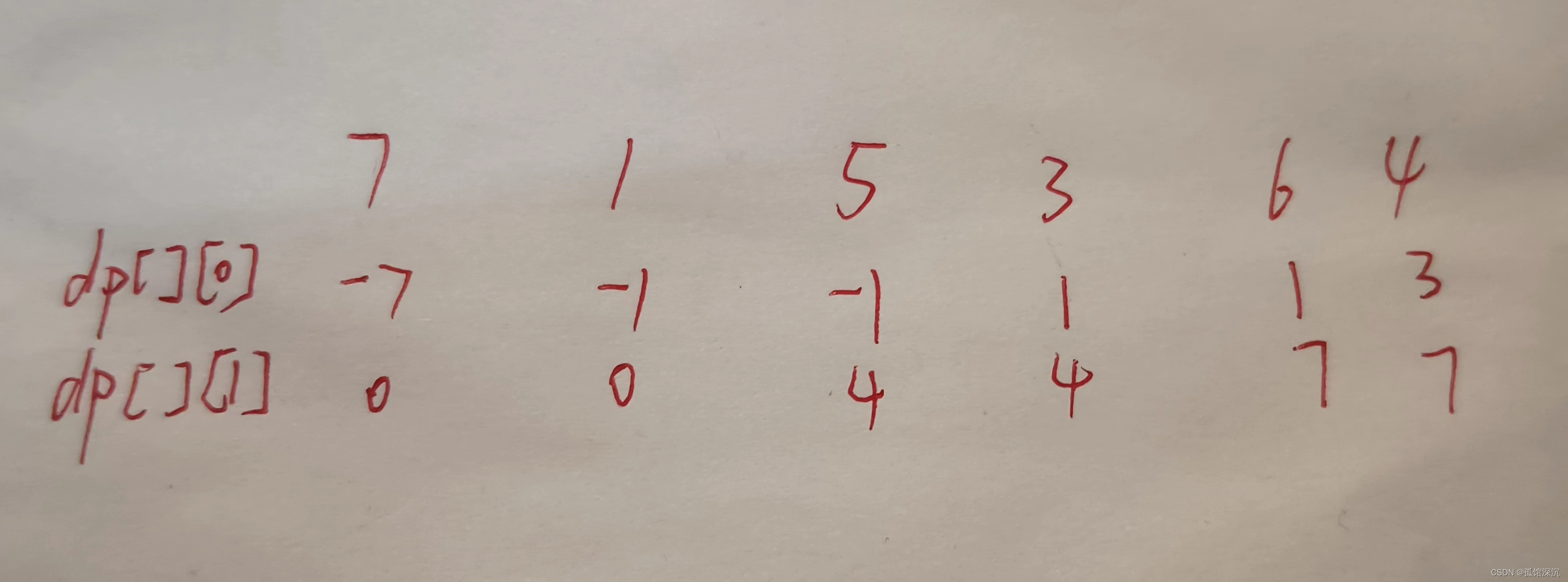
代码如下。可见和上题唯一不同的是递推公式。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        vector<vector<int>> dp(2,vector<int>(2));
        dp[0][0]=-prices[0];
        dp[0][1]=0;
        for(int j=1;j<n;j++){
            dp[j%2][0]=max( dp[(j-1)%2][0], dp[(j-1)%2][1]-prices[j]);
            dp[j%2][1]=max( dp[(j-1)%2][0]+prices[j], dp[(j-1)%2][1]);
        }            
        return dp[(n-1)%2][1];     
    }
};