[ICPC2018 Qingdao R] Plants vs. Zombies
传送门
题面翻译
给定 n n n 个植物和 m m m 的步数限制,每个植物在位置 1 … n 1\dots n 1…n 上。你初始时在位置 0 0 0,每次可以移动到相邻的位置上。
每次设你走完一步后到达的位置是 i i i,则会使得这个位置的植物的高度增加 a i a_i ai。设 d i d_i di 为走完 m m m 步后位置 i i i 的植物高度,求出一个最优的走法使得 min 1 ≤ i ≤ n d i \min\limits_{1 \le i \le n} d_i 1≤i≤nmindi 最大。
2 ≤ n ≤ 1 0 5 2\leq n\leq 10 ^ 5 2≤n≤105, 0 ≤ m ≤ 1 0 12 0\leq m\leq 10 ^ {12} 0≤m≤1012, 1 ≤ a i ≤ 1 0 5 1\leq a_i\leq 10 ^ 5 1≤ai≤105, ∑ n ≤ 1 0 6 \sum n\leq 10 ^ 6 ∑n≤106。
题目描述
BaoBao and DreamGrid are playing the game Plants vs. Zombies \textit{Plants vs. Zombies} Plants vs. Zombies. In the game, DreamGrid grows plants to defend his garden against BaoBao’s zombies.

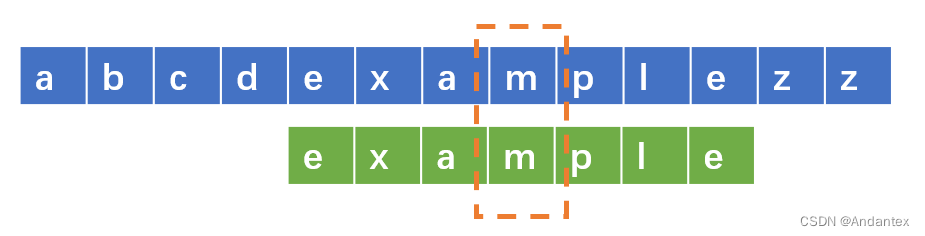
Plants vs. Zombies(?) (Image from pixiv. ID: 21790160; Artist: socha) \textit{Plants vs. Zombies(?)} \\ \textit{(Image from pixiv. ID: 21790160; Artist: socha)} Plants vs. Zombies(?)(Image from pixiv. ID: 21790160; Artist: socha)
There are n n n plants in DreamGrid’s garden arranged in a line. From west to east, the plants are numbered from 1 to n n n and the i i i-th plant lies i i i meters to the east of DreamGrid’s house. The i i i-th plant has a defense value of d i d_i di and a growth speed of a i a_i ai. Initially, d i = 0 d_i = 0 di=0 for all 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n.
DreamGrid uses a robot to water the plants. The robot is in his house initially. In one step of watering, DreamGrid will choose a direction (east or west) and the robot moves exactly 1 meter along the direction. After moving, if the i i i-th plant is at the robot’s position, the robot will water the plant and a i a_i ai will be added to d i d_i di. Because the water in the robot is limited, at most m m m steps can be done.
The defense value of the garden is defined as min { d i ∣ 1 ≤ i ≤ n } \min\{d_i | 1 \le i \le n\} min{di∣1≤i≤n}. DreamGrid needs your help to maximize the garden’s defense value and win the game.
- Each time the robot MUST move before watering a plant;
- It’s OK for the robot to move more than n n n meters to the east away from the house, or move back into the house, or even move to the west of the house.
输入格式
There are multiple test cases. The first line of the input contains an integer T T T, indicating the number of test cases. For each test case:
The first line contains two integers n n n and m m m ( 2 ≤ n ≤ 1 0 5 2 \le n \le 10^5 2≤n≤105, 0 ≤ m ≤ 1 0 12 0 \le m \le 10^{12} 0≤m≤1012), indicating the number of plants and the maximum number of steps the robot can take.
The second line contains n n n integers a 1 , a 2 , . . . , a n a_1, a_2, ... , a_n a1,a2,...,an ( 1 ≤ a i ≤ 1 0 5 1 \le a_i \le 10^5 1≤ai≤105), where a i a_i ai indicates the growth speed of the i i i-th plant.
It’s guaranteed that the sum of n n n in all test cases will not exceed 1 0 6 10^6 106.
输出格式
For each test case output one line containing one integer, indicating the maximum defense value of the garden DreamGrid can get.
样例 #1
样例输入 #1
2
4 8
3 2 6 6
3 9
10 10 1
样例输出 #1
6
4
提示
In the explanation below, E indicates that the robot moves exactly 1 meter to the east from his current position, and W indicates that the robot moves exactly 1 meter to the west from his current position.
For the first test case, a candidate direction sequence is { E , E , W , E , E , W , E , E } \{E, E, W, E, E, W, E, E\} {E,E,W,E,E,W,E,E}, so that we have d = { 6 , 6 , 12 , 6 } d = \{6,6,12,6\} d={6,6,12,6} after the watering.
For the second test case, a candidate direction sequence is { E , E , E , E , W , E , W , E , W } \{E, E, E, E, W, E, W, E, W\} {E,E,E,E,W,E,W,E,W}, so that we have d = { 10 , 10 , 4 } d = \{10, 10, 4\} d={10,10,4} after the watering.
注明
以上来自洛谷。 以上来自洛谷。 以上来自洛谷。
解题思路
题目中让我们求最小值最大,并具有单调性,所以可以二分答案。对于二分答案,这里不细讲。
以下为验证函数的写法:
- 先让一个数组 T o n g Tong Tong 满足 T o n g i × d i ≥ m i d d l e Tong_i ×d_i \ge middle Tongi×di≥middle;
- 对于 T o n g i ≥ 1 Tong_i \ge 1 Tongi≥1 都需要在 T o n g i Tong_i Tongi 与 T o n g i + 1 Tong_{i+1} Tongi+1 之间走 2 × T o n g i − 1 2\times Tong_i −1 2×Tongi−1 次才能满足条件,而 T o n g i + 1 Tong_{i+1} Tongi+1 项也要去掉 T o n g i − 1 Tong_i −1 Tongi−1 次;
- 若走的总次数 C o u n t Count Count 满足 C o u n t ≥ m Count \ge m Count≥m了,就返回假,否则为真。
附上贪心证明(Ta人博客,尽量点赞)。
AC Code
#include<bits/stdc++.h>
using namespace std;
char buf[1048576], *p1, *p2;
template<typename T>inline void Super_Quick_Read(T &x) {
bool f = 1;
x = 0;
char ch = (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? 0 : *p1++);
while (ch < '0' || ch > '9') {
if (ch == '-') f = !f;
ch = (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? 0 : *p1++);
}
while (ch >= '0' && ch <= '9')x = (x << 1) + (x << 3) + (ch ^ 48), ch = (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? 0 : *p1++);
x = (f ? x : -x);
return;
}
template<typename T>inline void Quick_Write(T x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) Quick_Write(x / 10);
putchar(x % 10 + '0');
return;
}
int n;
long long m, a[100001];
long long Tong[100001];
long long Answer;
inline bool Check(long long x) {
long long _count = 0;
for (register int i = 1; i <= n; ++i) Tong[i] = ceil(1.0 * x / a[i]);
for (register int i = 1; i <= n; ++i) {
if (Tong[i] <= 0) {
++_count;
continue;
}
_count += Tong[i] * 2 - 1, Tong[i + 1] -= Tong[i] - 1;
if (_count > m) return 0;
}
return 1;
}
signed main() {
int T;
Super_Quick_Read(T);
while (T--) {
Super_Quick_Read(n), Super_Quick_Read(m);
for (register int i = 1; i <= n; ++i) Super_Quick_Read(a[i]);
long long left = 0, right = LONG_LONG_MAX, middle;
while (left <= right) {
middle = (left + right) >> 1;
if (Check(middle)) left = middle + 1, Answer = middle;
else right = middle - 1;
}
Quick_Write(Answer), puts("");
}
return 0;
}
知道复制代码会 CE,为什么不自己写呢?