刷题日记:面试经典 150 题 DAY4
- 125. 验证回文串
- 28. 找出字符串中第一个匹配项的下标
- 151. 反转字符串中的单词
- 6. Z 字形变换
- 68. 文本左右对齐
125. 验证回文串
原题链接 125. 验证回文串
双指针,一前一后,遇到非数字字母跳过即可
class Solution {
public:
bool isPalindrome(string s) {
int i = 0, j = s.size()-1;
while(i < j) {
while(i<j && !isalnum(s[i])) i++;
while(i<j && !isalnum(s[j])) j--;
if(tolower(s[i]) != tolower(s[j])) {
return false;
}
i++, j--;
}
return true;
}
};
28. 找出字符串中第一个匹配项的下标
原题链接 28. 找出字符串中第一个匹配项的下标
子串匹配问题,有很多算法,其中最著名的是KMP算法,时间复杂度是
O
(
M
+
N
)
O(M+N)
O(M+N)。之前短暂的理解过,现在又不明白了。贴一个讲解 可能是全网最清晰的KMP算法讲解
理解不了就硬背
class Solution {
public:
int strStr(string haystack, string needle) {
int len_n = needle.size();
int next[len_n];
next[0] = -1;
for(int i = 1, j = -1;i < len_n;i++){
while(j > -1 && needle[i] != needle[j+1]) j = next[j];
if(needle[i] == needle[j+1]) j++;
next[i] = j;
}
for(int i = 0, j = -1;i < haystack.size();i++) {
while(j > -1 && haystack[i] != needle[j+1]) j = next[j];
if(haystack[i] == needle[j+1]) j++;
if(j == len_n-1) {
return i-len_n+1;
}
}
return -1;
}
};
找到一个好理解的Sunday算法
算法仍然包括两步:预处理和移动模式串
基本流程是:
- 左对齐,开始进行匹配
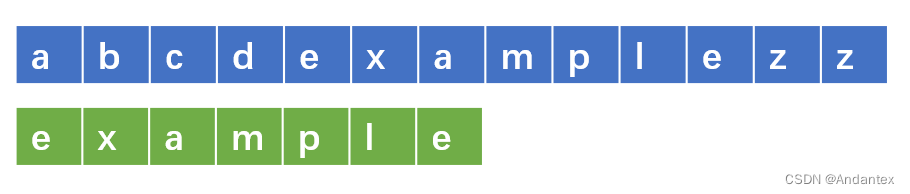
- 一旦匹配失败,对“下一位”进行检查
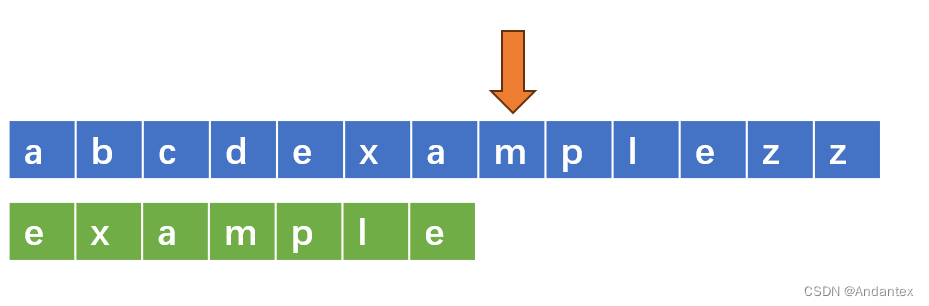
- 找到模式串中该字母最后出现的位置,然后对齐,开启下一轮匹配
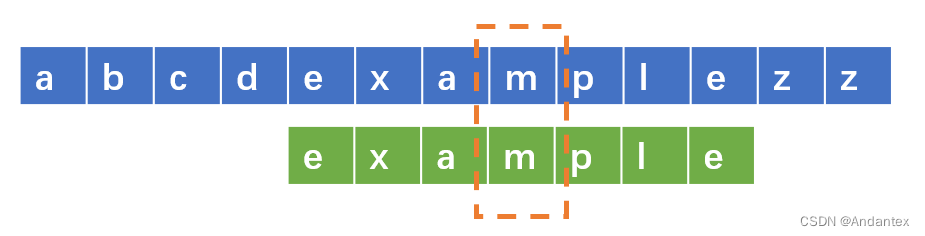
为了加速这个过程,我们预处理出一个键值对,键即字母表中的各个字母,对应的值是该字母在模式串中出现的位置(事实上,我们使用一个数组进行模拟;并且处理值,使得其意味着“此时模式串应该向后平移几位”)
class Solution {
public:
int strStr(string haystack, string needle) {
int n = haystack.size(), m = needle.size();
if(m > n) return -1;
vector<int> shifts(26,m+1);
for(int i = 0;i < m;i++) {
shifts[needle[i]-'a'] = m-i;
}
int s = 0, i;
while(s <= n-m) {
i = 0;
while(haystack[s+i] == needle[i]) {
i++;
if(i == m) {
return s;
}
}
if(s+m >= n) break;
s += shifts[haystack[s+m]-'a'];
}
return -1;
}
};
151. 反转字符串中的单词
原题链接 151. 反转字符串中的单词
- 第一步,去掉前后的空格
- 第二步,双指针,均从串末尾开始遍历,一个指向单词的开头,一个指向单词的结尾
- 交替地判断正在被遍历的是字母还是空格
class Solution {
public:
string reverseWords(string s) {
int i,j;
int len = s.size();
for(i = 0;i < len && s[i] == ' ';i++);
for(j = len-1;j >= 0 && s[j] == ' ';j--);
s = s.substr(i,j-i+1);
i = s.size()-1;
j = s.size()-1;
string result = "";
while(i >= 0) {
while(i >= 0 && s[i] != ' ') i--;
result += s.substr(i+1,j-i) + " ";
while(i >= 0 && s[i] == ' ') i--;
j = i;
}
result = result.substr(0,result.size()-1);
return result;
}
};
6. Z 字形变换
原题链接 6. Z 字形变换
直接分类讨论,设我们讨论在Z字形中的第i行第j个字母,其在原串中的位置是index
- 每一行的
index都从i开始 - 对于第一行和最后一行,
j每增加1,index增加2*(numRows-1) - 对于中间
j是偶数,则index增加2*(numRows-i-1)j是奇数,则index增加2*i
class Solution {
public:
string convert(string s, int numRows) {
int len = s.size();
if(numRows == 1 || len <= numRows) return s;
string result;
int t = 2*(numRows-1);
for(int i = 0;i < numRows;i++) {
int j = 0;
int index = i;
while(index < len) {
result.push_back(s[index]);
if(i == 0 || i == numRows-1) {
index += t;
} else if(j%2 == 0) {
index += t-2*i;
} else {
index += 2*i;
}
j++;
}
}
return result;
}
};
68. 文本左右对齐
原题链接 68. 文本左右对齐
做的我有点脑溢血了,大致分三步
- 第一步,将原单词列分成连续的区间,每个区间中的单词应该以左右对齐放在一行中
- 设单词数量是
n
n
n,单词总长度是
s
u
m
sum
sum,则满足
s
u
m
+
n
−
1
≤
m
a
x
W
i
d
t
h
sum+n-1 \leq maxWidth
sum+n−1≤maxWidth的尽可能长的一组单词应该放到一行(即,最少在每个单词之间放一个空格)
-
这一步我脑残突然发了,死活写不出来。其实简化一下问题就是:有一个数组,一个最大和maxSum。写一个函数,将数组分成几个尽可能长的连续片段,使得在每个连续片段内,数组元素的和都小于等于maxSum。代码应该是:
vector<vector<int>> splitArray(const vector<int>& nums, int maxSum) { vector<vector<int>> result; int currentSum = 0; vector<int> currentSegment; for (int num : nums) { if (currentSum + num > maxSum) { // 当前片段的和超过maxSum,将当前片段加入结果,并开始新的片段 result.push_back(currentSegment); currentSegment.clear(); currentSum = 0; } currentSegment.push_back(num); currentSum += num; } // 将最后一个片段加入结果 result.push_back(currentSegment); return result; }- 应该是 执行循环判断是否下标越界–>再循环内先判断是否已经超出最大和–>构造序列
-
- 设单词数量是
n
n
n,单词总长度是
s
u
m
sum
sum,则满足
s
u
m
+
n
−
1
≤
m
a
x
W
i
d
t
h
sum+n-1 \leq maxWidth
sum+n−1≤maxWidth的尽可能长的一组单词应该放到一行(即,最少在每个单词之间放一个空格)
- 第二步,对每组单词,执行左右对齐。假设需要 s s s个空格放到 n n n个间隔之中去,思路是先给每个间隔分配 ⌊ s n ⌋ \lfloor \frac{s}{n} \rfloor ⌊ns⌋个空格,再给前 s m o d n s \mod n smodn个间隔多分配上一个空格
- 第三步,给剩下的单词分配左对齐。这个好说。
class Solution {
public:
struct Line {
int st;
int ed;
int lw;
};
string space_factory(int n) {
return string(n,' ');
}
vector<string> fullJustify(vector<string>& words, int maxWidth) {
int len = words.size();
int wordsize[len];
for(int i = 0;i < len;i++) {
wordsize[i] = words[i].size();
}
vector<Line> lines;
int start = 0, count = 0, sum = 0;
while(start < len) {
count = 0;
sum = 0;
while(start+count < len) {
if(sum+count+wordsize[start+count]>maxWidth) {
lines.push_back({start,start+count-1,sum});
break;
}
sum += wordsize[start+count];
count++;
}
start += count;
}
start -= count;
vector<string> res;
for(int i = 0;i < lines.size();i++) {
auto line = lines[i];
int sum_spaces = maxWidth-line.lw;
string new_line = "";
new_line += words[line.st];
if(line.st == line.ed) {
new_line += space_factory(sum_spaces);
} else {
int sigle_spaces = (sum_spaces)/(line.ed-line.st);
int remain_spaces = (sum_spaces)%(line.ed-line.st);
for(int j = 1;line.st+j<=line.ed;j++) {
if(j-1 < remain_spaces) {
new_line += space_factory(sigle_spaces+1);
} else {
new_line += space_factory(sigle_spaces);
}
new_line += words[line.st+j];
}
}
res.push_back(new_line);
}
string new_line = "";
new_line += words[start];
sum = wordsize[start];
for(int i = start+1;i < len;i++) {
new_line += " ";
new_line += words[i];
sum += wordsize[i];
}
new_line += space_factory(maxWidth-sum-(len-start-1));
res.push_back(new_line);
return res;
}
};