有意向获取代码,请转文末观看代码获取方式~
展示出图效果

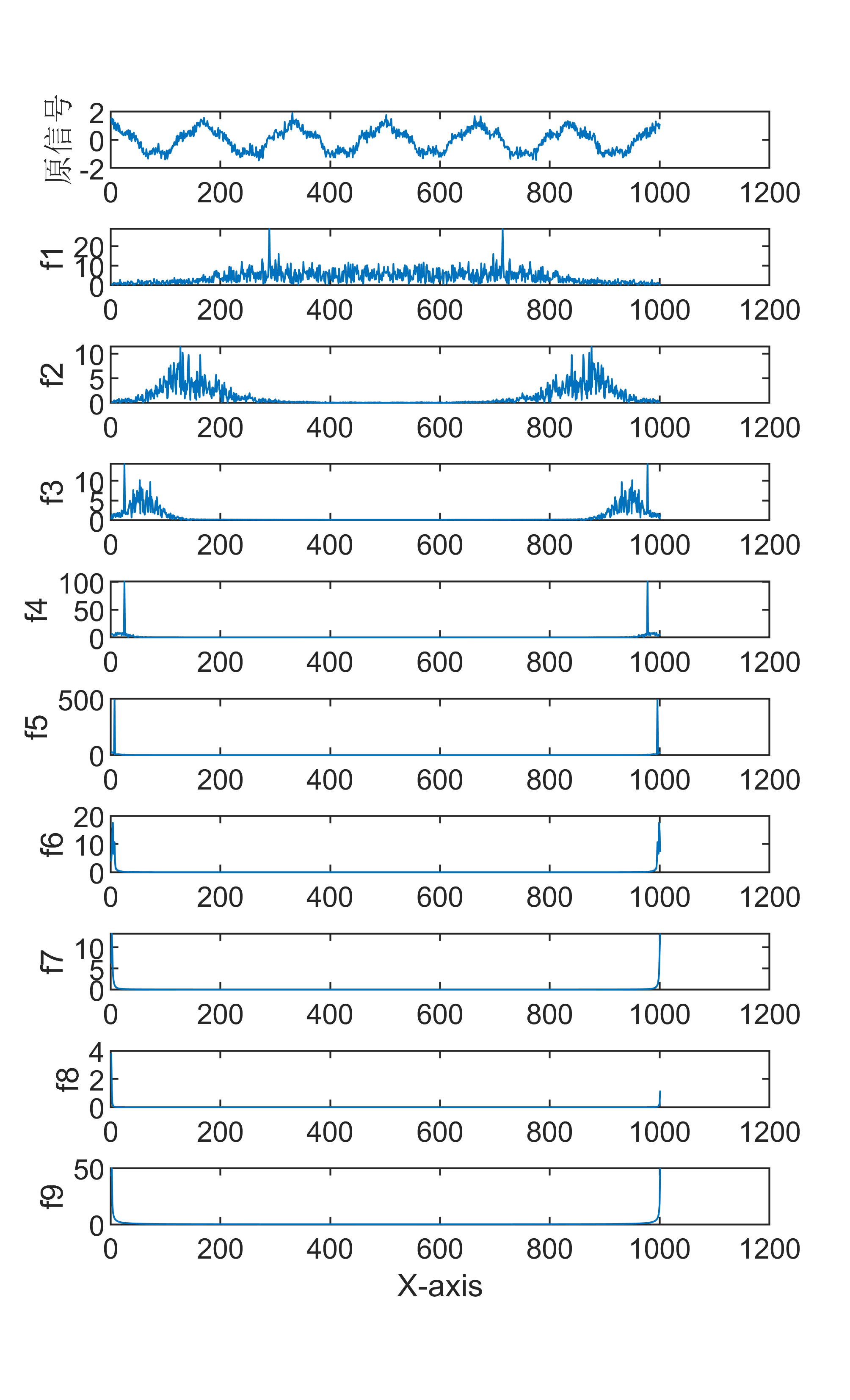
1 CEEMD信号分解算法
CEEMD 分解又叫互补集合经验模态分解,英文全称为 Complementary Ensemble Empirical Mode Decomposition。
CEEMD是对EEMD的改进,它在EEMD的基础上引入了一个自适应的扩展方法,可以更好地解决EMD/EEMD中存在的模态混叠问题。CEEMD的主要步骤如下:
-
对原始信号进行若干次随机噪声扰动,得到多个噪声扰动数据集。
-
对每个噪声扰动数据集进行EMD分解,得到多个EMD分解集合。
-
对于每个EMD分解集合,通过一个自适应的扩展方法,将每个局部模态函数分配到它所属的固有模态函数上,消除模态混叠的影响。
-
将每个扩展后的 EMD 分解集合的对应分量进行平均,得到最终的 CEEMD 分解结果。 CEEMD 分解具有良好的局部性和自适应性,能够更准确地分解信号,同时避免了 EEMD 中的模态混叠问题。因此,CEEMD 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。
要想在 MATLAB 中使用 EMD 分解首先要安装 EMD 分解的 MATLAB 工具包。
关于简短的代码视频教程均可关注B站、小红书、知乎同名账号(Lwcah)观看教程~
EMD 工具包的安装:在 MATLAB 打开 package_emd 文件夹,运行 install_emd. M 以及 index_emd. M 两个函数如下图所示即可完成工具包的安装。
MATLAB 信号分解第三期-CEEMD:
信号分解全家桶详情请参见:
2 FFT傅里叶频谱变换算法
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
MATLAB | 频谱分析算法 | 傅里叶变换 开源 MATLAB 代码请转:
MATLAB | 9种频谱分析算法全家桶详情请参见:
3 CEEMD信号分解+FFT傅里叶频谱变换组合算法
如下为简短的视频操作教程。
【MATLAB 】 CEEMD信号分解+FFT傅里叶频谱变换组合算法请转:
【MATLAB 】信号分解+FFT傅里叶频谱变换组合算法全家桶详情请参见:
关于代码有任何疑问,可以一起探讨科研,写作,代码等诸多学术问题,我们一起进步~
代码见附件~
![[HackMyVM]靶场 Wild](https://img-blog.csdnimg.cn/direct/b4c47be59eff48bd8e18ff09c60609e3.png)






![【二分查找】【map]436. 寻找右区间](https://img-blog.csdnimg.cn/f95ddae62a4e43a68295601c723f92fb.gif#pic_center)