我们今天继续来随机看5道AMC10真题,以及详细解析,这些题目来自1250道完整的官方历年AMC10真题库。通过系统研究和吃透AMC10的历年真题,参加AMC10的竞赛就能拿到好名次。
即使不参加AMC10竞赛,初中和高中数学一定会学得比较轻松、游刃有余。孩子学有余力的情况下,参加一下这个比赛也是激发兴趣和好胜心的一种方法,以赛促学。也是孩子宝贵的一种学习经历和见识。

为帮助大家,我整理了2000-2023年的全部AMC10的A卷和B卷的真题共1250题,并且独家制作了多种在线练习,利用碎片化时间,一年足以通过自学在2024年AMC10竞赛中取得好成绩。
2000-2023年AMC10真题练一练:2017年第15题

这道题的考点是概率(几何概型)。
因为两个人取值的变量是连续的。假设Chloe选的数是x,Laurent选的数是y,那么x和y的所有可能值组成的点对(x,y)形成一个矩形区域,如下图。y比x大的区域在y=x这根线上方,所以概率即为图中阴影部分占整个矩形区域的面积,计算结果为3/4,答案为C。
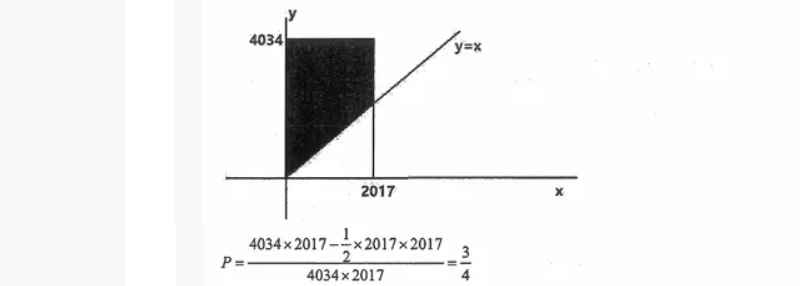
提醒:用几何概型解这类概率问题,将概率问题转化为面积占比的方法要掌握。
2000-2023年AMC10真题练一练:2016年第20题

这道题的考点是排列组合。结合多项式展开的通项定理和计算,解答过程如下:

2000-2023年AMC10真题练一练:2012年第10题

这道题的考点是数列(等差数列)。
假设最小的扇形角度为x度,则这些圆心角为x,x+d,x+2d,...x+11d.它们的和为360,即(x+x+11d)*12/2=360,即2x+11d=60,要使得x和d均为正整数,则d=2,x=19,或者d=4,x=8;因此x最小可能是8,答案为C。
2000-2023年AMC10真题练一练:2012年第13题

这道题的考点是代数,计算过程如下:

这道题难度不大,不过在实际比赛的时候有一些考生题目没有读懂,或者计算的时候粗心大意了失分。
2000-2023年AMC10真题练一练:2001年第9题

这道题的考点是代数(列方程解应用题)。
我们假设Kristin的年收入为S美元,根据题意得到如下方程:
S(p+0.25)/100=28000p/100+(p+2)(S-28000)/100。
化简得到,(P+0.25)S=28000p+Sp+2S-28000p-56000,即0.25S=2S-56000,解得,S=32000,答案为B。
从上面几道题我们发现,AMC10的题目有的时候相对长一点,列公式相对复杂一点,但是计算本身不难,所以要求我们读懂题目,计算过程更加细心。平时多练习刻意训练。
从1250道AMC10的真题研究来看,虽然AMC10是面向10年级(高一及以下)的数学竞赛,但是很多题目初中的知识就可以作答,甚至很多小学生参加过奥数的训练,或者AMC8的学习后也能作答大部分的AMC10的题目。
六分成长针对AMC10备考资源,欢迎了解更多

上述六分成长独家制作的在线练习题,符合学习和认知心理学,来源于完整的历年AMC8和AMC10真题,并且会持续更新。AMC8和AMC10备考可用,反复练习,也有利于小学、初中数学能力提升。








![[CSAWQual 2019]Web_Unagi ---不会编程的崽](https://img-blog.csdnimg.cn/direct/944a253cafd94adfbd956d3de7361107.png)