染色法：将图中所有的节点都染上颜色1或颜色2，染色规则为相邻节点不能为同一种颜色，即节点 x 若为颜色1则它的相邻节点 y 的颜色为2

时间复杂度：O(n+m)

解决问题：判断是否为二分图

二分图：又称作二部图，是图论中的一种特殊模型。图中的所有顶点可以分为两个集合，集合内部没有边存在，边只存在于集合之间，即所有边的顶点分别属于不同集合

二分图特性：二分图一定不含有奇数环

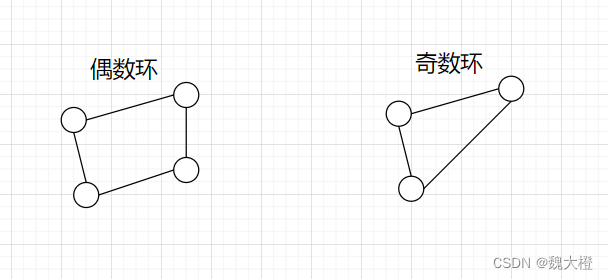
二分图只有偶数环，因为只有偶数环才可以保证成环的条件下还能保证在同一个集合内的环节点没有边存在，而奇数环的出现说明在这个环中至少有两个节点是在同一集合内，并且它们之间还存在边

示例代码：染色法判定二分图

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
//N点数，M边数；因为是无向图所以边数是点数的两倍
const int N = 100010,M = 200010;
//输入的点数、边数
int n,m;
//存储边的邻接矩阵
int h[N],e[M],ne[M],idx;
//存储边的染色情况，0为未染色，1为颜色1,2为颜色2
int color[N];

void add(int a,int b){
    ne[idx] = h[a];
    e[idx] = b;
    h[a] = idx;
    idx ++;
}

//深度遍历；参数（节点编号，颜色）
bool dfs(int u,int c){
    //染色
    color[u] = c;
    
    //遍历以节点u为起点的边
    for(int i = h[u] ; i != -1 ; i = ne[i]){
        int j = e[i];
        //未被染色，则进行以下操作
        if(!color[j]){
            //进行深度遍历染色递归操作
            if(!dfs(j,3-c)){
                //如果遍历结果为false则返回false；
                return false;
            }
        }
        //如果相邻节点染的颜色与本节点一致，则返回false
        else if(color[j] == c){
            return false;    
        }
    }
    return true;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    
    cin >> n >> m;
    memset(h,-1,sizeof h);
    int a,b;
    while(m--){
        cin >> a >> b;
        add(a,b),add(b,a);
    }
    
    bool flag = true;
    //遍历每个节点,对每个未染色的节点进行深度检查是否含有奇数环
    for(int i = 1 ; i <= n ; i++){
        //是否被染色，如果未被染色则进入语句
        if(!color[i]){
            //进行深度遍历，如果含有奇数环，dfs返回flag
            if(!dfs(i,1)){
                flag = false;
                break;
            } 
            
        }
    }
    
    if(flag){
        cout << "Yes" << endl;
    }else{
        cout << "No" << endl;
    }
    return 0;
}