前言
作者:小蜗牛向前冲
专栏:小蜗牛算法之路
专栏介绍:"蜗牛之道,攀登大厂高峰,让我们携手学习算法。在这个专栏中,将涵盖动态规划、贪心算法、回溯等高阶技巧,不定期为你奉上基础数据结构的精彩算法之旅。一同努力,追逐技术的星辰大海。"
目录
一、不同路径II(medium)
a、解题思路
b、代码
二、礼物的最⼤价值(medium)
a、解题思路
b、代码
三、 下降路径最⼩和(medium)
a、解题思路
b、代码
四、 最⼩路径和(medium)
a、解题思路
b、代码
五、地下城游戏(hard)
a、解题思路
b、代码
本期:继续手撕动态规划:不同路径II(medium),礼物的最⼤价值(medium),下降路径最⼩和(medium),最⼩路径和(medium),地下城游戏(hard)
继续刷动态规划相关算法题,如果不清楚什么是动态规划的可以看这里:[动态规划]---part1
一、不同路径II(medium)
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用
1和0来表示。示例 1:
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出:2 解释:3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有2条不同的路径: 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右示例 2:
输入:obstacleGrid = [[0,1],[0,0]] 输出:1提示:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]为0或1
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
}
};a、解题思路
这道题和同路径I的解题思路非常相似,但是就是在机器人找 到终点的过程中,会有障碍物。
1、转态表示
首先我们想以i,j位置为结尾表示什么
dp[i][j表示:以i,j位置结尾的时候,机器人到这里有多少条路径
2、状态转移方程
根据最近的一个位置划分:
当前位置有障碍物:
返回0
当前位置没有障碍物:
dp[i][j] = dp[i-1][j]+dp[i][j-1];

大家可能会想,我要是在[i-1][j]或者[i][j-1]遇到障碍物了,状态转态方程还可以相加吗?
其实是可能的,因为我在遇到障碍物是返回0的,而0对相加的结果是没有影响的。
3、初始化

这里我们要初始化,就是在二维数组多开一行和一列,但我们要思路多开的行列填什么呢(一切都是为了填表走服务)?,很明显,机器人是在[1,1]位置开始走的,也就说[1,1]位置肯定要为1(当最特色情况起点就是中点),所以我们只要保证,dp[1][0]==1或者dp[0][1]==1即可。其他位置看情况决定。
这里除了要注意填表的初始化,还要注意下标映射关心的改变:
obstacleGrid[0][0]-------->映射dp[1][1];
obstacleGrid[2][3]-------->映射dp[3][4];
也就是横着纵坐标都要加1
4、 填表顺序
从上往下填写每一行,每一行都是从左往又开始填写
5、返回值
dp[m][n]
b、代码
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid)
{
int m = obstacleGrid.size();//有多少行
int n = obstacleGrid[0].size();//有多少列
//创建dp表
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
//初始化
dp[1][0] = 1;
//填表
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (obstacleGrid[i - 1][j - 1] == 1)
{
dp[i][j] = 0;
}
else
{
dp[i][j] = dp[i][j - 1] + dp[i-1][j];
}
}
}
//返回
return dp[m][n];
}
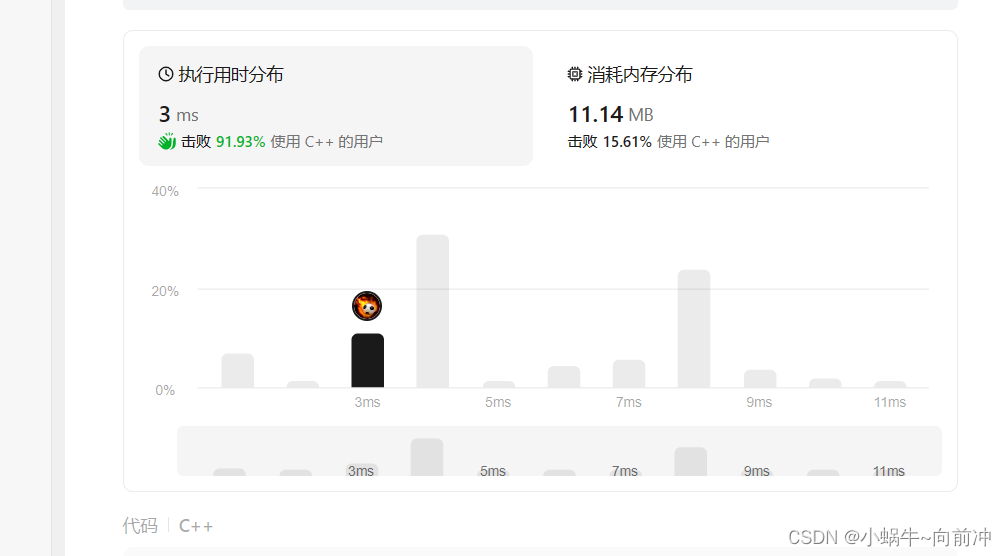
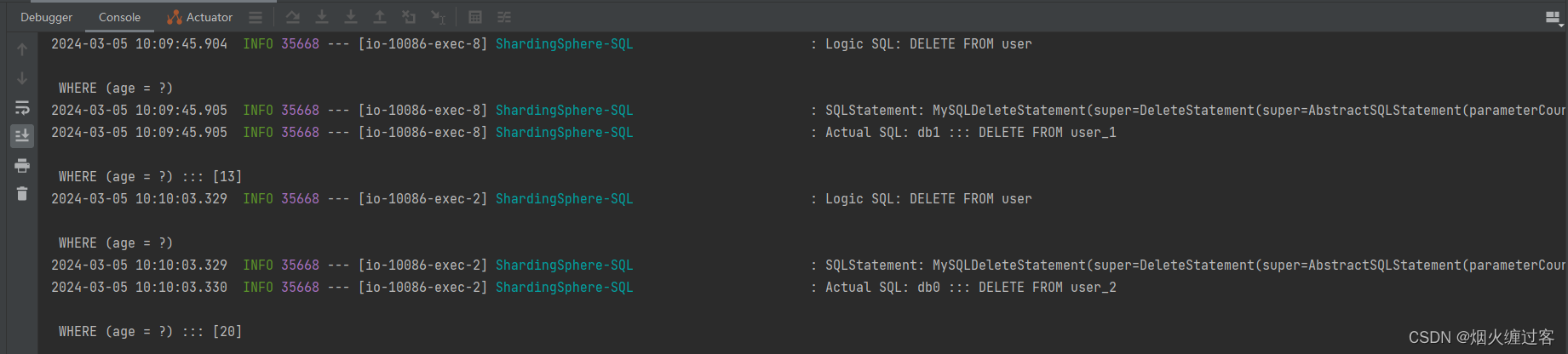
}; Leetcode 测试结果: 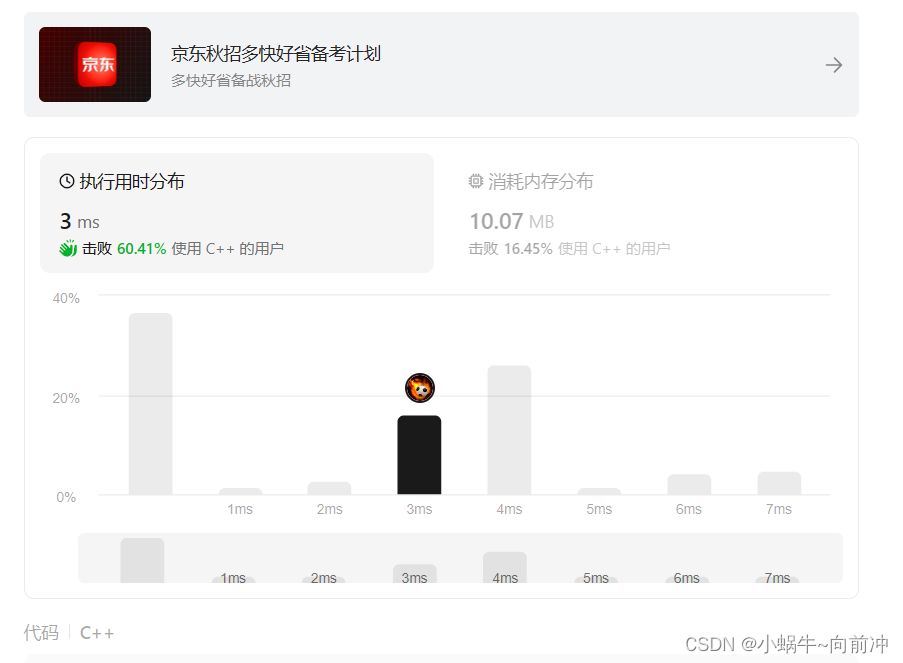
二、礼物的最⼤价值(medium)
现有一个记作二维矩阵
frame的珠宝架,其中frame[i][j]为该位置珠宝的价值。拿取珠宝的规则为:
- 只能从架子的左上角开始拿珠宝
- 每次可以移动到右侧或下侧的相邻位置
- 到达珠宝架子的右下角时,停止拿取
注意:珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝,比如
frame = [[0]]。示例 1:
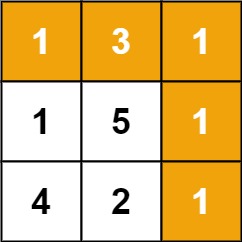
输入: frame = [[1,3,1],[1,5,1],[4,2,1]] 输出:12解释: 路径 1→3→5→2→1 可以拿到最高价值的珠宝提示:
0 < frame.length <= 2000 < frame[0].length <= 200
class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
}
};a、解题思路
这种路径题目极大可能用动态规划求解
1、转态表示
首先我们想以i,j位置为结尾表示什么
dp[i][j表示:以i,j位置结尾的时候,此时礼物的最大值
2、状态转移方程
根据最近的一个位置划分:
从[i-1][j]------>[i][j]:
那礼物的不就是dp[i-1][j]+frmae[i-1][j-1];(frmae的坐标是映射过的)
从[i][jj-1]------>[i][j]:
那礼物的不就是dp[i][j-1]+frmae[i-1][j-1];
但是我们要求的是拿到礼物的最大值:
状态转移方程:dp[i][jj = max(dp[i-1][j],dp[i][j-1])+frmae[i][j];
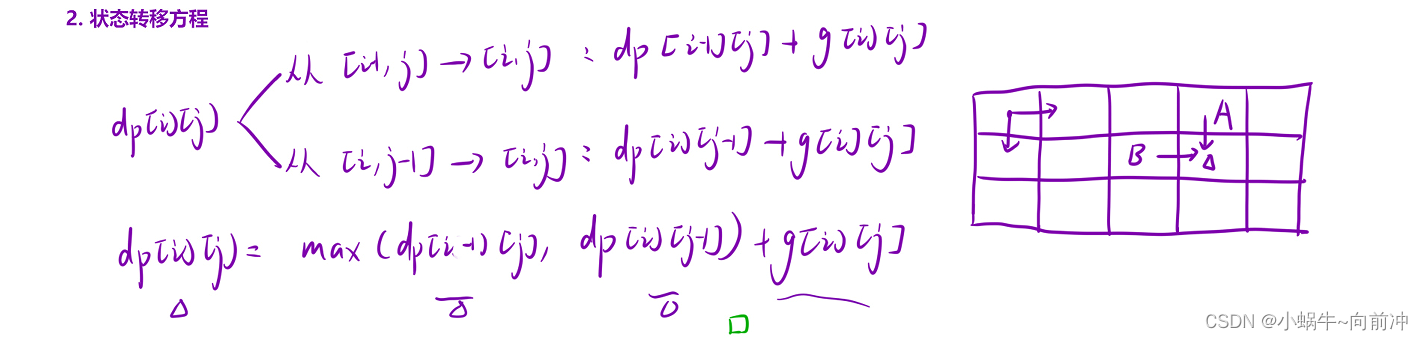
3、初始化

这里的初始化就非常简单了,对应[1][1]位置我们肯定是要保证他在填表的时候不变的,那么[1][0]和[0][1]位置肯定是0,至于0行,0列后面的,按理来说是要初始化为负无穷的,但因为礼物值>=0,所以初始化为0也可以。(这里就不用我们初始化了,因为vector是有初始化功能的)
4、 填表顺序
从上往下填写每一行,每一行都是从左往又开始填写
5、返回值
dp[m][n]
b、代码
class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame)
{
int m = frame.size();//行
int n = frame[0].size();//列
//创建dp表
vector<vector<int>> dp(m+1,vector<int>(n+1));
//初始化,vector已经完成
//填表
for(int i = 1;i<=m;i++)
{
for(int j = 1;j<=n;j++)
{
dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + frame[i-1][j-1];
}
}
return dp[m][n];
}
}; Leetcode 测试结果: 
三、 下降路径最⼩和(medium)
给你一个
n x n的 方形 整数数组matrix,请你找出并返回通过matrix的下降路径 的 最小和 。下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置
(row, col)的下一个元素应当是(row + 1, col - 1)、(row + 1, col)或者(row + 1, col + 1)。示例 1:
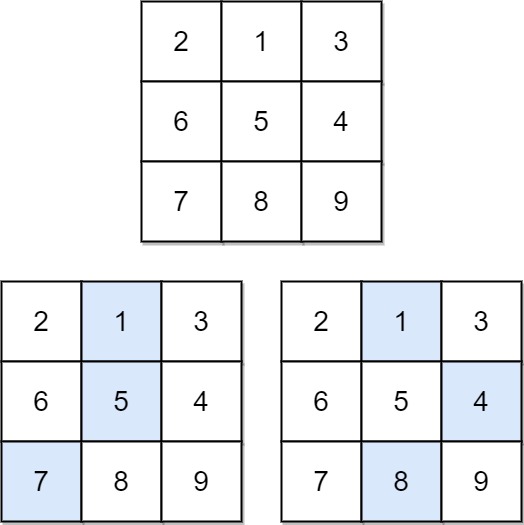
输入:matrix = [[2,1,3],[6,5,4],[7,8,9]] 输出:13 解释:如图所示,为和最小的两条下降路径示例 2:
输入:matrix = [[-19,57],[-40,-5]] 输出:-59 解释:如图所示,为和最小的下降路径提示:
n == matrix.length == matrix[i].length1 <= n <= 100-100 <= matrix[i][j] <= 100
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
}
};
a、解题思路
上面我们刚刚做完最大价值,现在来做最小和,二者思路非常相似,但是我们这里要仔细读题。
1、转态表示

dp[i][j]表示:到达[i,j]位置时,最小的下降路径
2、状态转移方程
根据最近的一个位置划分:
从[i-1][j-1]------>[i][j]:
那最小的下降路径不就是dp[i-1][j-1]+m[i][j;
从[i][jj-1]------>[i][j]:
那最小的下降路径不就是dp[i-1][j]+m[i][j;
从[i]-1[jj]------>[i][j]:
那最小的下降路径不就是dp[i-1][j+1]+m[i][j;
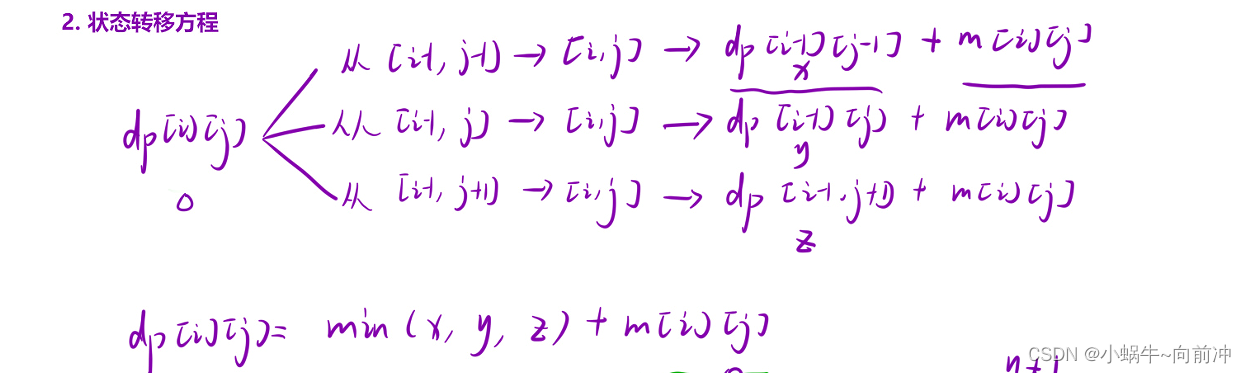
但是我们要求的是最小的下降路径
状态转移方程:dp[i][jj = min(x,y,z)+m[i][j];
3、初始化
这里的初始化和前面有点不同,所以我希望大家在做这种类型题目的时候,不要无脑初始化,一定要先进行分析。
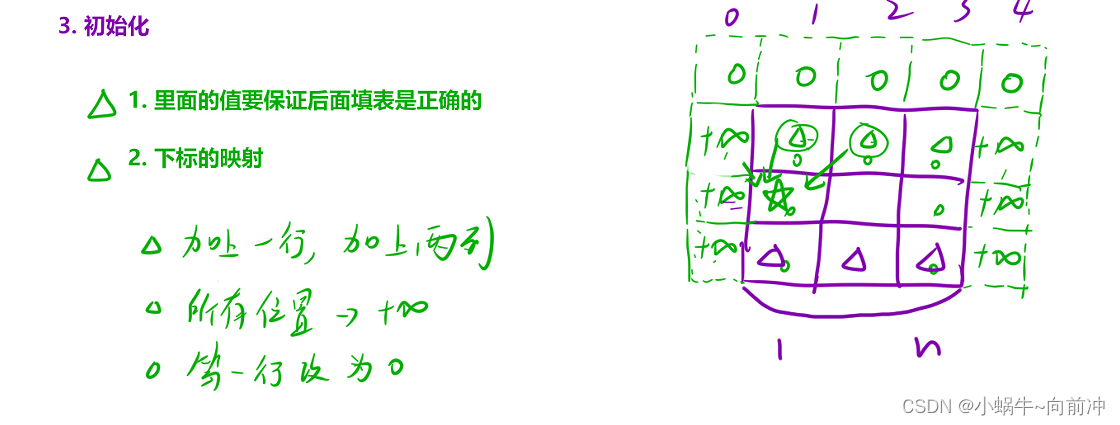
- 首先我们肯定是其想是第一行位置的值, 肯定是其本身(最小的下降路径),根据转态转移方程,我们肯定是不能让我们新添加的行影响结果,所以把第一行初始化为0。
- 在选择dp[1][2]进行观测(不一定非要选择这个位置,合适就好),根据转态转移方程,我们肯定是不能让我们新添加的列影响结果,所以要把第一列初始化为正无穷(第一行元素除外)
- 在选择dp[1][3]进行观察,,根据转态转移方程,我们肯定是不能让我们新添加的列影响结果所以要把最后一列初始化为正无穷(第一行元素除外)
4、 填表顺序
从上往下填写,值到最后一行
5、返回值
返回最后一行的最小值
b、代码
class Solution {
public:
int get_min(int x,int y,int z)
{
int tmp = min(x,y);
return min(tmp,z);
}
int minFallingPathSum(vector<vector<int>>& matrix)
{
int m = matrix.size();
int n = matrix[0].size();
int max = INT_MAX;//相当与正无穷
//创建dp表
vector<vector<int>> dp(m+1,vector<int>(n+2,max));
//初始化 这里初始化第一行就好
for(int i = 0;i<n+2;i++)
{
dp[0][i] = 0;
}
//填表
for(int i = 1;i<=m;i++)
{
for(int j =1;j<=n;j++)
{
dp[i][j] = get_min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+matrix[i-1][j-1];
}
}
//遍历最后一行找出最小值返回
int min = max;
for(int i = 1;i<=n;i++)
{
if(dp[m][i]<min) min = dp[m][i];
}
return min;
}
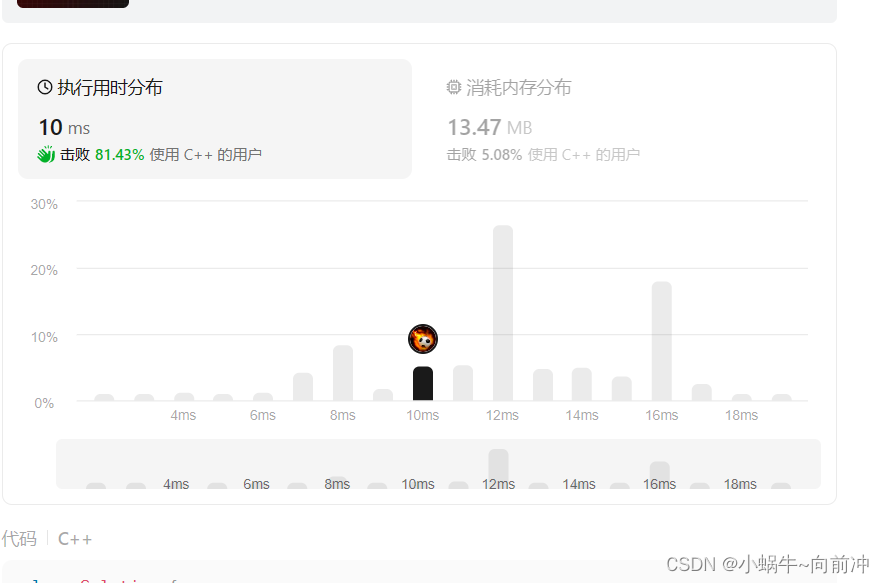
};Leetcode 测试结果:
四、 最⼩路径和(medium)
给定一个包含非负整数的
m x n网格grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。
示例 1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。示例 2:
输入:grid = [[1,2,3],[4,5,6]] 输出:12提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 200
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
}
};a、解题思路
又是这种路径的问题,我相信如果大家,认真做了前面的题,这题思路就非常清晰了
1、转态表示

dp[i][j]表示:到达[i,j]位置时,最小的路径路径和
2、状态转移方程
根据最近的一个位置划分:
从[i-1][j]------>[i][j]:
那最小路径和不就是dp[i-1][j]+g[i][j];
从[i][jj-1]------>[i][j]:
那最小的下降路径不就是dp[i][j-1]+g[i][j];
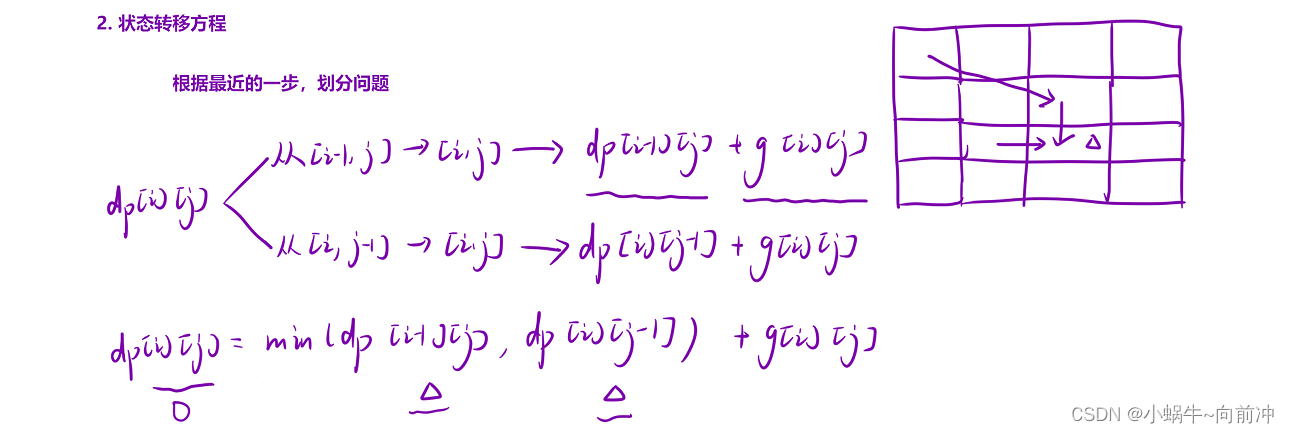
但是我们要求的是最小的下降路径
状态转移方程: dp[i][j] = min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
3、初始化
还先分析第一个位置,那么dp[0][1]和dp[1][0]就要初始化为0,其他位置,我们想现在可以总结一下了:
- 当求最小值 就初始化为正无尽
- 当求最大值 就初始化为负无尽
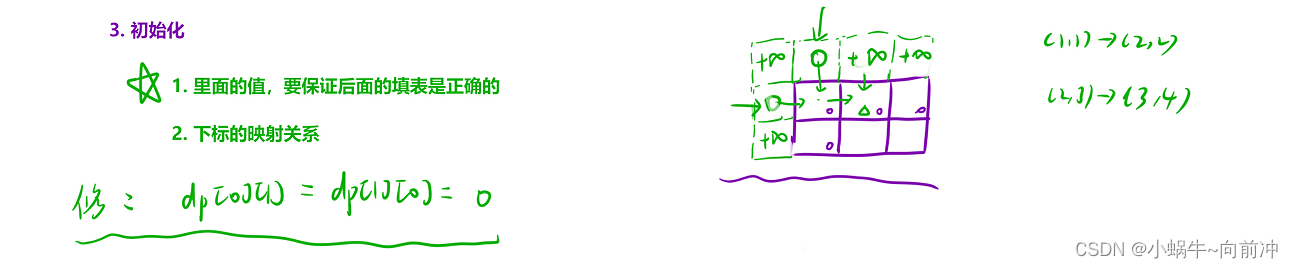
4、 填表顺序
从上往下填写,在从左往右。
5、返回值
dp[m][n]
b、代码
class Solution {
public:
int minPathSum(vector<vector<int>>& grid)
{
int m = grid.size();
int n = grid[0].size();
//创建dp
vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
//初始化
dp[1][0] = dp[0][1] = 0;
//填表
for(int i = 1;i<=m;i++)
{
for(int j = 1;j<=n;j++)
{
dp[i][j] = min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
}
}
//返回
return dp[m][n];
}
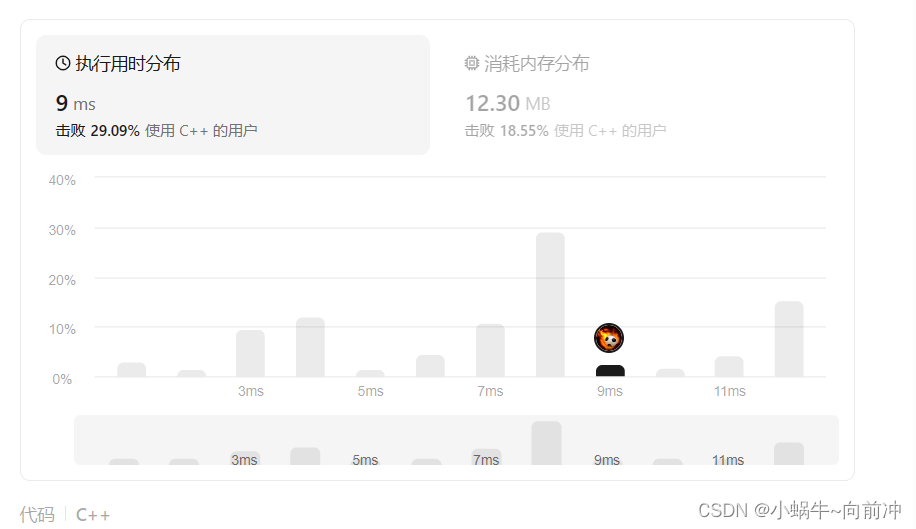
};Leetcode 测试结果:
五、地下城游戏(hard)
恶魔们抓住了公主并将她关在了地下城
dungeon的 右下角 。地下城是由m x n个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
示例 1:
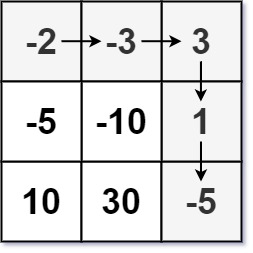
输入:dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]] 输出:7 解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。示例 2:
输入:dungeon = [[0]] 输出:1
class Solution {
public:
int calculateMinimumHP(vector<vector<int>>& dungeon) {
}
};a、解题思路
大家遇到这种文字多的题目,不要害怕,如果读不明白,就带这例题求推就好了。

1、转态表示

大家可能非常想到是以某一个位置结尾推出:
dp[i][j]表示:到达[i,j]位置时,所需的最低血量点数。但这是不正确的,因为我们不仅仅在[i][j]位置受到前面位置的影响,其实我们还会受到后面位置的影响,所以这样的转态表示是不可取的。
但是我们还可以想 一下以某位置为起点来推:
dp[i][j]表示从[i,j]位置重出发,到达终点所要的最低健康血量
2、状态转移方程
根据最近的一个位置划分:
往右走那最低血量应该是:dp[i][j+1] -d[i][j]
往下走那最低血量应该是:dp[i]+1[j] -d[i][j]
但是我们还要注意当d[i][j]此时非常大的时候,dp[i][j]可能出现负值,但是这样是不符合常理的,所以我们要处理一下:dp[i][j] = max(1,dp[i][j]);

,到达终点所要的最低健康血量
状态转移方程: dp[i][j] = min(dp[i][j+1],dp[i+1][j])+d[i][j];
3、初始化
这里我们填表因为是从后往前面填的,所以我们要关注最后一个位置,当我们救出公主的时候,肯定要保证自己的血量不为0,所以在[m][n-1]和[m-1][n]位置填1就好,其他位置为不影响 状态转移方程应该都初始化为正无穷。
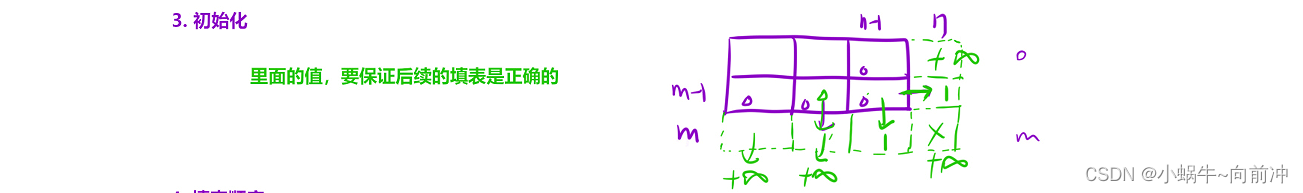
4、 填表顺序
从下往上填写,在从右往左。
5、返回值
dp[0][0]
b、代码
class Solution
{
public:
int calculateMinimumHP(vector<vector<int>>& dungeon)
{
int m = dungeon.size(), n = dungeon[0].size();
// 建表 + 初始化
vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
dp[m][n - 1] = dp[m - 1][n] = 1;
// 填表
for (int i = m - 1; i >= 0; i--)
for (int j = n - 1; j >= 0; j--)
{
dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
dp[i][j] = max(1, dp[i][j]);
}
// 返回结果
return dp[0][0];
}
};Leetcode 测试结果: