文章目录
- 一、概述
- 二、图像处理基础
- 2.1 视觉感知要素
- 2.2 像素间的一些基本关系
- 2.2.1 相邻像素
- 2.2.2 连通性
- 2.2.3 距离度量
- 2.3 基本坐标变换
- 2.4 空间变换与灰度值
一、概述
1. 图像的概念及分类。
图像是用各种观测系统以不同形式和手段观测客观世界而获得的、可以直接或间接作用于人的视觉系统而产生的视知觉实体。
图像分为模拟图像和数字图像:(1) 模拟图像:二维空间和亮度都是连续值的图像。亮度值连续且不分等级。 (2) 数字图像:二维空间和亮度都是用有限数字数值表示的图像。
2. 像素表示的矩阵、矢量形式。
一幅图像可分解为许多个单元。每个基本单元叫做图像元素,简称像素。

3. 图像工程的三个层次。

二、图像处理基础
2.1 视觉感知要素
1. 亮度适应与辨别:
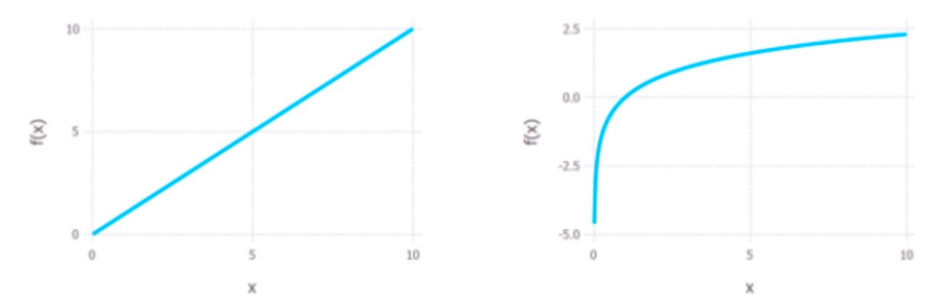
(1) 主观亮度:即人眼感知到的亮度,是进入人眼的光强的对数函数。
(2) 亮度适应现象:感知亮度不是亮度的简单函数。① 马赫带:视觉系统往往会在不同强度区域的边界处出现“ 下冲”或“上冲”现象(毛边)。② 同时对比:感知区域的亮度与背景亮度相关。
2. 当在白天进入一个黑暗剧场时,在能看清并找到空座位时需要适应一段时间,试述发 生这种现象的视觉原理?
答:人的视觉绝对不能同时在整个亮度适应范围工作,它是利用改变其亮度适应级来完成亮度适应的,即所谓的亮度适应范围。同整个亮度适应范围相比,能同时鉴别的光强度级的总范围很小。因此,白天进入黑暗剧场时,人的视觉系统需要改变亮度适应级,因此,需要适应一段时间,亮度适应级才能被改变。
2.2 像素间的一些基本关系
2.2.1 相邻像素
1. 相邻像素:4邻域、D邻域、8邻域。
2. 4邻域:像素 p ( x , y ) p(x,y) p(x,y) 的4邻域是 (x+1,y);(x-1,y);(x,y+1);(x,y-1)。用 N 4 ( p ) N_4(p) N4(p) 表示像素 p p p 的4邻域。

3. D邻域:像素 p ( x , y ) p (x,y) p(x,y) 的D邻域是对角上的点 (x+1,y+1);(x+1,y-1);(x-1,y+1);(x-1,y-1)。用 N D ( p ) N_D(p) ND(p) 表示像素 p p p 的D邻域。

4. 8邻域:像素 p ( x , y ) p(x,y) p(x,y) 的8邻域是4邻域的点+D邻域的点。用 N 8 ( p ) N_8(p) N8(p) 表示像素 p p p 的8邻域,即 N 8 ( p ) = N 4 ( p ) + N D ( p ) N_8(p)=N_4(p)+N_D(p) N8(p)=N4(p)+ND(p)。

2.2.2 连通性
1. 两个像素连通的两个必要条件是:两个像素的位置是否相邻;两个像素的灰度值是否满足特定的相 似性准则(或者是否相等)。
2. 4连通:对于具有值 V V V 的像素 p p p 和 q q q,如果 q q q 在集合 N 4 ( p ) N_4(p) N4(p) 中, 则称这两个像素是4连通的。

3. 8连通:对于具有值 V V V 的像素 p p p 和 q q q,如果 q q q 在集合 N 8 ( p ) N_8(p) N8(p) 中, 则称这两个像素是8连通的。

4. 对于具有值 V V V 的像素 p p p 和 q q q,如果: q q q 在集合 N 4 ( p ) N_4(p) N4(p) 中;或 q q q 在集合 N D ( p ) N_D(p) ND(p) 中,并且 N 4 ( p ) N_4(p) N4(p) 与 N 4 ( q ) N_4(q) N4(q) 的交集为空(没有值V的像素)则称这两个像素是m连通的。

5. 通路的定义:一条从具有坐标 ( x , y ) (x,y) (x,y) 的像素 p p p,到具有坐标 ( s , t ) (s,t) (s,t) 的像素 q q q 的通路,是具有坐标 ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_0,y_0),(x_1,y_1),...,(x_n,y_n) (x0,y0),(x1,y1),...,(xn,yn) 的不同像素的序列。其中, ( x 0 , y 0 ) = ( x , y ) (x_0,y_0)=(x,y) (x0,y0)=(x,y), ( x n , y n ) = ( s , t ) (x_n,y_n)=(s,t) (xn,yn)=(s,t), ( x i , y i ) (x_i,y_i) (xi,yi) 和 ( x i − 1 , y i − 1 ) (x_{i-1},y_{i-1}) (xi−1,yi−1) 是邻接的, 1 ≤ i ≤ n 1 ≤ i ≤ n 1≤i≤n, n n n 是路径的长度。如果 ( x 0 , y 0 ) = ( x n , y n ) (x_0,y_0)=(x_n,y_n) (x0,y0)=(xn,yn),则该通路是闭合通路。

2.2.3 距离度量
1. 基本定义如下:


2. 一道例题如下,通过上面的公式可以解决下面题目中的距离问题。


2.3 基本坐标变换
1. 坐标变换可借助矩阵写为: v ′ = T v v' =Tv v′=Tv

2. 例子:先放大2倍,然后旋转45度,然后再缩小0.5倍。

3. 平移变换并不是矩阵乘法的形式,而是矩阵加法的形式。

4. 改变图像的像素值,我们称为滤波(Filtering)。改变图像的像素位置,我们称为扭曲(Warping)。

5. 转置变换:图像转置是指将图像像素的x坐标和y坐标互换。图像的大小会随之改变,高度和宽度将互换。

6. 尺度变换(放缩变换):

7. 旋转变换矩阵:

2.4 空间变换与灰度值
1. 几何变换可在一幅图像中的像素间修改空间联系。几何变换通常又叫做橡皮片变换,因为它们可以被看做在一片橡皮片上打印图像,然后根据预先确定的规则拉伸这个橡皮片的过程。
2. 在数字图像处理中,几何变换由两个基本操作组成:空间变换,它定义了图像平面上像素的重新安排;灰度级插补,处理空间变换后图像中像素灰度级的赋值。
3. 空间变换:图显示了在失真和相应的校正图像中的四边形区域,四边的顶点是相应的 “连接点”。
4. 灰度级插补:图像经几何位置校正后,在校正空间中各像点的灰度值等于被校正图像对应点的灰度值。一般校正后的图像某些像素点可能挤压在一起,或者分散开,不会恰好落在坐标点上,因此常采用内插法来求得这些像素点的灰度值。
常用的有:最邻近插值法、双线性插值法(一阶插值)、高阶插值法。
5. 最近邻插值法:计算与点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0) 临近的四个点,将与点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0) 最近的整数坐标点 ( x , y ) (x,y) (x,y) 的灰度值取为 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0) 点灰度近似值。

6. 线性插值法:

7. 三阶插值:是指用 ( x , y ) (x ,y) (x,y) 周围的16个网格点灰度按三次多项式进行内插的高精度算法。

8. 常用的灰度插值有几种,概括它们的优缺点:
- 最邻近插值法, 这种方法简单但效果不太好。
- 双线性插值(一阶插值):计算量大,但缩放后图像质量高,不会出现图像不连续的情况。
- 高阶插值:计算量最大,插值后图像的视觉质量最好。