目录
题目:
DP分析:
代码:
3.6更新 贪心 第一个思考方式
先上代码:
解析:
贪心 第二个思考方式 (与上面的思路差不多,但是换了个角度)
思路:
代码:
所有的思路很重要!!!
题目:
给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数 N。
第二行包含 N 个整数,表示完整序列。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N≤1000,
−10^9≤数列中的数≤10^9输入样例:
7 3 1 2 1 8 5 6输出样例:
4
DP分析:
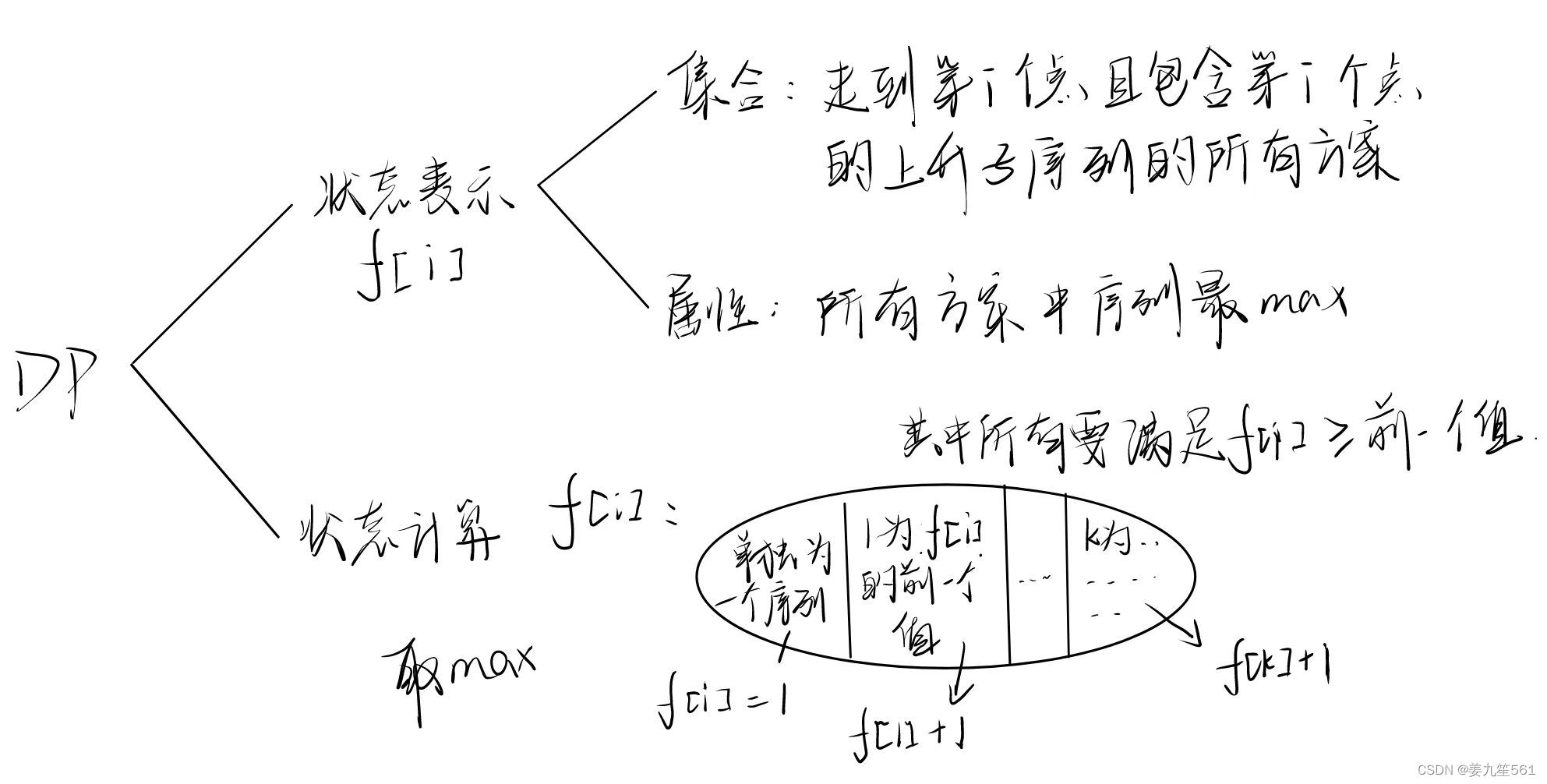
代码:
import java.io.*;
import java.util.*;
class Main{
static int N = 1010;
static int[] w = new int[N];
static int[] f = new int[N];
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(in.readLine());
String[] s = in.readLine().split(" ");
for(int i=1;i<=n;i++){
w[i] = Integer.parseInt(s[i-1]);
}
// DP
for(int i=1;i<=n;i++){
f[i] = 1; // 只有自身
for(int j=1;j<i;j++){
if(w[j]<w[i]) // 保证序列单调上升
f[i] = Math.max(f[i],f[j]+1);
}
}
// 不一定f[n]就是最长的,因为f[n]必定包含w[n]这个数,最长上升子序列可能不包含w[n]
int res = 0;
for(int i=1;i<=n;i++) res = Math.max(res,f[i]);
System.out.println(res);
}
}PS:
本来想尝试单调栈的。发现比如 3 1 2 1 8 5 6 。栈会删去 2 ,存进 1。而最长上升子序列为 1 2 5 6。
3.6更新 贪心 第一个思考方式
上面说到不可以使用单调栈。并且使用上面的代码,时间复杂度是O(n^2),如果N增大,就会超时。
单调栈:单调栈(思路+示例)-CSDN博客
但是参考了一篇大佬的代码 AcWing 896. 最长上升子序列 II - AcWing 我悟了。
先上代码:
// 类似于单调栈的做法,但是更多的有贪心的思想在。
// 替换掉第一个大于等于该值的在栈中的元素,目的是保证可以最大限度的增加上升子序列的长度。
/* ex:3 1 2 1 8 5 6
使用st[]存储值
i = 1, st[] = {3}
i = 2, st[] = {1}
i = 3, st[] = {1,2}
i = 4, st[] = {1,2} 此时这个1是被w[4]替换掉w[2]的1
i = 5, st[] = {1,2,8}
i = 6, st[] = {1,2,5}
i = 7, st[] = {1,2,5,6}
*/
import java.io.*;
import java.util.*;
class Main{
static int N = 100010;
static int[] w = new int[N];
static int[] st = new int[N]; // 单调栈
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(in.readLine());
String[] s = in.readLine().split(" ");
for(int i=1;i<=n;i++){
w[i] = Integer.parseInt(s[i-1]);
}
int res = 0;
int tt = 0; // 栈顶
for(int i=1;i<=n;i++){
if(tt==0||w[i]>st[tt]){ // 如果栈中没有值或者当前值大于栈顶元素,加入进去
st[++tt] = w[i];
res = Math.max(res,tt);
}
else{ // 否则,替换掉第一个大于等于该值的在栈中的元素
int idx = tt;
while(idx>0&&w[i]<=st[idx])
idx--;
st[idx+1] = w[i];
}
}
System.out.println(res);
}
}解析:
使用了单调栈+贪心的思想。
如果当前该值 大于栈顶元素,就加入栈
进去。
否则,找到栈中第一个大于等于 的值,用
替换掉该值。
(用二分,虽然这个代码没用)
ex:
疑惑:
- 一般的单调栈会将第
步的时候,删去
,再将
装入进去,但是会缩短上升子序列的长度。并且在
步的时候,数字
被保留了下来,没有被去除换成
。
- 最后的序列为
,而准确的最长上升子序列应该是
,这是为什么。
第一个问题:为什么有这种替换操作?主要是贪心,我们并不想在求解的过程中导致最长上升子序列越算越短。因此,如果我们目前算出的结果还没以前的长,会暂时保留以前的结果,当然也不丢弃目前的结果,因为之后继续计算的话,目前的结果可能更优。
为了实现上述目的,我们可以用新序列从左到右逐渐覆盖掉旧序列。当新序列长度 <原序列长度时,原序列没有被完全覆盖,因此保证长度不减小;当新序列长度 ≥原序列长度时,原序列已经被完全覆盖,现在就是以新序列为基础进行计算了。
因此就产生了这种特殊的替换方式。
第二个问题:最后的最长上升子序列不是准确的?因为由于贪心的思想,存在这种替换方式,导致最长上升子序列中某些值被替换掉,但是上升子序列的长度没有发生改变,只有里面的值发生了变化,因此,在求解该题中最长上升子序列的长度时可以被使用,但是要输出最长上升子序列的值的时候,就不行了。
核心就是因为栈中储存的不只有一个序列,是旧序列和新序列合并的产物,因此不一定是最终最长上升子序列。
贪心 第二个思考方式 (与上面的思路差不多,但是换了个角度)
思路:
换一种思路思考贪心的问题,如果我们要将 作为上升子序列的末尾元素。那么我们可以设计一个数组
,存储当上升子序列长度分别为
的时候最小的末尾值,其中,末尾值都是跟随数组下标的上升而严格上升的。
如果想要将 装入到序列中,我们只需要在长度为
中找到大于等于
的第一个末尾值
,此时
。此时我们将
装入到
的末尾,此时,序列的长度就增加了1,因此就要更新
的末尾值为
(这个操作就跟上面那种方法替换大于等于
的第一个值思路一样),从而保证了序列中的值尽可能小来增加最长子序列的可能性。
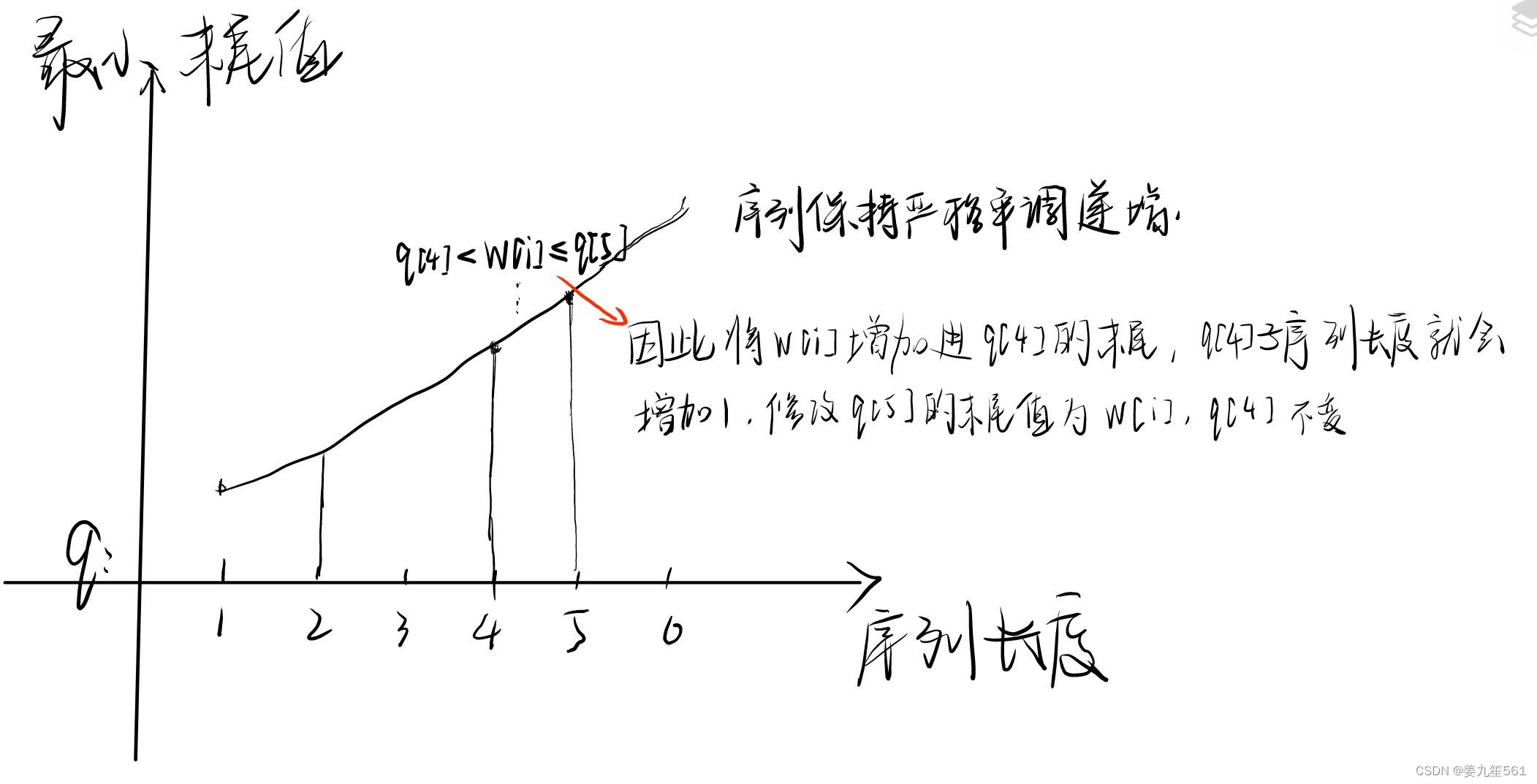
因为数组 中的值是严格单调递增的,因此可以使用二分来找到该
点。
代码:
import java.io.*;
import java.util.*;
class Main{
static int N = 100010;
static int[] w = new int[N];
static int[] q = new int[N]; // 存储每个上升子序列长度的最小末尾值
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(in.readLine());
String[] s = in.readLine().split(" ");
for(int i=1;i<=n;i++){
w[i] = Integer.parseInt(s[i-1]);
}
int len = 0; // q数组的长度
for(int i=1;i<=n;i++){
int l = 0, r = len; // l只能从0开始,因为存值的时候要+1
while(l<r){ // 找到q[l]<w[i]<=q[l+1] 的l点
int mid = l+r+1>>1;
if(q[mid]<w[i]) l = mid;
else r = mid-1;
}
q[r+1] = w[i]; // 更新l+1的末尾值
len = Math.max(len,r+1); // 取当前数组q和更新的数组q长度的最大值
}
System.out.println(len);
}
}