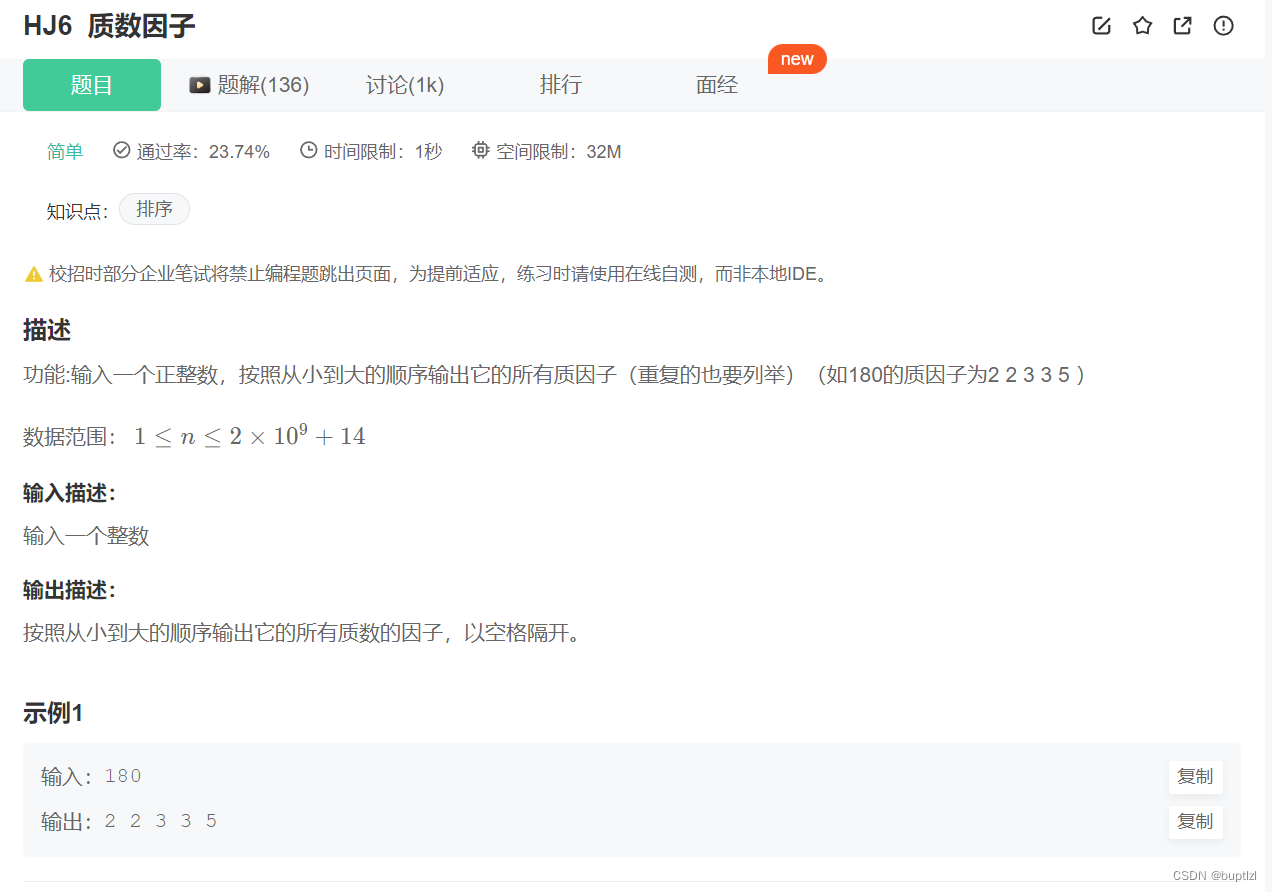
本题是要求一个数的所有质因子，包括重复的，比如180。首先质数就是素数，其只能被1和其本身整除（1不是质数）。比如2的因子只有1和2，3的因子只有1和3，5的因子只有1和5。
比如题中的180，能被2整除，得到90，再被2整除得到45，再被3整除得到15，再被3整除得到5，最后5是质数，所以结果就是2 2 3 3 5
本题中，我们不需要遍历到这个正整数，只需要到这个数的平方根就好，因为一个数的平方根乘以平方根等于这个数，这个数的因子一定有一个比平方根小，另一个比平方根大。而质因子一定是那个小的，因为大的可能有其他的因子。
所以我们首先从2开始遍历，如果能整除说明2是质因子，这时候我们要把i减去1，防止漏掉重复的质因子，比如180的2和3，都是重复的。如果我们遍历到正整数的平方根，则直接将这个正整数返回就好，说明它没有其他的质因子了，只有它本身。比如7，它的平方根比2大，比3小，当到2的时候不能够整除，到3的时候已经比他的平方根要大了，直接返回7就好，它的质因子只有它的本身。

import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = (int) Math.sqrt(m);//算术平方根函数
        for (int i = 2; i <= m; i++) {
            if (m % i == 0) {
                System.out.print(i + " ");
                m = m / i;
                i--;//避免遗漏重复的质数因子
            } else {
                if (i >= n) {
                    System.out.print(m + "");
                    break;
                }
            }
        }
    }
}