信息熵
信息量
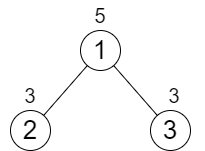
信息量是对信息的度量,衡量事件的不确定性,越小概率的事件发生了产生的信息量越大。我们应该用什么形式的函数表达信息量呢?除了随着概率增大而减少,这个函数还有具有以下性质:
如果有两个事件x和y彼此独立,那么:
并且,x和y同时发生时我们获得的信息应该等于这两个事件分别发生时我们获得的信息之和:
不难看出,H(x)应该与对数有关。因为我们将信息量定义为如下公式:
![]()
负号是为了确保信息一定是正数或者0,底数是任意的,底数为2时表示编码信息所需要的最少二进制位个数bits。
信息熵
信息量度量的是一个事件发生了所带来的信息,而信息熵是在结果出来之前对所有可能产生的信息量的期望——考虑随机变量的所有可能取值,即事件的所有可能性所带来的信息量的期望。简言之,熵是信息量的期望。

其中 代表随机事件X为
的概率
K-L散度 Kullback-Leibler Divergence(相对熵)
K-L散度用来衡量两个分布对于同一变量的差异情况。在概率学中,我们经常使用更简单的分布来近似观察数据或复杂分布。K-L散度能帮助我们度量使用一种分布近似另一种分布时所损失的信息量。设p为观察得到的概率分布,q为另一分布来近似p,则p、q的K-L散度为:
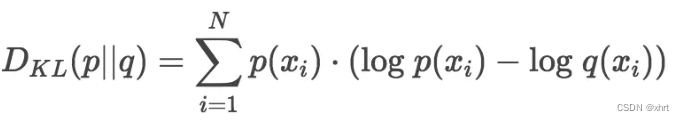
显然,根据上述公式,K-L散度其实是统一随机变量x的原始分布p和近似分布q之间的对数差值的期望。如果继续用2为底的对数计算,则K-L散度值表示信息损失的二进制位数。K-L散度通常也被写为以下形式:
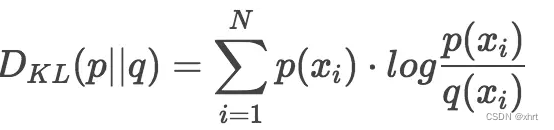
散度并非距离
有人把K-L散度看做不同分布之间距离的度量,这是不对的,因为K-L散度不满足对称性。也就是说,用p近似q和用q近似p,二者所损失的信息是不一样的。
交叉熵
交叉熵,用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。这也是为什么在机器学习分类算法中,我们总是最小化交叉熵,因为交叉熵越低,就证明由算法所产生的策略最接近最优策略,也间接证明我们算法所算出的非真实分布越接近真实分布。而KL散度(相对熵),是用来衡量不同策略之间的差异的。
我们将KL散度公式变形:

等式的前一部分恰巧就是p的熵,等式的后一部分,就是交叉熵:
![]()
在机器学习中,我们需要评估label和predicts之间的差距,使用KL散度刚刚好,即 ,由于KL散度中的前一部分−H(y)不变,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss,评估模型。
互信息MI
互信息(Mutual Information)度量两个随机变量共享的信息——知道随机变量X,随机变量Y不确定性减小的程度(或者知道随机变量Y,随机变量X不确定性减小的程度),用I(x;y)表示。
举例来说,随机变量X表示一个均衡的六面骰子投掷出的点数,Y表示X的奇偶性。这里我们设X是偶数时,Y=0;X是奇数时,Y=1。如果我们知道X,如X=1,则可以判断Y=1。(失去Y=0这一信息的可能性,Y的不确定性信息减少了)。同样的,如果我们知道Y=0,则可以判断X=2或4或6。(失去X=1或3或5这一信息的可能性,X的不确定性信息减少了)因此,我们说随机变量X和Y之间存在互信息。
我们可以通过下面这张互信息的韦恩图来形象的理解互信息和熵的关系与区别:

关于这张图的理解:

最后,我们通过一系列的数学公式的推导,得到以下互信息的定义式:
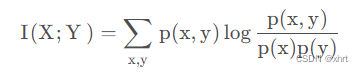
点互信息(PMI)
点互信息(Pointwise Mutual Information),衡量两个事物之间的相关性,比如两个单词。

如果x和y相互独立,则,此时PMI为0,其计算过程如下:

如果x和y的出现不是独立事件,即某个字的出现会提升另一个字出现的概率,那么PMI大于0,其计算过程如下:
![]()
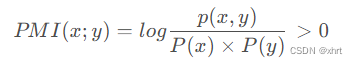
但是由于log0=-inf,即负无穷。为此,我们通常使用PPMI(Positive PMI)来避免出现-inf,即:

回顾互信息的计算公式为:
![]()
衡量的是两个随机变量的相关性,即一个随机变量中包含另一个随机变量的信息量。
可以看出,互信息其实就是对X和Y的所有可能取值的点互信息的加权和。
参考链接:
通俗理解信息熵 - 知乎
如何理解K-L散度(相对熵) - 简书
如何通俗的解释交叉熵与相对熵? - 知乎
特征选择之互信息(mutual information)算法思想及其python代码实现_mutual_info_score-CSDN博客
[DataAnalysis]点互信息_点的互信息-CSDN博客
NLP之【点互信息PMI】——衡量两变量之间的相关性_点互信息(pmi)-CSDN博客