2673. 使二叉树所有路径值相等的最小代价
给你一个整数n表示一棵 满二叉树 里面节点的数目,节点编号从1到n。根节点编号为1,树中每个非叶子节点i都有两个孩子,分别是左孩子2 * i和右孩子2 * i + 1。
树中每个节点都有一个值,用下标从0开始、长度为n的整数数组cost表示,其中 cost[i]是第i + 1个节点的值。每次操作,你可以将树中 **任意** 节点的值 增加 1` 。你可以执行操作 任意 次。
你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。
注意:
满二叉树 指的是一棵树,它满足树中除了叶子节点外每个节点都恰好有 2 个子节点,且所有叶子节点距离根节点距离相同。
路径值 指的是路径上所有节点的值之和。
示例 1:
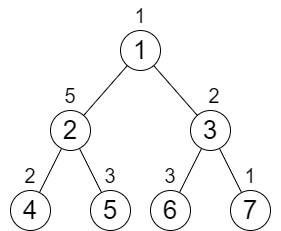
输入:n = 7, cost = [1,5,2,2,3,3,1]
输出:6
解释:我们执行以下的增加操作:
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。
示例 2:
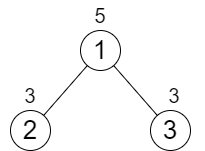
输入:n = 3, cost = [5,3,3]
输出:0
解释:两条路径已经有相等的路径值,所以不需要执行任何增加操作。
题目分析
贪心算法是一种基于贪心策略的算法设计方法,用于在求解最优化问题时作出一系列局部最优选择,从而达到全局最优的目标。贪心算法通常适用于满足最优子结构性质的问题,即问题的最优解可以通过一系列局部最优解的组合来得到
对于任一叶结点,它的值为 x,它的兄弟节点的值为 y,要想使得根到这两个叶节点的路径值相等,我们只能增加 x 和 y 本身。
由于我们希望操作次数最少,那么应该进行 ∣x−y∣ 次操作,将较小的值增加至与较大的值相等。
待考虑完所有叶节点之后,互为兄弟节点的叶节点的值两两相等(并且根到它们的路径值显然也相等)。如果我们还需要操作某个叶节点,那么为了使得路径值相等,它的兄弟节点同样也需要操作。此时就需要两次操作,但不如直接操作它们的双亲节点,可以省去一次操作。
因此,所有的叶节点都无需进行操作。我们就可以将它们全部移除。为了使得路径值保持不变,我们可以将叶节点的值增加至它们的双亲节点。这样一来,所有的双亲节点都变成了新的叶节点,我们重复进行上述操作即可。当只剩一个节点(根节点)时,就可以得到最终的答案。
由于本题中的树是以数组形式给定的,因此只需要对数组进行一次逆序遍历,就等价于对整个树进行了一次从叶节点开始的,自底向上的遍历
class Solution {
public int minIncrements(int n, int[] cost) {
int ans = 0;
for (int i = n - 2; i > 0; i -= 2) {
ans += Math.abs(cost[i] - cost[i + 1]);
// 叶节点 i 和 i+1 的双亲节点下标为 i/2(整数除法)
cost[i / 2] += Math.max(cost[i], cost[i + 1]);
}
return ans;
}
}