题目链接

字符串变换

题目描述

已知有两个字串 $A,B$，及一组字串变换的规则（至多$6$个规则）:
$A_1\to B_1$
$A_2\to B_2$
…

规则的含义为：在$A$中的子串 $A_1$ 可以变换为$B_1$、$A_2$可以变换为$B_2$…。

例如：$A=$abcd，$B=$xyz

变换规则为：

abc → xu，ud → y，y → yz

则此时，$A$可以经过一系列的变换变为$B$
，其变换的过程为：

abcd → xud → xy → xyz

共进行了三次变换，使得$A$变换为$B$。

注意，一次变换只能变换一个子串，例如 $A＝$=aa，$B=$bb

变换规则为：

a → b

此时，不能将两个 a 在一步中全部转换为 b，而应当分两步完成。

输入格式

$AB$
$A_1{B}_1$
$A_2{B}_2$
… …

第一行是两个给定的字符串$A$和$B$。

接下来若干行，每行描述一组字串变换的规则。

所有字符串长度的上限为$20$。

输出格式

若在$10$ 步（包含$10$步）以内能将$A$变换为 $B$ ，则输出最少的变换步数；否则输出NO ANSWER!。

输入样例

abcd xyz
abc xu
ud y
y yz

输出样例

3

算法思想

根据题目描述，通过输入的规则将字串$A$变换为$B$，求最小步数，显然可以通过BFS求解。

朴素版广搜

分析数据范围，至多$6$个规则，在$10$ 步（包含$10$步）以内进行转换，如果直接进行BFS，在最坏情况下搜索的状态空间大约是 $6^{10}=60,466,176$，可以满足题目要求。

算法实现

• 将起始字符串$\text{A}$加入队列
• 只要队列不空，重复下面的处理：
  • 从队首取出一个字符串$\text{s}$
  • 如果变换到$\text{s}$的步数超过$10$，则无解，并结束搜索
  • 从$1\sim n$枚举变换规则$a_i\to b_i$
    • 只要字符串$\text{s}$中包含$a_i$
      • 将其替换为$b_i$，得到替换之后的字符串$\text{t}$
      • 如果替换后等于字符串$\text{B}$，则搜索结束，返回变换步数
      • 如果字符串$\text{t}$之前没有出现过，将其加入队列
      • 从下一个位置继续查找$a_i$

代码实现

#include <iostream>
#include <queue>
#include <unordered_map>
using namespace std;
const int N = 7;
string a[N], b[N];
string A, B;
int n;
int bfs()
{
    unordered_map<string, int> dis; //记录搜到到字符串的最小步数
    queue<string> q;
    dis[A] = 0;
    q.push(A);
    int ans = 0;
    while(q.size())
    {
        string s = q.front(); q.pop();
        if(dis[s] >= 10) { return -1; } //超过10步，返回-1
        for(int i = 0; i < n; i ++) //枚举变换规则
        {
            int idx = s.find(a[i]);
            while(idx != -1) //s中存在a[i]，可以变换
            {
                string t = s;
                t.replace(idx, a[i].size(), b[i]);
                if(t == B) return dis[s] + 1; //变换到B，返回变换步数
                if(!dis.count(t)) //第一次变换到t
                {
                    dis[t] = dis[s] + 1;
                    q.push(t);
                }
                idx = s.find(a[i], idx + 1); //从下一个位置继续查找a[i]进行替换
            }
        }
    }
    return -1;
}
int main()
{
    cin >> A >> B;
    while(cin >> a[n] >> b[n]) n ++;
    int ans = bfs();
    if(ans == -1) puts("NO ANSWER!");
    else cout << ans;
    return 0;
}

双向广搜

朴素版广搜虽然可以满足题目要求，但是要搜索的状态空间大约是 $6^{10}=60,466,176$，时间复杂度太高，可以使用双向广搜进行优化。

双向广搜，是指从起点和终点同时开始进行BFS，双向奔赴直到找到共同的目标为止。

使用双向广搜可以把搜索空间降到$2\times 6^5$，大大减少了要搜索的状态，剪枝效果明显。

使用双向广搜时要注意：

• 在双向广搜时，优先选择队列中状态数量较少的方向来扩展，可以优化搜索效率
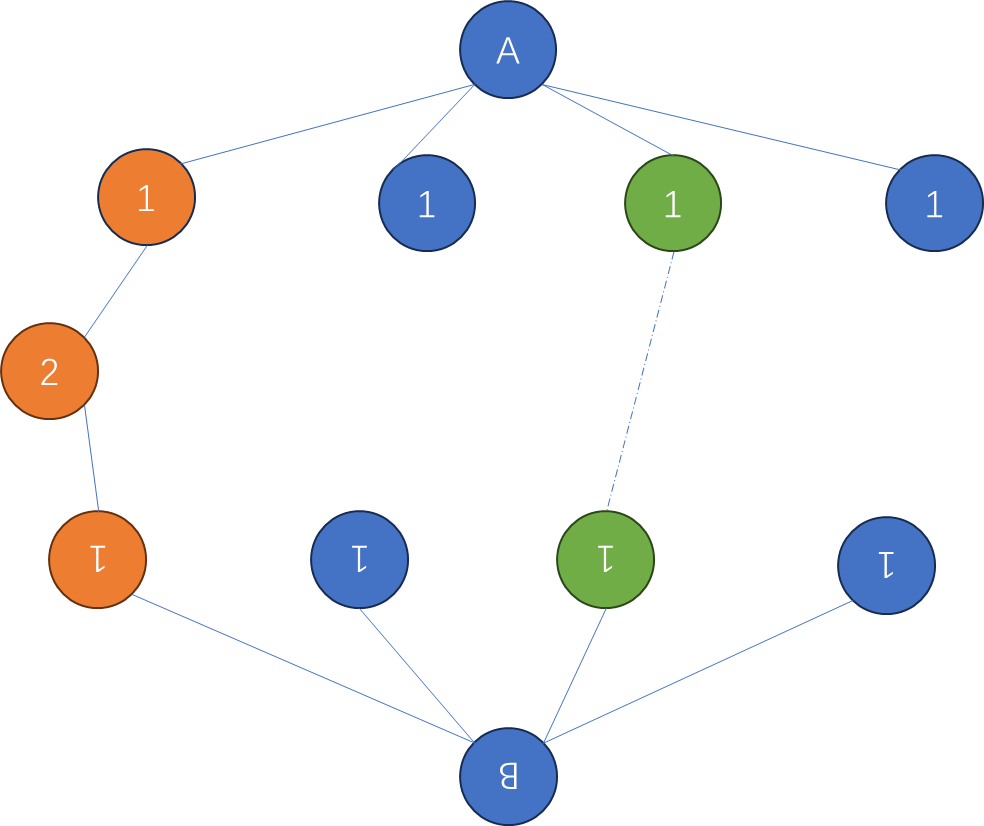
• 在扩展时，需要将一层的所有节点扩展完，不能只扩展一个点。如下图所示，第$2$层有$1,2,3,4$四个节点，则需要把这$4$个节点从队列中全部取出进行扩展。否则，找到的可能不是最少的转换次数。
  

代码实现

#include <iostream>
#include <queue>
#include <cstring>
#include <unordered_map>
using namespace std;
const int N = 6;
int n;
string A, B; //起点和终点
string a[N], b[N]; //变换规则
//从队列q中，将同层的节点全部扩展
int extend(queue<string>& q, unordered_map<string, int>& da, unordered_map<string, int>& db, 
    string a[N], string b[N])
{
    int d = da[q.front()]; //层数
    while(q.size() && da[q.front()] == d) //将同层的节点全部扩展
    {
        string s = q.front(); q.pop();
        for(int i = 0; i < n; i ++) //枚举在原字符串中使用替换规则
        {
            int idx = s.find(a[i]);
            while(idx != -1) //s中存在a[i]
            {
                string t = s;
                t.replace(idx, a[i].size(), b[i]);
                if(db.count(t)) return da[s] + db[t] + 1;//如果反方向已经搜索到该字符串t，则搜索结束，返回步数
                if(!da.count(t)) { da[t] = da[s] + 1; q.push(t);} //第一搜索到t
                idx = s.find(a[i], idx + 1); //从下一个位置继续查找a[i]进行替换
            }
        }
    }
    return 11;
}
int bfs()
{
    if(A == B) return 0;
    //双向搜索，扩展时分别进入不同队列
    queue<string> qa, qb;
    //da、db分别存储变换后的字符串到起点A和终点B的转换次数
    unordered_map<string, int> da, db;
    qa.push(A), qb.push(B); //起点和终点插入队列
    da[A] = db[B] = 0;
    int step = 0; //转换次数
    while(qa.size() && qb.size()) //两个队列都不为空
    {
        int t;
        if(qa.size() < qb.size()) //优先搜索状态数较少的方向
            t = extend(qa, da, db, a, b);
        else
            t = extend(qb, db, da, b, a);
        if(t <= 10) return t;
        if(++ step == 10) return -1; //变换10次没有结果
    }
    return -1;
}
int main()
{
    cin >> A >> B;
    while(cin >> a[n] >> b[n]) n ++;
    int t = bfs();
    if(t == -1) puts("NO ANSWER!");
    else cout << t << '\n';
    return 0;
}