1.牛的学术圈 I

思路

1.从大到小排序，把数组分成三段，[1, j] (j, j2] (j2, n]，j 以 i 为界限，j2 以 i - 1 为界限
2.第一部分引用数已经够了，第三部分引用数差太多，判断第一部分 + min(L, 第二部分)是否有 i 篇

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n, l;

int main(){
    scanf("%d%d", &n, &l);
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    sort(a + 1, a + n + 1, greater<int>());
    int res = 0;
    for(int i = 1, j = n, j2 = n; i <= n; i++){
        // 维护大于等于 i 和小于 i 的界限
        while(j && i > a[j]) j--;
        // 维护大于等于 i - 1 和小于 i - 1 的界限
        while(j2 && i - 1 > a[j2]) j2--;
        // 判断第一部分 + min(L, 第二部分)是否有 i 篇
        if(j + min(l, j2 - j) >= i){
            res = i;
        }
    }
    printf("%d", res);
    return 0;
}

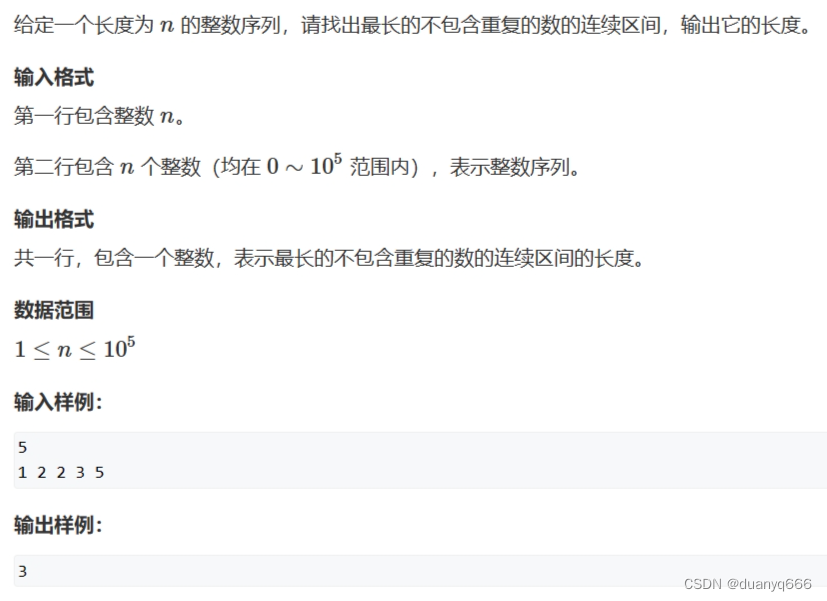
2.最长连续不重复子序列

思路

用 i 和 j 维护一组连续不重复子序列，用一个数组存储这个区间每个元素出现了多少次，如果出现次数大于 1，那就有重复元素，i 右移直到没有重复元素

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int n;

int main(){
    scanf("%d", &n);
    for(int i = 0; i < n; i++) scanf("%d", &a[i]);
    int res = 0;
    for(int i = 0, j = 0; j < n; j++){
        b[a[j]]++;
        while(b[a[j]] > 1){
            b[a[i]]--;
            i++;
        }
        res = max(res, j - i + 1);
    }
    printf("%d", res);
    return 0;
}

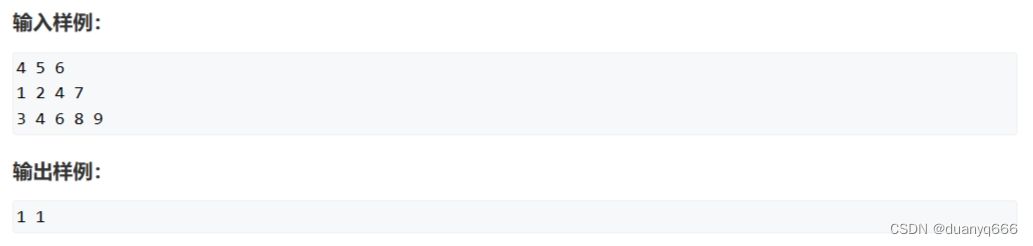
3.数组元素的目标和

思路

i 指针正序遍历 a 数组，j 指针倒序遍历 b 数组，如果和大了 j 左移，和小了 i 右移

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m, x;
int a[N], b[N];

int main(){
    scanf("%d%d%d", &n, &m, &x);
    for(int i = 0; i < n; i++) scanf("%d", &a[i]);
    for(int i = 0; i < m; i++) scanf("%d", &b[i]);
    int l = 0, r = m - 1;
    while(1){
        if(a[l] + b[r] == x){
            printf("%d %d", l, r);
            break;
        }
        while(a[l] + b[r] < x) l++;
        while(a[l] + b[r] > x) r--;
    }
    return 0;
}

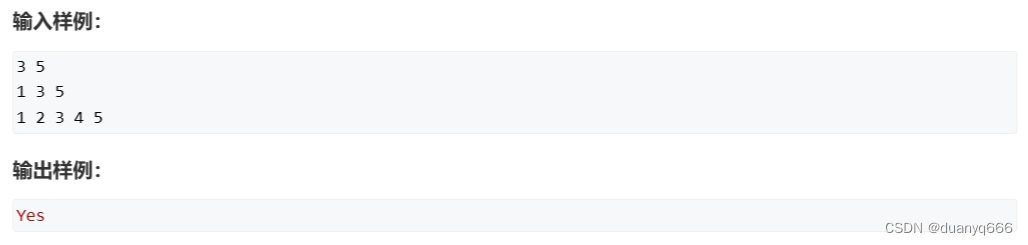
4.判断子序列

思路

i 指针枚举 a 数组，j 指针枚举 b 数组，j 指针一直右移，如果两个位置相等，i 指针右移

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int n, m;

int main(){
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i++) scanf("%d", &a[i]);
    for(int i = 0; i < m; i++) scanf("%d", &b[i]);
    int l = 0, r = 0;
    while(l < n && r < m){
        if(a[l] == b[r]) l++;
        r++;
    }
    printf("%s", (l == n ? "Yes" : "No"));
    return 0;
}

5.日志统计

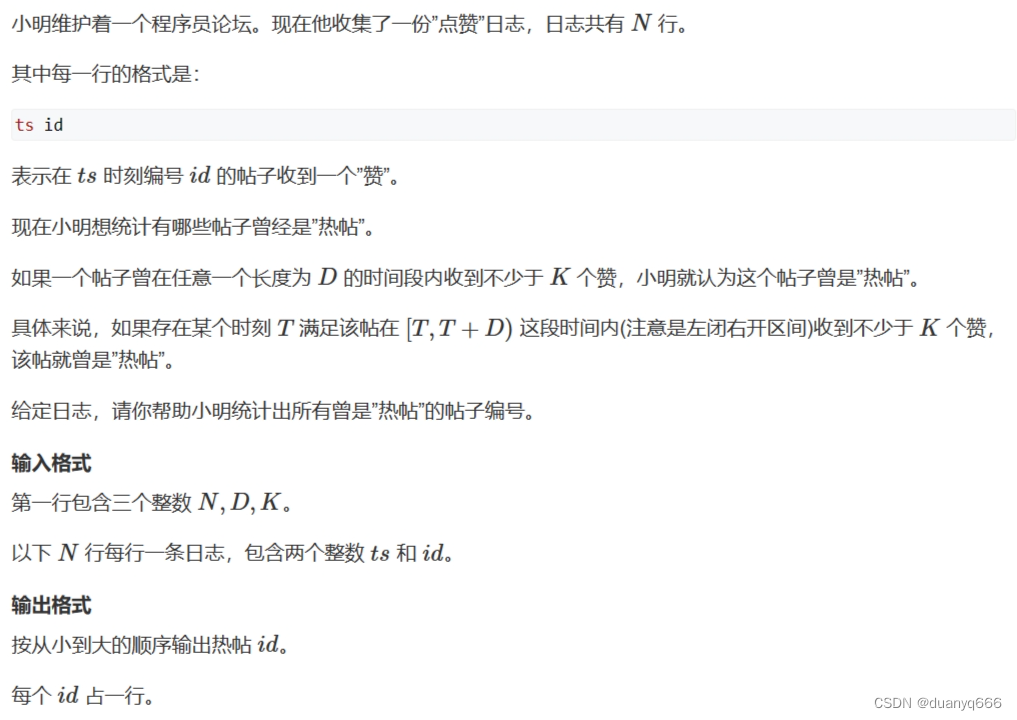
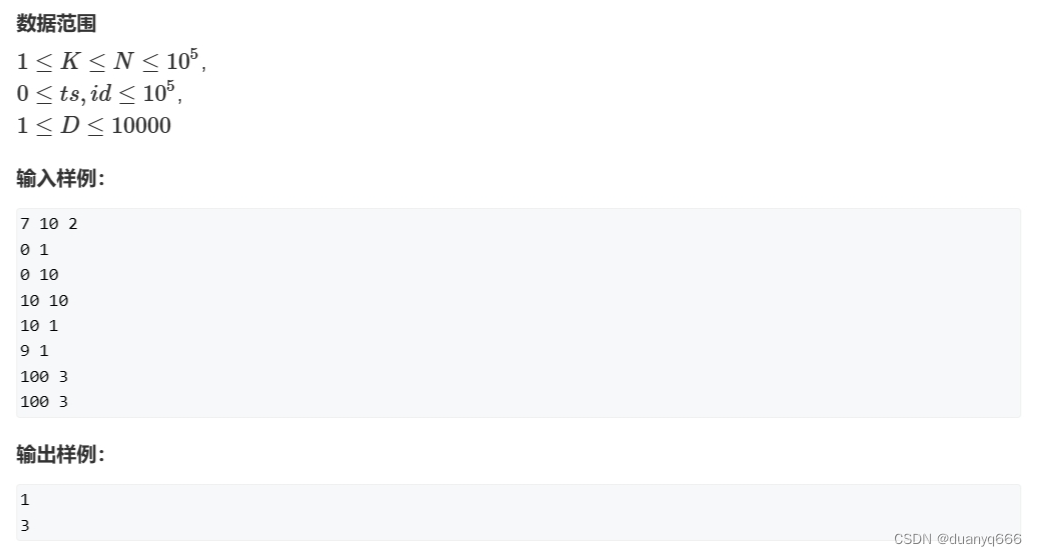
思路

根据时间排序，可以独立处理编号或者并行处理编号
1.独立处理编号：用 cnt 数组存储每个编号得到的赞，如果时间大于等于 d 了，那么左指针右移，如果当前右指针的编号赞大于等于 k 了，那就是热帖
2.并行处理编号：每次判断长为 k 的区间是否是一个编号，如果是一个编号且时间小于 d，那么就是热帖，然后再移动到下个编号区间

// 独立处理编号
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
pair<int, int> a[N];
int b[N], cnt[N];
int n, d, k;

int main(){
    scanf("%d%d%d", &n, &d, &k);
    int ts, id;
    for(int i = 0; i < n; i++){
        scanf("%d%d", &ts, &id);
        a[i] = make_pair(ts, id);
    }
    sort(a, a + n);
    for(int i = 0, j = 0; j < n; j++){
        int it = a[j].second;
        cnt[it]++;
        while(a[j].first - a[i].first >= d){
            cnt[a[i].second]--;
            i++;
        }
        if(cnt[it] >= k) b[it] = 1;
    }
    for(int i = 0; i <= 100000; i++){
        if(b[i]) printf("%d\n", i);
    }
    return 0;
}

// 并行处理编号
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
pair<int, int> a[N];
int b[N], cnt[N];
int n, d, k;

int main(){
    scanf("%d%d%d", &n, &d, &k);
    int ts, id;
    for(int i = 0; i < n; i++){
        scanf("%d%d", &ts, &id);
        a[i] = make_pair(id, ts);
    }
    sort(a, a + n);
    int l = 0, r = k - 1;
    while(r < n){
    	// 是一个编号区间
        if(a[l].first == a[r].first){
            if(a[r].second - a[l].second < d){
                printf("%d\n", a[l].first);
                // 移动到下一个编号区间
                while(r < n && a[l].first == a[r].first) r++;
                l = r, r += k - 1;
            }else{
                l++, r++;
            }
        }else{ // 不是一个编号区间
            while(r < n && a[l].first == a[r].first) r++;
            l = r, r += k - 1;
        }
    }
    return 0;
}

6.统计子矩阵

思路

1.计算前缀和
2.枚举上下边界，双指针枚举左右边界，如果矩阵和大了，左指针就右移
3.注意 l <= r

#include<iostream>
using namespace std;
const int N = 510;
int a[N][N];
int n, m, k;

int main(){
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            scanf("%d", &a[i][j]);
            a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
        }
    }
    // i, l   i, r
    // j, l   j, r
    long long cnt = 0;
    for(int i = 1; i <= n; i++){
        for(int j = i; j <= n; j++){
            for(int l = 1, r = 1; r <= m; r++){
                while(l <= r && a[j][r] - a[j][l - 1] - a[i - 1][r] + a[i - 1][l - 1] > k) l++;
                if(l <= r) cnt += r - l + 1;
            }
        }
    }
    printf("%lld", cnt);
    return 0;
}