现代谱估计是信号处理和统计领域的一个重要主题,它涉及从信号中估计其频谱内容的方法。频谱表示一个信号在不同频率上的成分强度。谱估计在许多应用中都很重要,如通信系统、雷达、音频处理、生物医学工程等领域。
目录
前言
一、基础知识
1、功率谱估计的方法
2、功率谱估计的应用
二、经典谱估计
1、BT法(间接法)
2、周期图法(直接法)
3、周期图法谱估计质量分析
4、经典谱估计方法改进
Bartlett平均周期图法
窗口处理法平均周期图
修正的周期图求平均法(Welch法)
三、AR模型谱估计
四、最大熵谱估计
总结
前言
以下是一些现代谱估计的常见方法:
-
傅里叶变换: 傅里叶变换是将信号从时域转换到频域的基本工具。它可以用来计算信号的频谱。
-
周期图法: 周期图法是通过计算信号的周期图(也称为功率谱密度)来估计信号的频谱。这是通过将信号分成小段,并计算每个段的傅里叶变换的平方来实现的。
-
自相关和互相关: 自相关函数和互相关函数提供了信号在时间域上的相关性信息。它们可以用于估计信号的频谱特性。
-
峰值搜索和拟合: 在频谱中寻找峰值并进行拟合是一种常见的谱估计方法。这通常用于精确估计信号的频率成分。
-
滤波方法: 采用各种滤波技术,如周期性平均、平滑滤波等,来估计信号的频谱特性。
-
高阶谱估计: 高阶谱估计方法包括二阶谱、三阶谱等。这些方法提供了关于信号非线性特性的更多信息。
-
波束形成技术: 在雷达和通信系统中,波束形成技术可以用于估计信号的方向性频谱。
-
时间-频域分析: 将信号在时间和频率上同时分析,例如采用短时傅里叶变换(STFT)或小波变换。
这些方法的选择取决于应用的具体要求、信号特性以及可用的计算资源。现代谱估计在处理非平稳信号、噪声干扰和实时应用方面具有挑战,因此研究人员一直在不断改进和提高这些方法。
一、基础知识
信号的功率谱和其自相关函数服从一对傅里叶变换关系。

1、功率谱估计的方法
2、功率谱估计的应用
在雷达信号处理中,回波功率谱的谱峰的密度、高度和位置可以确定运动目标的位置、辐射强
度和速度; 在被动式声呐信号处理中,谱峰的位置可以提供鱼雷的方向(方位角);在电子战中,信号的功率谱可以对敌方目标进行分类和识别。
二、经典谱估计
1、BT法(间接法)
BT法是先估计自相关函数, 然后进行傅里叶变换得到功率谱。

2、周期图法(直接法)

3、周期图法谱估计质量分析

4、经典谱估计方法改进
存在问题:BT法和周期图法估计功率谱都不是
一致估计,频率分辨率低。
解决方法:对周期图进行修正,使其满足一致估计条件。可以采用平滑处理的方法,使其方差减小。
- Bartlett平均周期图法
- 窗口处理法平均周期图
- Welch法(修正的周期图求平均法)
Bartlett平均周期图法
主要思想:对序列x(n)进行L次独立观测或将其分成L段,计算每组观测数据的周期图,再将L
个周期图加和后求平均。
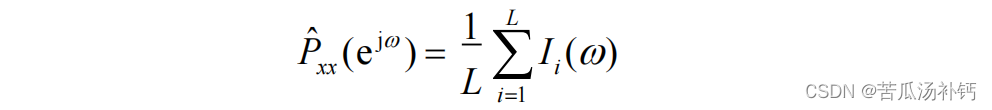
窗口处理法平均周期图
主要思想:用一适当的功率谱窗函数W(ejω)与周期图进行卷积,来达到使周期图平滑的目的。
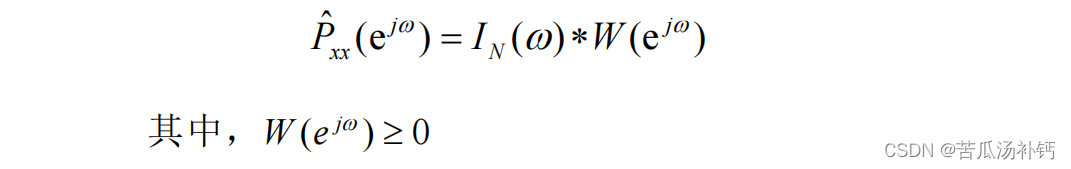
修正的周期图求平均法(Welch法)
主要思想:对Bartlett法进行修正,使之更适合FFT计算。
估计方法:
结论:传统的功率谱估计方法无论采取哪一种改进方法,总是以减少分辨率为代价,换取估计方差
的减少,提高分辨率的问题无法根本解决。
三、AR模型谱估计
自回归(AR)模型是一种用于时间序列建模的方法,其中每个观测值被认为是先前观测值的线性组合,加上白噪声。AR模型的频谱估计是通过分析自回归系数的幅度和相位来进行的。这里简要介绍AR模型的频谱估计:
-
AR模型表示: AR(p)模型中,当前时刻的观测值被表示为前p个时刻的线性组合,再加上白噪声。其数学表达式为:
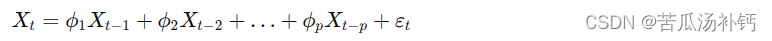
其中,Xt 是当前时刻的观测值,ϕ1,ϕ2,…,ϕp 是自回归系数,εt 是白噪声。
-
自相关函数(ACF): AR模型的自相关函数是描述观测值之间相关性的函数。自相关函数的性质与AR模型的自回归系数相关。在AR(p)模型中,自相关函数截尾在滞后p之后。
-
估计自回归系数: 通过拟合AR模型,可以估计自回归系数。这可以通过最小二乘法等方法完成。
-
频谱估计: AR模型的频谱估计可以通过自回归系数的幅度和相位信息来得到。频谱估计可以表示为:

-
绘制谱图: 可以绘制频谱图,显示不同频率上的能量分布。
注意,AR模型的阶数p需要事先确定。一般来说,可以通过分析ACF截尾的情况或使用信息准则(如AIC或BIC)来选择合适的阶数。
AR模型谱估计在时间序列分析和信号处理中得到广泛应用,能够提供有关信号频率分布的信息。
四、最大熵谱估计
最大熵谱估计(Maximum Entropy Spectral Estimation)是一种在信号处理和谱分析领域中用于估计信号频谱的方法。它基于最大熵原理,该原理认为在不知道其他信息的情况下,应该选择具有最大熵的模型作为估计。
最大熵谱估计的一般步骤:
-
收集数据: 首先,收集需要进行谱估计的信号数据。
-
选择约束条件: 约束条件是关于待估计谱的已知信息,如均值、方差等。这些条件有助于确定最合适的谱估计模型。
-
建立最大熵模型: 利用已知的约束条件建立最大熵模型,该模型描述了在满足这些条件的情况下谱的可能性分布。
-
优化过程: 通过最大化熵的方式,调整模型的参数以满足给定的约束条件。这通常涉及使用数学优化算法,如拉格朗日乘子法。
-
计算谱估计: 通过最优化的模型,计算信号的频谱估计。
最大熵谱估计的优势在于它充分考虑了已知的约束条件,同时尽量避免了对未知信息的主观假设。这使得它在面对有限数据和缺乏先验知识的情况下,能够提供相对可靠的频谱估计。




![DOM破坏BurpSuite学院(Up升级版[其实就是代码变多了])](https://img-blog.csdnimg.cn/direct/11d07b41b98e4ba4aafb26789a87cafa.png)


![[Angular 基础] - routing 路由(下)](https://img-blog.csdnimg.cn/direct/0713b655b7be46129338ece1505c100d.gif#pic_center)