数位dp 笔记

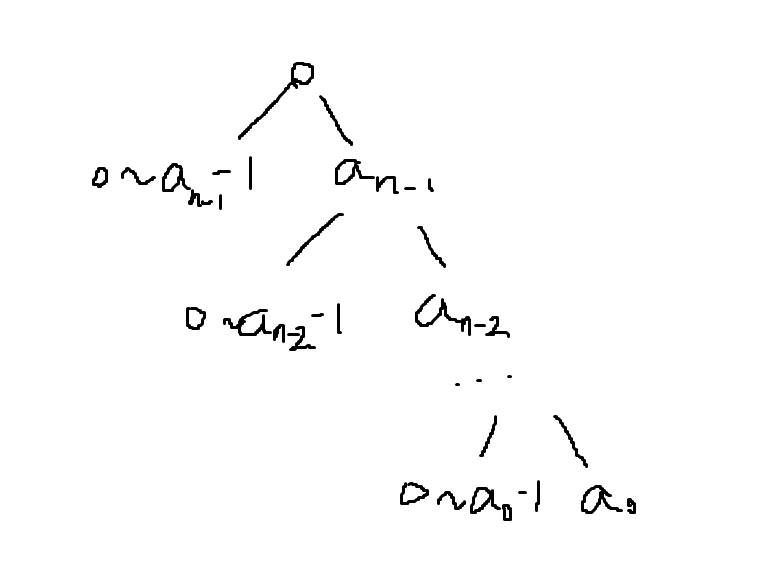
小技巧1:求区间[X, Y]可以转换为求F(Y) - F(X-1)

F(X)表示0~X中满足条件的数字个数

小技巧2：可以用树的形式来看

遍历最高位，每一位分为两种情况：未达到上界和达到上界

如果走到右边最底端需加1

度的数量

求给定区间 [X,Y]中满足下列条件的整数个数：这个数恰好等于 K 个互不相等的 B 的整数次幂之和。

例如，设 X=15,Y=20,K=2,B=2，则有且仅有下列三个数满足题意：

17=2^4+2^0
18=2^4+2^1
20=2^4+2^2

输入格式

第一行包含两个整数 X 和 Y，接下来两行包含整数 K 和 B。

输出格式

只包含一个整数，表示满足条件的数的个数。

数据范围

1≤X≤Y≤2^31−1,
1≤K≤20,
2≤B≤10

输入样例：

15 20
2
2

输出样例：

B进制上放K个1，在[X, Y]范围内的数量

左节点可放0或1

右节点只能放0或1，大于1时break

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;

const int N = 35;

int l, r, K, B;
int f[N][N];

void init()
{
	f[0][0] = 1;
	for(int i = 1; i < N; i ++)
	{
		for(int j = 0; j <= i; j ++)
		{
			if(!j)f[i][j] = 1;
			else f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
		}
	}
}

int C(int a, int b)
{
	if(a < b || b < 0)return 0;
	return f[a][b];
}

int dp(int n)
{
	if(!n)return 0;
	
	vector<int> nums;
	while(n)
	{
		nums.push_back(n % B);
		n /= B;
	}
	
	int res = 0, last = 0;
	for(int i = nums.size() - 1; i >= 0; i --)
	{
		int x = nums[i];
		
		if(x)//x>0才能走左分支 
		{
			res += C(i, K - last);
			if(x > 1)
			{
				res += C(i, K - last - 1);
				break;
			}
			else
			{
				last ++;
				if(last > K)break; //等于K时不能break，因为下一个还可以算左分支，或者如果一直放0也会走到右分支底端
			}
		}
		
		//只有走到底端(没有break出去)才能加1，不能放到循环外
		if(!i && last == K)res ++;//走到最后一步可能是1也可能是0 
	}
	return res;
}

int main()
{
	IOS
	init();
	cin >> l >> r >> K >> B;
	cout << dp(r) - dp(l - 1);
	
	return 0;
}

数字游戏

科协里最近很流行数字游戏。

某人命名了一种不降数，这种数字必须满足从左到右各位数字呈非下降关系，如 123，446。

现在大家决定玩一个游戏，指定一个整数闭区间 [a,b]，问这个区间内有多少个不降数。

注意：不降数不能包含前导零。

输入格式

输入包含多组测试数据。

每组数据占一行，包含两个整数 a 和 b。

输出格式

每行给出一组测试数据的答案，即 [a,b] 之间有多少不降数。

数据范围

1≤a≤b≤2^31−1

输入样例：

1 9
1 19

输出样例：

9
18

思路还是和模板差不多，关键点是找固定x时如何找不下降数的个数

可以用动态规划来找：

f[i][j]表示区间长度为i，第一个数字为j的不下降数个数

f[i][j] = $\sum_{k=j}^{9}$ f[i-1][k]

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;

const int N = 15;

int f[N][N];

void init()
{
	for(int i = 0; i <= 9; i ++)f[1][i] = 1;
	
	for(int i = 2; i < N; i ++)
	{
		for(int j = 0; j <= 9; j ++)
		{
			for(int k = j; k <= 9; k ++)
			{
				f[i][j] += f[i - 1][k];
			}
		}
	}
}

int dp(int n)
{
	if(!n)return 1;
	
	vector<int> nums;
	while(n)
	{
		nums.push_back(n % 10);
		n /= 10;
	}
	
	int res = 0, last = 0;
	for(int i = nums.size() - 1; i >= 0; i --)
	{
		int x = nums[i];
		
		for(int j = last; j < x; j ++)
		{
			res += f[i + 1][j];//关键点是这一步
		}
		
		if(x < last)break;
		last = x;
		if(!i)res ++;
	}
	return res;
} 

int main()
{
	IOS
	init();
	int l, r;
	while(cin >> l >> r)
	{
		cout << dp(r) - dp(l - 1) << endl;
	}
	
	return 0;
}

Windy数

Windy 定义了一种 Windy 数：不含前导零且相邻两个数字之差至少为 2 的正整数被称为 Windy 数。

Windy 想知道，在 A 和 B 之间，包括 A 和 B，总共有多少个 Windy 数？

输入格式

共一行，包含两个整数 A 和 B。

输出格式

输出一个整数，表示答案。

数据范围

1≤A≤B≤2×1e9

输入样例1：

1 10

输出样例1：

输入样例2：

25 50

输出样例2：

和上一题差不多

额外知识点为如何处理前导零，两点：

1.最高的那一位从1开始而不是从0开始

2.再枚举位数 1~总位数-1 加上f[i][1~9]

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;

const int N = 15;

ll f[N][10];

void init()
{
	for(int i = 0; i <= 9; i ++)f[1][i] = 1;
	
	for(int i = 2; i < N; i ++)
	{
		for(int j = 0; j <= 9; j ++)
		{
			for(int k = 0; k <= 9; k ++)
			{
				if(abs(j - k) >= 2)
				{
					f[i][j] += f[i - 1][k];
				}
			}
		}
	}
}

int dp(int n)
{
	if(!n)return 0;
	
	vector<int> nums;
	while(n)
	{
		nums.push_back(n % 10);
		n /= 10;
	}
	
	int res = 0, last = -9;
	for(int i = nums.size() - 1; i >= 0; i --)
	{
		int x = nums[i];
		for(int j = (i == nums.size() - 1); j < x; j ++)
		{
			if(abs(j - last) < 2)continue;
			res += f[i + 1][j];
		}
		if(abs(x - last) < 2)break;
		last = x;
		if(!i)res ++;
	}
	
	// 特殊处理有前导零的数
    //0也被当成前导零了，所以0是否算入需人为规定，如果算入则return 1 和res = 1，不算入就return 0和res = 0
	for(int i = nums.size() - 1; i >= 1; i --)
	{
		for(int j = 1; j <= 9; j ++)
		{
			res += f[i][j];
		}
	}
	return res;
}

int main()
{
	IOS
	init();
	int x, y;
	cin >> x >> y;
	cout << dp(y) - dp(x - 1); 
	
	return 0;
}

数字游戏 II

由于科协里最近真的很流行数字游戏。

某人又命名了一种取模数，这种数字必须满足各位数字之和 mod N 为 0。

现在大家又要玩游戏了，指定一个整数闭区间 [a.b]，问这个区间内有多少个取模数。

输入格式

输入包含多组测试数据，每组数据占一行。

每组数据包含三个整数 a,b,N。

输出格式

对于每个测试数据输出一行结果，表示区间内各位数字和 mod N 为 0 的数的个数。

数据范围

1≤a,b≤2^31−1,
1≤N<100

输入样例：

1 19 9

输出样例：

f[i][j][k]表示i位，首位为j，模数为k

其他一样，这题不处理前导零也没影响，但以防万一处理一下也没毛病（不处理时n=0时返回1）

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;

const int N = 15;

ll f[N][10][110];//i位 首位为j 模数为k 
int mod;

void init()
{
	for(int i = 0; i <= 9; i ++)f[1][i][i % mod] ++;
	
	for(int i = 2; i < N; i ++)
	{
		for(int j = 0; j <= 9; j ++)
		{
			for(int k = 0; k < mod; k ++)
			{
				for(int u = 0; u <= 9; u ++)
				{
					f[i][j][(j + k) % mod] += f[i - 1][u][k];
				}
			}
		}
	}
}

int dp(int n)
{
	if(!n)return 1;
	
	vector<int> nums;
	while(n)
	{
		nums.push_back(n % 10);
		n /= 10;
	}
	
	int res = 0, last = 0;
	for(int i = nums.size() - 1; i >= 0; i --)
	{
		int x = nums[i];
		for(int j = 0; j < x; j ++)
		{
			res += f[i + 1][j][(mod - last) % mod];
		}
		
		last = (last + x) % mod;
		if(!i && !last)res ++;
	}

	return res;
}

int main()
{
	IOS
	int x, y;
	while(cin >> x >> y >> mod)
	{
	    memset(f, 0, sizeof f);
	    init();
    	cout << dp(y) - dp(x - 1) << endl; 
	}
	
	
	return 0;
}

不要62

杭州人称那些傻乎乎粘嗒嗒的人为 62（音：laoer）。

杭州交通管理局经常会扩充一些的士车牌照，新近出来一个好消息，以后上牌照，不再含有不吉利的数字了，这样一来，就可以消除个别的士司机和乘客的心理障碍，更安全地服务大众。

不吉利的数字为所有含有 4 或 62 的号码。例如：62315,73418,88914 都属于不吉利号码。但是，61152 虽然含有 6 和 2，但不是连号，所以不属于不吉利数字之列。

你的任务是，对于每次给出的一个牌照号区间 [n,m]，推断出交管局今后又要实际上给多少辆新的士车上牌照了。

输入格式

输入包含多组测试数据，每组数据占一行。

每组数据包含一个整数对 n 和 m。

当输入一行为“0 0”时，表示输入结束。

输出格式

对于每个整数对，输出一个不含有不吉利数字的统计个数，该数值占一行位置。

数据范围

1≤n≤m≤1e9

输入样例：

1 100
0 0

输出样例：

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;

const int N = 15;

ll f[N][10];

void init()
{
	for(int i = 0; i <= 9; i ++)f[1][i] = 1;
	f[1][4] = 0;
	
	for(int i = 2; i < N; i ++)
	{
		for(int j = 0; j <= 9; j ++)
		{
			if(j == 4)continue;
			if(j == 6)
			{
				for(int k = 0; k <= 9; k ++)
				{
					if(k == 2 || k == 4)continue;
					f[i][j] += f[i - 1][k];
				}
				continue;
			}
			for(int k = 0; k <= 9; k ++)
			{
				if(k == 4)continue;
				f[i][j] += f[i - 1][k];
			}
		}
	}
}

int dp(int n)
{
	if(!n)return 1;
	
	vector<int> nums;
	while(n)
	{
		nums.push_back(n % 10);
		n /= 10;
	}
	
	int res = 0, last = 0;
	for(int i = nums.size() - 1; i >= 0; i --)
	{
		int x = nums[i];
		for(int j = 0; j < x; j ++)
		{
			if(j == 4 || last == 6 && j == 2)continue;
			res += f[i + 1][j];
		}
		
		if(last == 6 && x == 2)break;
		if(x == 4)break;
		last = x;
		if(!i)res ++;
	}

	return res;
}

int main()
{
	IOS
	init();
	int x, y;
	while(cin >> x >> y, x)
	{
		cout << dp(y) - dp(x - 1) << endl; 
	}
	
	return 0;
}

恨7不成妻

单身！

依然单身！

吉哥依然单身！

DS 级码农吉哥依然单身！

所以，他平生最恨情人节，不管是 214 还是 77，他都讨厌！

吉哥观察了 214 和 77 这两个数，发现：

2+1+4=7
7+7=7×2
77=7×11

最终，他发现原来这一切归根到底都是因为和 7 有关！

所以，他现在甚至讨厌一切和 7 有关的数！

什么样的数和 7 有关呢？

如果一个整数符合下面三个条件之一，那么我们就说这个整数和 7 有关：

整数中某一位是 7；
整数的每一位加起来的和是 7 的整数倍；
这个整数是 7 的整数倍。

现在问题来了：吉哥想知道在一定区间内和 7 无关的整数的平方和。

输入格式

第一行包含整数 T，表示共有 T 组测试数据。

每组数据占一行，包含两个整数 L 和 R。

输出格式

对于每组数据，请计算 [L,R] 中和 7 无关的数字的平方和，并将结果对 1e9+7 取模后输出。

数据范围

1≤T≤50,
1≤L≤R≤1e18

输入样例：

输出样例：

236
221
0

f[i][j][a][b]表示i位数字，首位为j，模数为a，各个数字之和的模数为b

存三个值：个数、a1+a2+...、 $a1^{2}+a2^{2}+...$

$(ja1)^{2} = (j*10^i +a1)^2 =j*j*10^i*10^i+2*j*10^i+a1*a1$

所以 $(ja_1)^2+(ja_2)^2+...=(j*10^i)*t + 2*j*10^i+(a_1+a_2+...)+a_1^2+a_2^2+...$

推出这个公式后就能做了

取模很容易出错，建议先写完原式后再添加取模，多注意些

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;

const int N = 20, P = 1e9 + 7;

struct F
{
	ll s0, s1, s2;
}f[N][10][7][7];
ll shi7[N], shi9[N];

int mod(ll x, int y)
{
	return (x % y + y) % y;
}

void init()
{
	for(int i = 0; i <= 9; i ++)
	{
		if(i == 7)continue;
		auto &v = f[1][i][i % 7][i % 7];
		v.s0 = 1;
		v.s1 = i;
		v.s2 = i * i; 
	}
	
	ll res = 10;
	for(int i = 2; i < N; i ++, res *= 10)
	{
		for(int j = 0; j <= 9; j ++)
		{
			if(j == 7)continue;
			
			for(int a = 0; a <= 6; a ++)
			{
				for(int b = 0; b <= 6; b ++)
				{
					for(int k = 0; k <= 9; k ++)
					{
						if(k == 7)continue;
						auto &v = f[i][j][a][b];
						auto &v1 = f[i - 1][k][mod(a - j * res % 7, 7)][mod(b - j, 7)];
						v.s0 = (v.s0 + v1.s0) % P;
						v.s1 = (v.s1 + j * (res % P) % P * v1.s0 % P + v1.s1) % P;
						v.s2 += j * j % P * (res % P) % P * (res % P) % P * v1.s0 % P + 2ll * j * (res % P) % P * v1.s1 % P + v1.s2;
						v.s2 %= P;
					}
				}
			}
		}
	}
	
	shi7[0] = shi9[0] = 1;
	for(int i = 1; i < N; i ++)
	{
		shi7[i] = (shi7[i - 1] * 10) % 7;
		shi9[i] = (shi9[i - 1] * 10) % P;
	}
}

F get(int i, int j, int a, int b)
{
	ll s0 = 0, s1 = 0, s2 = 0;
	for(int u1 = 0; u1 < 7; u1 ++)
	{
		if(u1 == a)continue;
		for(int u2 = 0; u2 < 7; u2 ++)
		{
			if(u2 == b)continue;
			auto &v = f[i][j][u1][u2];
			s0 = (s0 + v.s0) % P;
			s1 = (s1 + v.s1) % P;
			s2 = (s2 + v.s2) % P;
		}
	}
	return {s0, s1, s2};
}

int dp(ll n)
{
	if(!n)return 0;
	
	ll ttt = n % P;	
	vector<int> nums;
	while(n)
	{
		nums.push_back(n % 10);
		n /= 10;
	}
	
	ll res = 0, last_a = 0, last_b = 0;
	for(int i = nums.size() - 1; i >= 0; i --)
	{
		int x = nums[i];
		for(int j = 0; j < x; j ++)
		{
			if(j == 7)continue;
			
			int a = mod(-last_a * shi7[i + 1], 7), b = mod(-last_b, 7);
			auto v = get(i + 1, j, a, b);
			
			res = mod(res + (last_a % P) * (last_a % P) % P * shi9[i + 1] % P * shi9[i + 1] % P * v.s0 % P
			 + 2ll * (last_a % P) * shi9[i + 1] % P * v.s1 % P + v.s2, P);
		}
		
		if(x == 7)break;
		last_a = last_a * 10 + x;
		last_b += x;
		if(!i && last_a % 7 && last_b % 7)res = mod(res + ttt * ttt, P); 
	}
	
	return res % P;
}

int main()
{
	IOS
	init();
	int _;
	cin >> _;
	while(_ --)
	{
		ll l, r;
		cin >> l >> r;
		cout << mod(dp(r) - dp(l - 1), P) << endl;
	}
	
	return 0;
}