LeetCode：1976. 到达目的地的方案数（spfa + 记忆化 Java）

news2024/11/15 7:01:42

1976. 到达目的地的方案数

原题链接

题目描述：

实现代码与解析：

spfa + 记忆化

原理思路：

1976. 到达目的地的方案数

原题链接

1976. 到达目的地的方案数

题目描述：

你在一个城市里，城市由 n 个路口组成，路口编号为 0 到 n - 1 ，某些路口之间有双向道路。输入保证你可以从任意路口出发到达其他任意路口，且任意两个路口之间最多有一条路。

给你一个整数 n 和二维整数数组 roads ，其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。

请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大，将结果对 109 + 7 取余后返回。

示例 1：

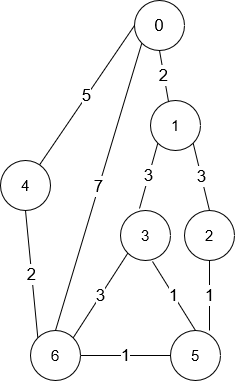
输入：n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
输出：4
解释：从路口 0 出发到路口 6 花费的最少时间是 7 分钟。
四条花费 7 分钟的路径分别为：
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

示例 2：

输入：n = 2, roads = [[1,0,10]]
输出：1
解释：只有一条从路口 0 到路口 1 的路，花费 10 分钟。

提示：

1 <= n <= 200
n - 1 <= roads.length <= n * (n - 1) / 2
roads[i].length == 3
0 <= ui, vi <= n - 1
1 <= timei <= 109
ui != vi
任意两个路口之间至多有一条路。
从任意路口出发，你能够到达其他任意路口。

实现代码与解析：

spfa + 记忆化

public class Solution {
    public static final int N = (int) 210;
    public static final int M = N * N;
    public static final long MOD = (long) 1e9 + 7;
    int[] w = new int[M], h = new int[N], e = new int[M], ne = new int[M];  // 邻接表
    long[] dist = new long[N];
    int idx;
    boolean[] st = new boolean[N]; // 判断是否走过
    long[] mer = new long[N]; // 记忆化数组
    // 加边方法
    public void add(int a, int b, int c) {
        e[idx] = b; w[idx] = c; ne[idx] = h[a]; h[a] = idx++;
    }

    public int countPaths(int n, int[][] roads) {

        // 初始化表头
        Arrays.fill(h, -1);

        // 加边，赋权重
        for (int i = 0; i < roads.length; i++) {
            int a = roads[i][0];
            int b = roads[i][1];
            int c = roads[i][2];
            add(a, b, c);
            add(b, a, c);
        }

        // spfa获取最短路
        long min = spfa(n);
        Arrays.fill(mer, -1);
        Arrays.fill(st, false);
        // 反向dfs获取最短路的个数
        // 利用记忆化搜索优化
        long res = dfs(n - 1, min);
        res %= MOD;
        System.out.println(res);
        return (int)res;
    }

    // spfa 算法模板，原理是利用减小的路径长度对应的节点去更新其他的，图论万能的算法，而且也是最好记的
    public long spfa(int n) {

        Arrays.fill(dist, Long.MAX_VALUE);
        Queue<Integer> q = new LinkedList<>();
        q.offer(0);
        dist[0] = 0;
        st[0] = true;

        while (!q.isEmpty()) {
            int t = q.peek();
            q.poll();
            st[t] = false;
            for (int i = h[t]; i != -1; i = ne[i]) {
                int j = e[i];
                if (dist[j] > dist[t] + w[i]) {
                    dist[j] = dist[t] + w[i];
                    if (!st[j]) {
                        q.offer(j);
                        st[j] = true;
                    }
                }
            }
        }
        return dist[n - 1];
    }

    public long dfs(int cur, long d) {

        if (dist[cur] != d) return 0;
        if (cur == 0) return 1;
        if (mer[cur] != -1) return mer[cur]; // 如果已经记录过，不再走，直接获取此结果即可
        long res = 0;
        for (int i = h[cur]; i != -1; i = ne[i]) {
            int j = e[i];
            if (st[j]) continue;
            res += dfs(j, d - w[i]);
            res %= MOD;
        }
        mer[cur] = res;
        return res;
    }
}