目录
1.增加虚点建图:
2.抽象图的迪杰斯特拉:
3.用bitset优化弗洛伊德:
4.有向图的Prim/kruskal:
1.增加虚点建图:

我们当然可以每一层与上一层的点再连上一条边,但这样子边太多了超内存,我们可以对于每一层建立两个虚的中站,其中一个每一层的点到中站的距离=0,他连一条边与上面的站,权值为两层的距离,另一个向下(注意边都是单向边,否则会产生新的路径)。
2.抽象图的迪杰斯特拉:
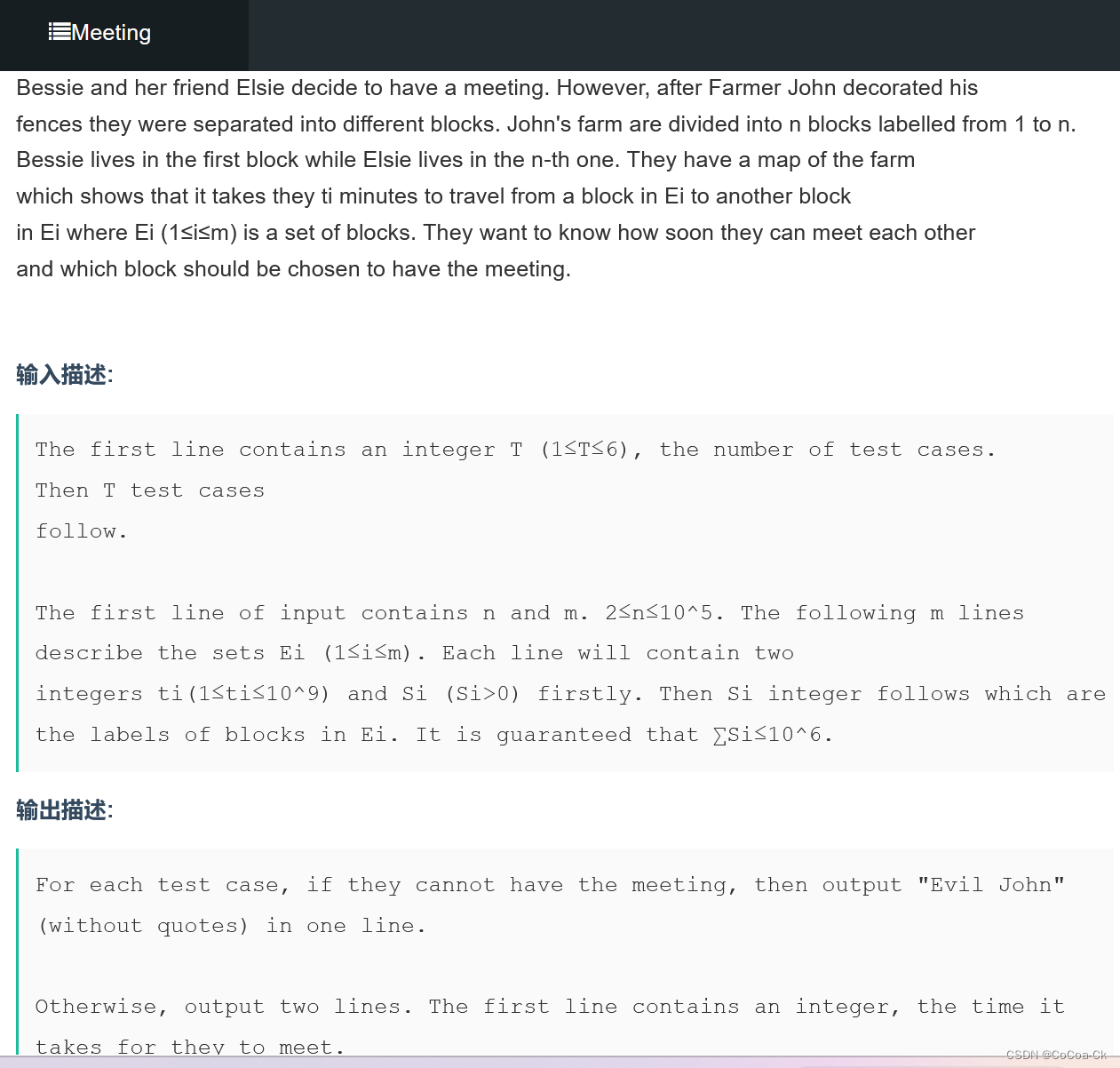
每一个集合里如果互相连边的话边太多了,我们不妨把一个集合当成一个抽象的点,然后去跑迪杰斯特拉。因此我们只要记录每一个点属于的集合以及每一个集合中含有的点即可。
我们还是在枚举点,只不过我们要再多一个for来表示取出的集合,同时我们保证集合只被枚举一次,因为重复的集合不会使结果更优。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int t,n,m,t1[100010],ti,si,k;
vector<int> es[1000005];
vector<int> inque[100005];
int dis[2][100010];
bool vistuan[100010],visdian[100010];
int ans[100010];
struct node{
int zhi,dian;
bool operator<(const node &a) const{
return zhi>a.zhi;
}
};
priority_queue<node> q;
void dij(int s,int f){
memset(vistuan,0,sizeof(vistuan));
memset(visdian,0,sizeof(visdian));
dis[f][s]=0;
q.push({0,s});
while(!q.empty()){
node ck=q.top();
q.pop();
if(visdian[ck.dian]==1) continue;
visdian[ck.dian]=1;
for(int i=0;i<inque[ck.dian].size();i++){
int j=inque[ck.dian][i];
if(vistuan[j]==1) continue;
vistuan[j]=1;
for(int k=0;k<es[j].size();k++){
int w=es[j][k];
if(visdian[w]==1) continue;
if(dis[f][w]>ck.zhi+t1[j]){
dis[f][w]=ck.zhi+t1[j];
q.push({dis[f][w],w});
}
}
}
}
}
signed main(){
cin>>t;
int i1=1;
while(t--){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++) inque[i].clear();
memset(dis,0x7f7f7f7f,sizeof(dis));
for(int i=1;i<=m;i++){
es[i].clear();
scanf("%lld%lld",&ti,&si);
t1[i]=ti;
for(int j=1;j<=si;j++){
scanf("%lld",&k);
es[i].push_back(k);
inque[k].push_back(i);
}
}
dij(1,0);
dij(n,1);
long long ans_tmp=1e18;
int ans_len=0;
for(int i=1;i<=n;i++)
{
if(max(dis[0][i],dis[1][i])<ans_tmp)
{
ans_tmp=max(dis[0][i],dis[1][i]);
ans_len=0;
ans[ans_len++]=i;
}
else if(max(dis[0][i],dis[1][i])==ans_tmp)
{
ans[ans_len++]=i;
}
}
printf("Case #%d: ",i1++);
if(ans_len==0||ans_tmp==1e18)
{
printf("Evil John\n");
}
else
{
printf("%lld\n",ans_tmp);
for(int i=0;i<ans_len;i++)
{
printf("%lld",ans[i]);
if(i==ans_len-1)
printf("\n");
else
printf(" ");
}
}
}
}3.用bitset优化弗洛伊德:

我们把>号表示成一条有向边即可。这样子我们就是求任意两点是否可以到,我们很容易想到弗洛伊德算法,但是这个复杂度铁超,我们发现,弗洛伊德还算出了最短距离,而我们只需要0/1,因此我们想到bitset优化,我们把每一个点能否到其他点记作01串,这样子当我们枚举中转使,只要或上中转的01串即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
struct node{
int dian,next;
}edge[100010];
bitset<1005> dp[1010];
int n,m,head[1010],cnt,x,y;
void merge(int x,int y){
edge[++cnt].dian=y;
edge[cnt].next=head[x];
head[x]=cnt;
}
int main(){
cin>>n>>m;
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
merge(x,y);
dp[x][y]=1;
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
if(i==k) continue;
if(dp[i][k]==0) continue;
dp[i]|=dp[k];
}
}
int ans=0;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
if(dp[i][j]==1||dp[j][i]==1) continue;
ans++;
}
}
cout<<ans;
}4.有向图的Prim/kruskal:
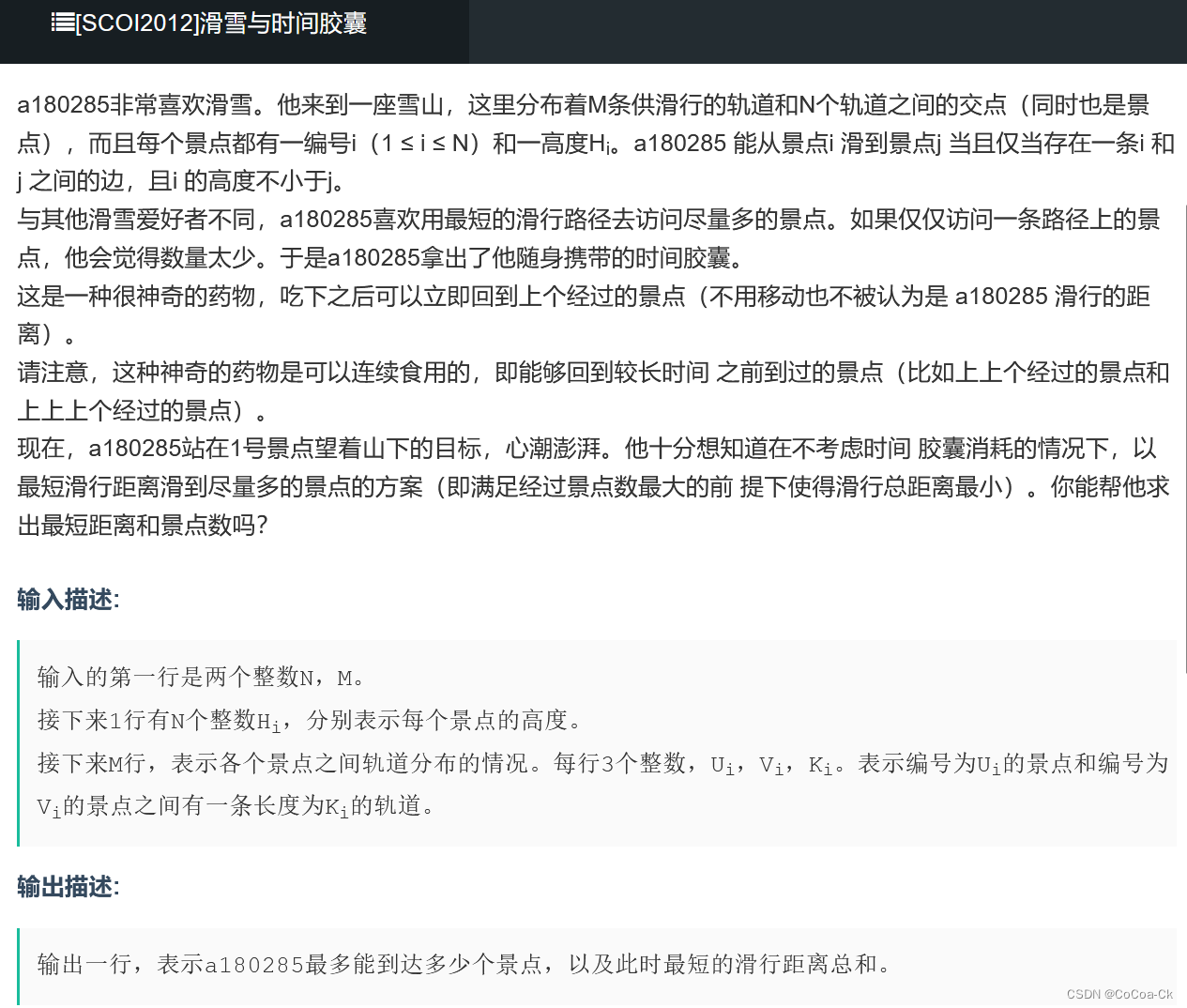
显然,我们先建个由高度决定的有向边,我们再跑一个DFS,记录哪个点可否到达,这样子,我们就可以得到类似于树的结构,假如他是无向边,我们就是求个最小生成树,但是因为是有向边,我们不可以直接跑这两个算法,我们不妨想想是为什么?
其实,问题就在于你无法保证那条连的边是可以按照正确方向走的,或者说,按照他走可能走不通,而这是由高度造成的,于是我们可以按照高度,从上到下建立关系,我们不妨先看1,2层,当他们建好时再考虑第3层,依次类推即可。
如果用Prim算法,我们只需先按照高度排序即可。
如果用kruskal算法,我们在存边时在记录下两者中较低的高度sort即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,h[100010],vis[100010],u,v,k,cnt,fa[100010];
struct node{
int x,y,z,h;
}bian[1000100];
vector<int> edge[1000100];
void dfs(int ck){
cnt++;
vis[ck]=1;
for(int i=0;i<edge[ck].size();i++){
int yy=edge[ck][i];
if(vis[yy]==1) continue;
dfs(yy);
}
return;
}
bool cmp(node a,node b){
if(a.h==b.h) return a.z<b.z;
return a.h>b.h;
}
int find(int x){
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&h[i]);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&k);
if(h[u]>h[v]) edge[u].push_back(v);
else if(h[u]<h[v]) edge[v].push_back(u);
else{
edge[u].push_back(v);
edge[v].push_back(u);
}
bian[i].x=u;
bian[i].y=v;
bian[i].z=k;
bian[i].h=min(h[u],h[v]);
}
dfs(1);
cout<<cnt<<" ";
long long ans=0;
for(int i=1;i<=n;i++) fa[i]=i;
sort(bian+1,bian+m+1,cmp);
for(int i=1;i<=m;i++){
int xx=bian[i].x;
int yy=bian[i].y;
if(vis[xx]==0||vis[yy]==0) continue;
int xxx=find(xx);
int yyy=find(yy);
if(xxx==yyy) continue;
ans+=bian[i].z;
fa[xxx]=yyy;
}
cout<<ans;
}