高级大数据技术实验一 scala编程

news2024/9/24 13:26:13

高级大数据技术实验一 scala编程

写的不是很好，大家多见谅！

1. 计算水仙花数

实验目标;

（1）掌握scala的数组，列表，映射的定义与使用

（2）掌握scala的基本编程

实验说明

水仙花数是指其个位、十位、百位三个数的立方和等于这个数本身，用Scala编程求出所有水仙花数。

概况描述水仙花数（Narcissistic number）也被称为超完全数字不变数（pluperfect digital invariant, PPDI）、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数（Armstrong number），水仙花数是指一个 3 位数，它的每个位上的数字的 3次幂之和等于它本身。例如：1^3 + 5^3+ 3^3 = 153。

定义水仙花数只是自幂数的一种，严格来说3位数的3次幂数才称为水仙花数。

问题分析根据“水仙花数”的定义，判断一个数是否为“水仙花数”，最重要的是要把给出的三位数的个位、十位、百位分别拆分，并求其立方和（设为s），若s与给出的三位数相等，三位数为“水仙花数”，反之，则不是。

附：其他位数的自幂数名字一位自幂数：独身数三位自幂数：水仙花数四位自幂数：四叶玫瑰数五位自幂数：五角星数六位自幂数：六合数七位自幂数：北斗七星数八位自幂数：八仙数九位自幂数：九九重阳数十位自幂数：十全十美数

代码实现水仙花数是指其个位、十位、百位3个数的立方和等于这个数本身，请用Scala编程求出100～999之间的所有水仙花数。

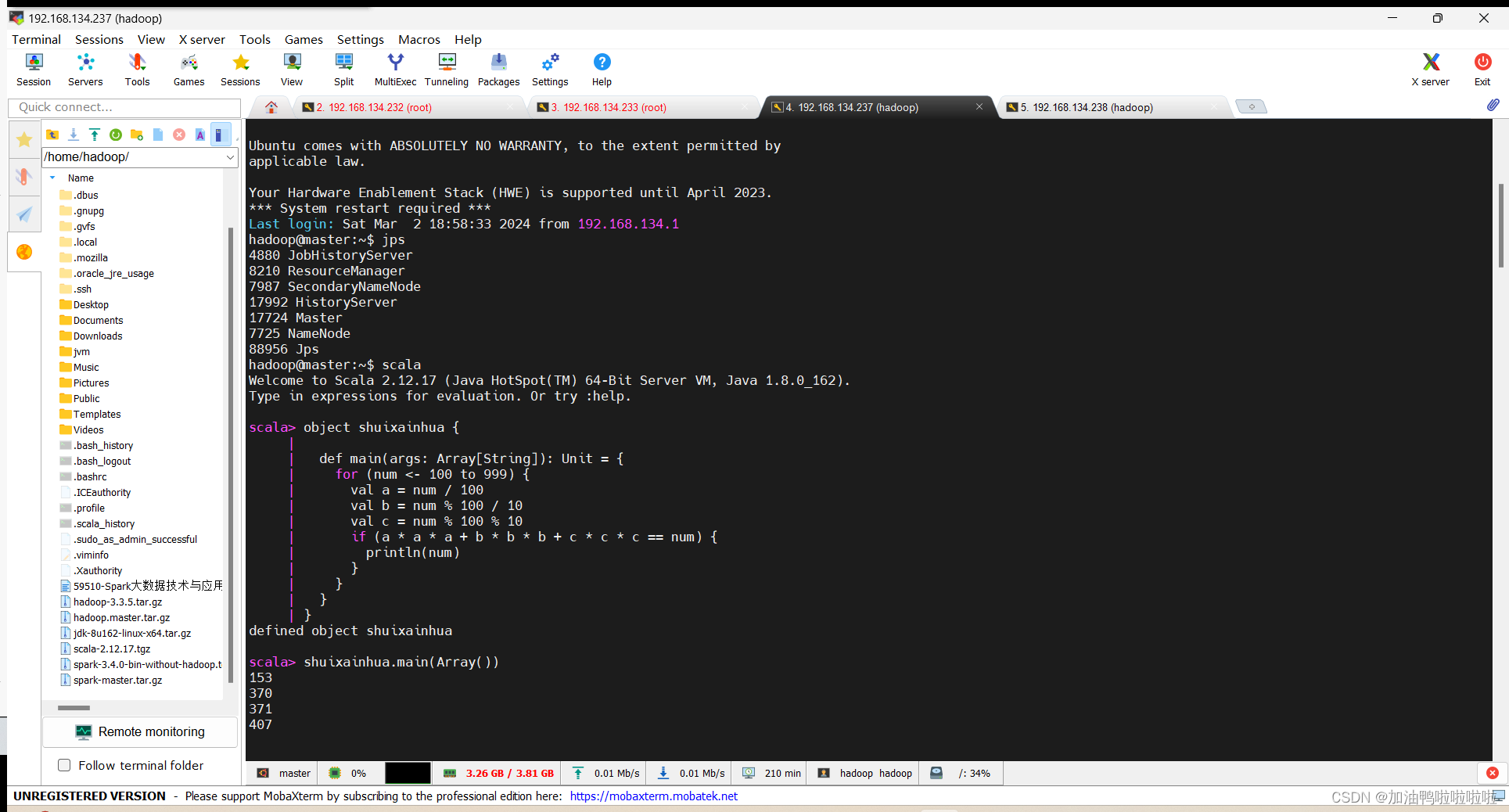
object shuixainhua {

  def main(args: Array[String]): Unit = {
    for (num <- 100 to 999) {
      val a = num / 100
      val b = num % 100 / 10
      val c = num % 100 % 10
      if (a * a * a + b * b * b + c * c * c == num) {
        println(num)
      }
    }
  }
}
shuixainhua.main(Array())

在这里插入图片描述

使用scala编写函数过滤文本中的回文单词
实验目标;

（3）掌握scala的数组，列表，映射的定义与使用

（4）掌握scala的for循环与if判断的使用

（5）掌握scala的函数式编程

实验说明：

回文是指正向和逆向读起来相同的词，英语中也存在着回文现象，如“mom”和“dad”。

参照给出的英文文档word.txt,使用scala编程读取文件，并且编写一个函数判断文档中的每个单词是否为回文单词，若是则输出该单词。

实现思路及步骤：

（1）读取word.txt数据，将数据

（2）使用flatMap()方法获取缓存区里面的数据，并使用空格进行分割。

（3）定义函数isPalindrom(word:String)

(4) 在函数中判断单词正向与逆向是否一样，若是则输出该单词

（5）调用isPalindrom 函数

第一种：
import scala.io.Source
def isPalindrome(word: String): Boolean = {
  word.reverse == word
}
val lines = Source.fromFile("word.txt").getLines
val words = lines.flatMap(line => line.split(" "))
words.filter(word => isPalindrome(word)).foreach(println)

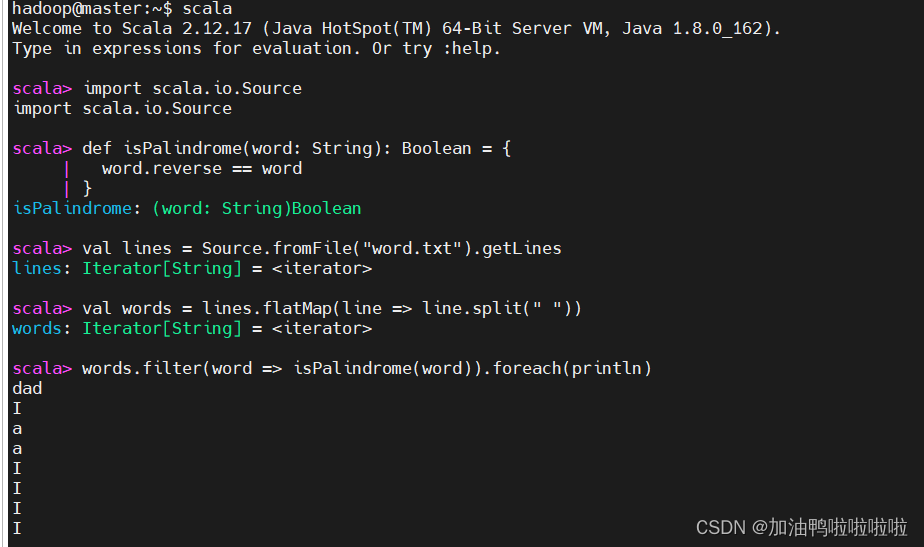
在这里插入图片描述

第二种：
import scala.io.Source
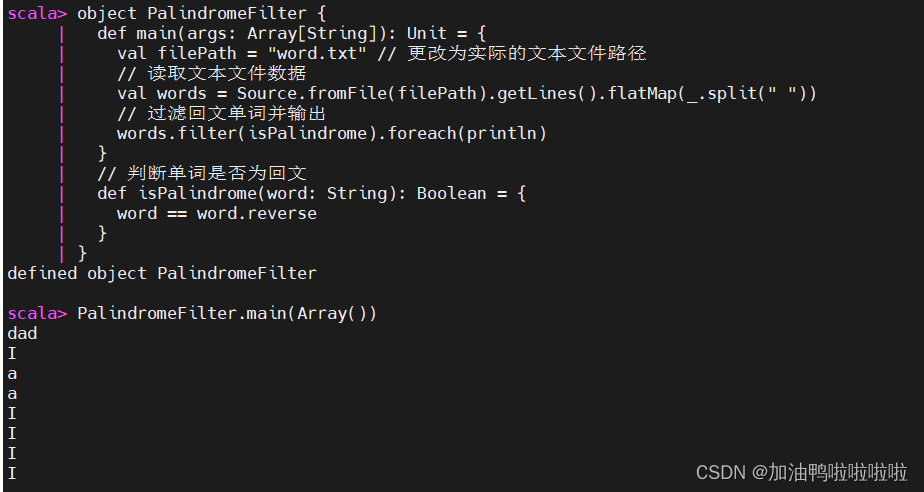
object PalindromeFilter {
  def main(args: Array[String]): Unit = {
    val filePath = "word.txt" // 更改为实际的文本文件路径
    // 读取文本文件数据
    val words = Source.fromFile(filePath).getLines().flatMap(_.split(" "))
    // 过滤回文单词并输出
    words.filter(isPalindrome).foreach(println)
  }
  // 判断单词是否为回文
  def isPalindrome(word: String): Boolean = {
    word == word.reverse
  }
}
PalindromeFilter.main(Array())

在这里插入图片描述

使用scala编程输出九九乘法表：
实验目标：

（1）掌握scala循环的使用

（2）掌握scala函数式编程

实验说明：

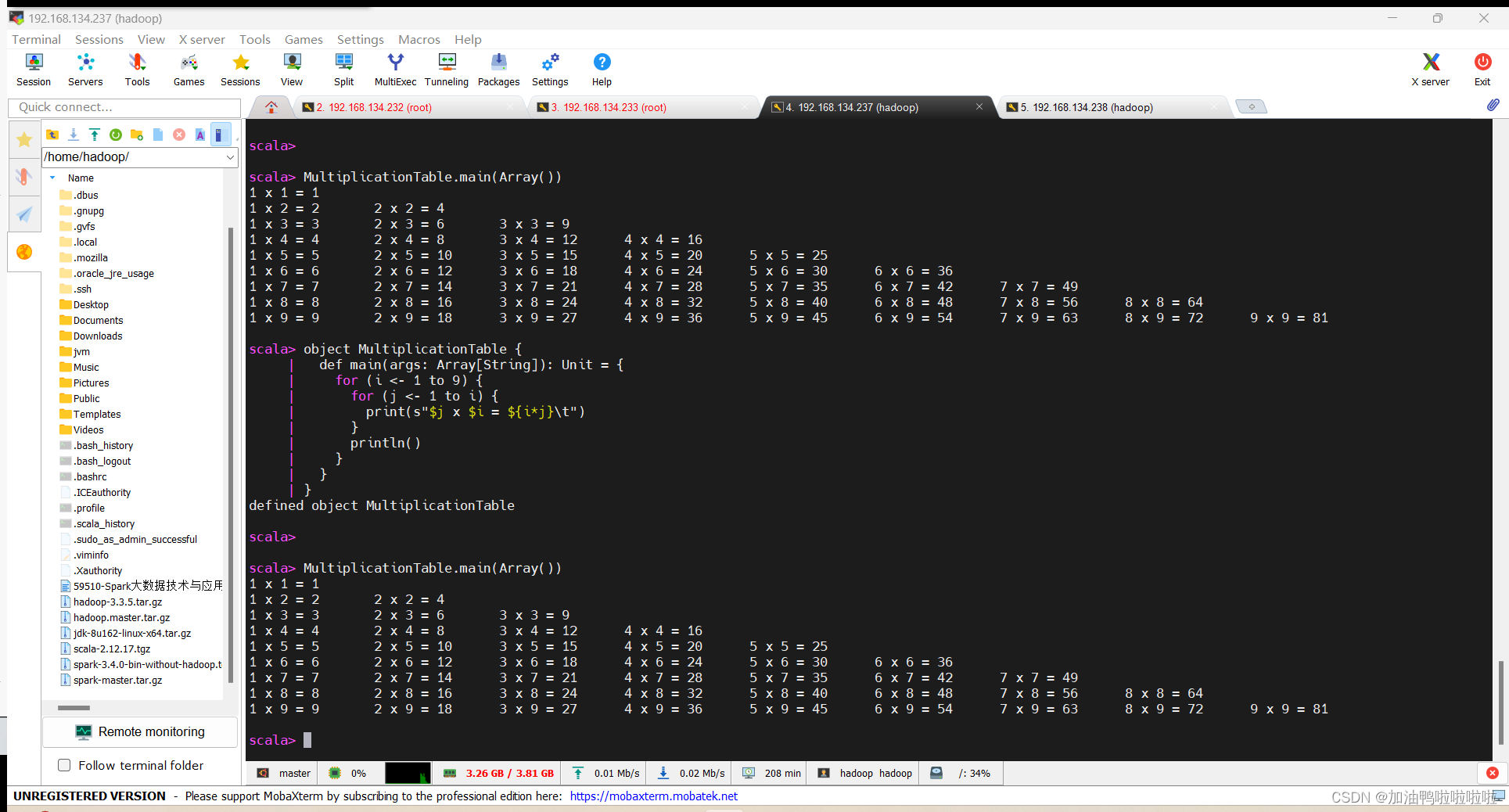
九九乘法表是我国古代人民的智慧结晶，在春秋战国时代就已经在筹算中运算，到明代则改良病用在算盘上。现需要使用scala编程输出九九乘法表，要求输出效果如图所示：

\3. 使用scala编程输出九九乘法表：

实验目标：

（1）掌握scala循环的使用

（2）掌握scala函数式编程

实验说明：

九九乘法表是我国古代人民的智慧结晶，在春秋战国时代就已经在筹算中运算，到明代则改良病用在算盘上。现需要使用scala编程输出九九乘法表。

object MultiplicationTable {
  def main(args: Array[String]): Unit = {
    for (i <- 1 to 9) {
      for (j <- 1 to i) {
        print(s"$j x $i = ${i*j}\t")
      }
      println()
    }
  }
}
MultiplicationTable.main(Array())