- 博主简介:努力学习和进步中的的22级计科生
- 博主主页: @Yaoyao2024
- 每日一句: “ 路虽远,行则将至。事虽难,做则可成。”
前言
前言:动规五部曲
以下是《代码随想录》作者总结的动规五部曲
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式(状态转移方程)
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
所有动态规划问题中,一个状态一定由上一个状态推导而来,这点就有别于贪心,贪心没有状态的推导更别说什么公式,贪心只是从局部选取最优解。
例如:有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
动态规划中dp[j]是由dp[j-weight[i]]推导出来的,然后取max(dp[j], dp[j - weight[i]] + value[i])。
但如果是贪心呢,每次拿物品选一个最大的或者最小的就完事了,和上一个状态没有关系。
所以贪心解决不了动态规划的问题。
62. 不同路径
题目链接

🌷思路:
这题首先思想肯定还是图论里的深搜,将机器人的路径看作一个二叉树,求为终点的叶子节点的数量:

class Solution {
private:
int dfs(int x, int y, int m, int n){
if(x>m||y>n) return 0;//当前位置已经越界
if(x == m && y == n) return 1;
return dfs(x+1,y,m,n)+dfs(x,y+1,m,n);
}
public:
int uniquePaths(int m, int n) {
return dfs(1,1,m,n);
}
};
但是发现,这种深搜的解题思路会超出时间限制:
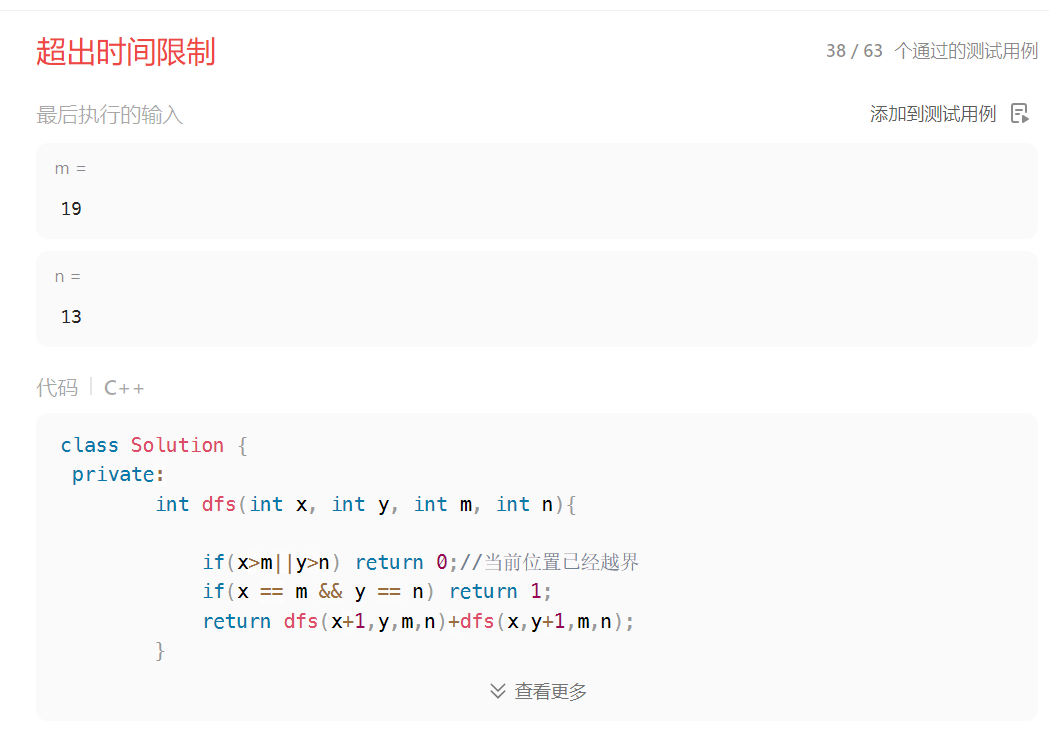
分析:因为整棵树的深度是
m+n-1.那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的
🦄动态规划解题思路:
- 1.确定dp数组及其下标含义:
dp[x][y]表示从(0,0)位置出发,到(x,y)位置的路径个数(求:dp[m-1][n-1]) - 2.确定递推公式:
题目说了,只能向下或向下走,那么从(0,0)到(x,y)位置的路径条数可以由这两个位置的路径条数相加得来,即:dp[x,y] = dp[x-1][y]+dp[x][y-1] - 3.dp数组如何初始化:
由于只能向右和向下走,那么可以确定的是,dp[x][0]和dp[0][y]都是为1for (int i = 0; i < m; i++) dp[i][0] = 1; for (int i = 0; i < n; i++) dp[0][i] = 1; - 4.dp数组的初始化顺序:
因为当前位置只能从左边和上面推导而来,所以这两个位置必须先确定,即:从左到右逐层往下遍历 - 5.举例推导dp数组
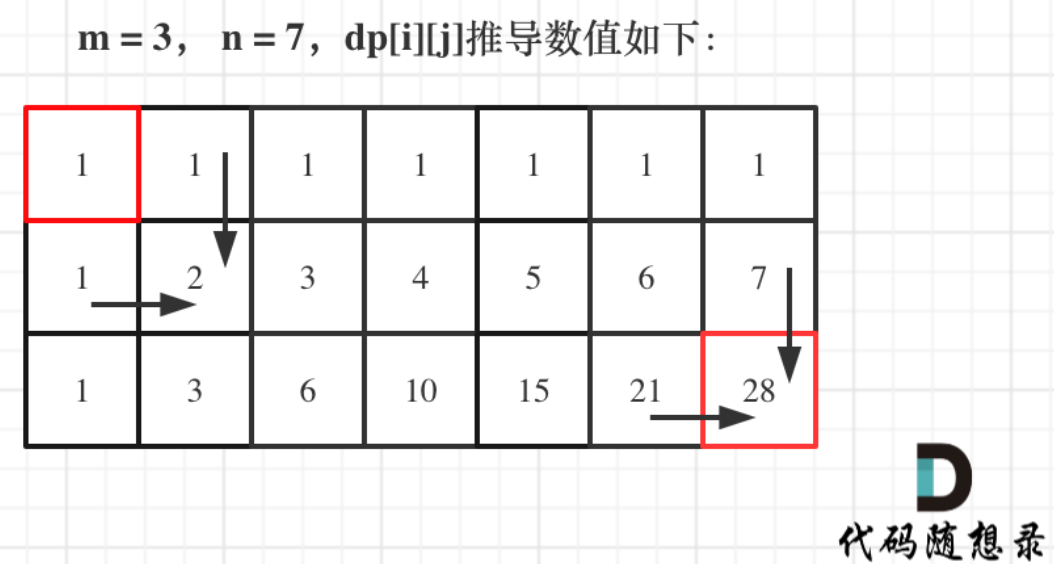
✅正确代码:
class Solution {
public:
int uniquePaths(int m, int n) {
vector < vector<int> > dp(m, vector <int>(n,0));
//初始化
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int i = 0; i < n; i++) dp[0][i] = 1;
//遍历
for (int i = 1 ; i < m; i++){
for (int j = 1; j < n; j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};
时间复杂度:
O(m*n)
63. 不同路径 II
题目链接
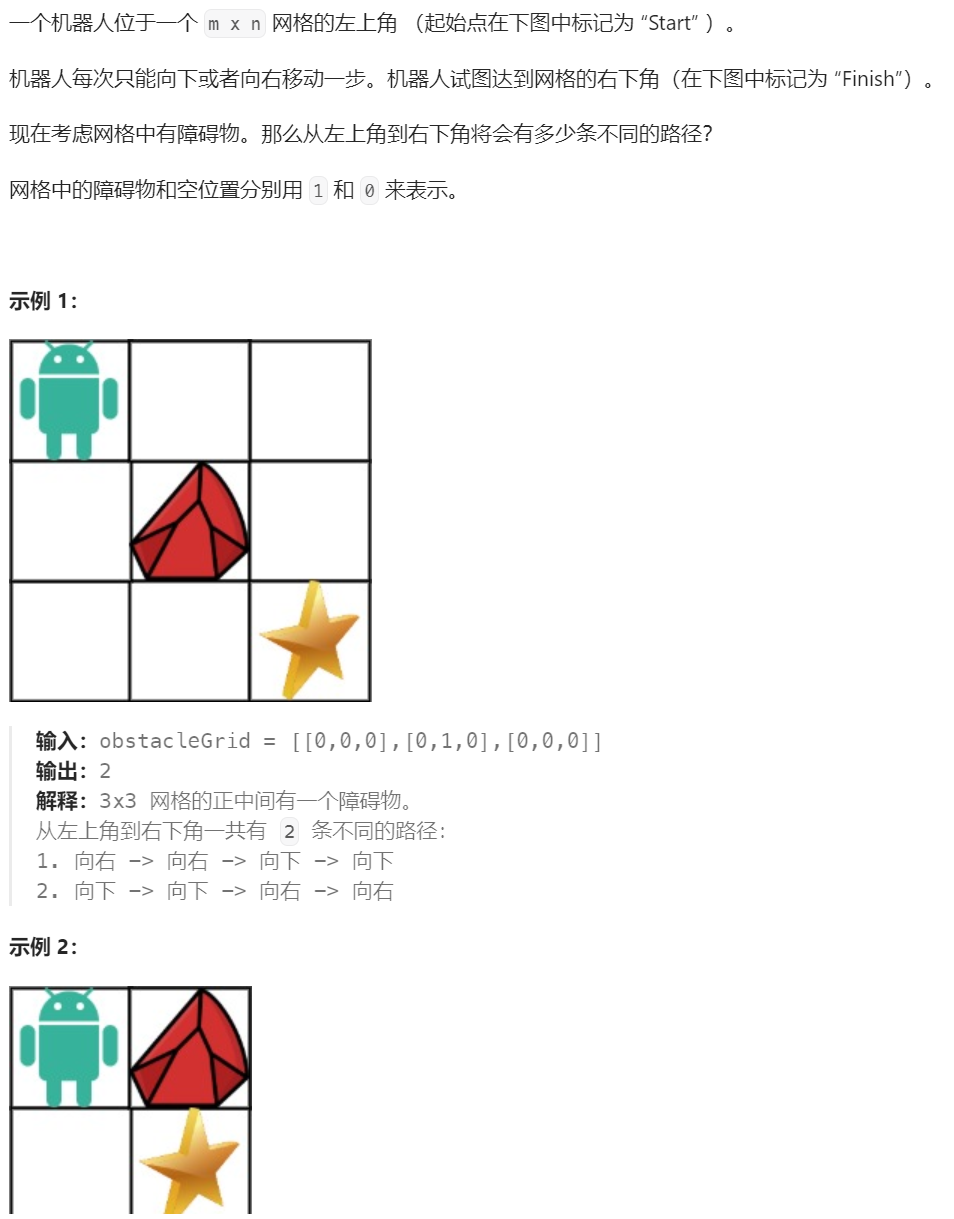
🦄动态规划解题思路:
这题与上题的整体思路还是一致的,加了障碍物会影响两个地方:
dp数组的初始化状态转移方程(实际上在代码上没影响)
✅正确代码:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector < vector<int> > dp(m, vector <int>(n,0));
//初始化
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[0][i] = 1;
//遍历
for (int i = 1 ; i < m; i++){
for (int j = 1; j < n; j++){
if (obstacleGrid[i][j] == 1) continue; //当前有障碍物,说明到不了这个位置,continue,使dp[i][j]保持为0
// if(obstacleGrid[i][j-1] == 1 && obstacleGrid[i-1][j] == 1){dp[i][j] = 0 ;continue;}
// if(obstacleGrid[i][j-1] == 1) {dp[i][j] = dp[i-1][j]; continue;}
// if (obstacleGrid[i- 1][j] == 1){dp[i][j] = dp[i][j-1]; continue;}
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};
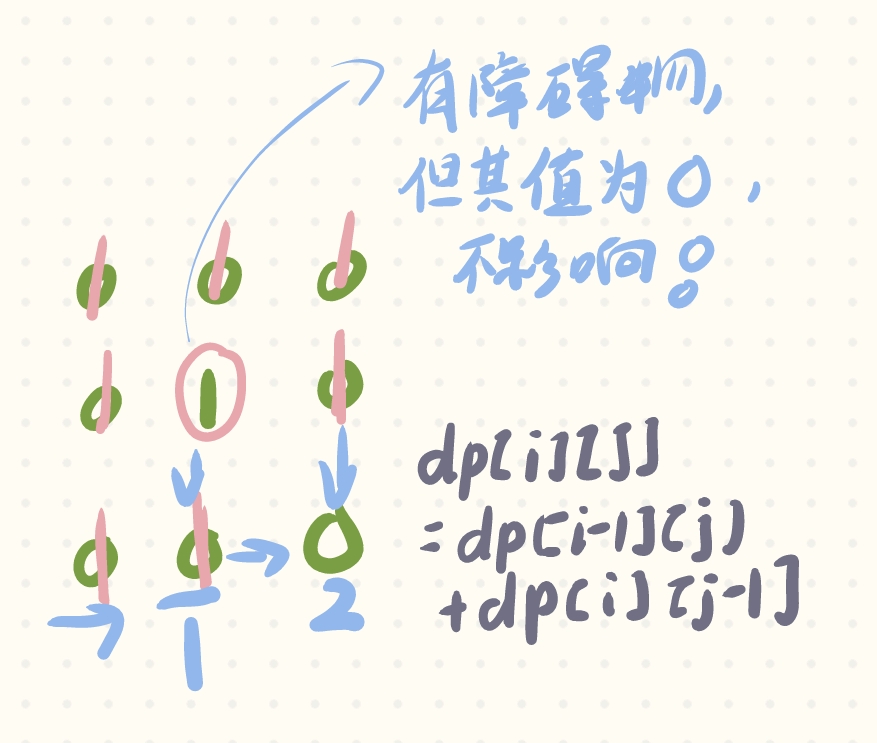
注释掉的代码加上也没有错,是因为我一开始认为状态方程根据前两个推到位置是否有障碍物需要做出改变。但是看到下图的推导过程,即使是障碍物,加上也是
0,其实也没事!






![[LeetBook]【学习日记】寻找和为指定数字的连续数字](https://img-blog.csdnimg.cn/direct/47f8162bd66e45c5a3ac63af13021b02.png)