鸿蒙Harmony应用开发—ArkTS声明式开发（通用属性：分布式迁移标识）

news2024/10/5 18:29:59

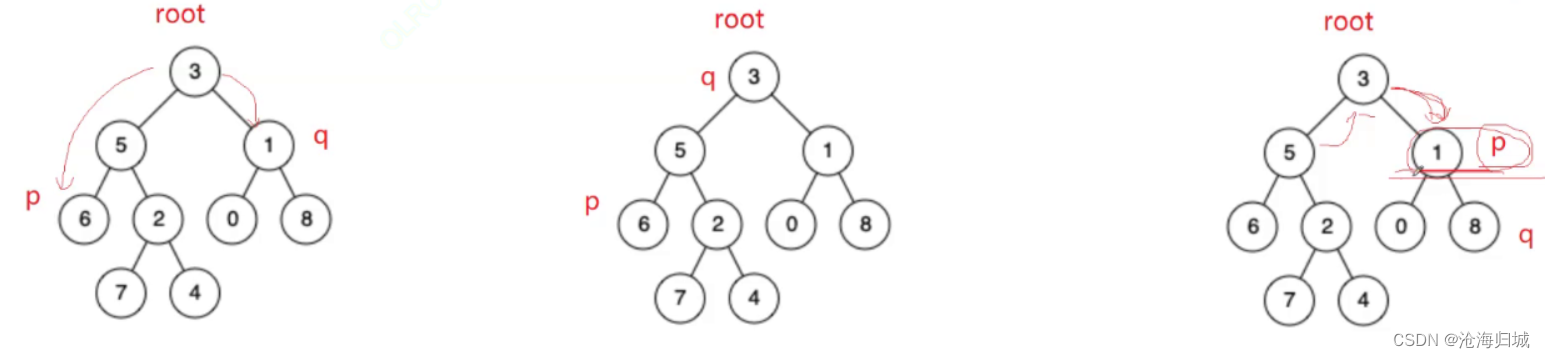
组件的分布式迁移标识，指明了该组件在分布式迁移场景下可以将特定状态恢复到对端设备。

说明：

从API Version 8开始支持。后续版本如有新增内容，则采用上角标单独标记该内容的起始版本。

restoreId

restoreId(value: number)

标记支持分布式迁移的组件Id，用于两端设备组件的配对。

系统能力： SystemCapability.ArkUI.ArkUI.Full

参数：

参数名	类型	必填	说明
value	number	是	标记支持分布式迁移的组件Id，用于两端设备组件的配对。同一个应用中各个支持分布式迁移组件的Id必须不同。

支持的组件

组件名称	起始版本	迁移状态
List	8	迁移当前设备显示在顶部ListItem的索引值，迁移后在对端设备上，将迁移索引值对应的ListItem在List中完整地置顶显示。
Grid	9	迁移当前设备显示在顶部GridItem的索引值，迁移后在对端设备上，将迁移索引值对应的GridItem在Grid中完整地置顶显示。ScrollBar位置无法迁移。
Scroll	9	迁移距顶部滚动的绝对距离。两端设备显示规格不同等原因导致布局不一致，会影响迁移效果。
WaterFlow	11	迁移当前设备显示在顶部FlowItem的索引值，迁移后在对端设备上，将迁移索引值对应的FlowItem在WaterFlow顶部显示。同时迁移顶部FlowItem相对WaterFlow的主轴偏移值（vp单位）。

示例

// xxx.ets
@Entry
@Component
struct RestoreIdExample {
  private arr: number[] = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
  build() {
    Column() {
      List({ space: 20 }) {
        ForEach(this.arr, (item:number) => {
          ListItem() {
            Text('' + item)
              .width('100%')
              .height(100)
              .fontSize(16)
              .textAlign(TextAlign.Center)
              .borderRadius(10)
              .backgroundColor(Color.Pink)
          }
        }, (item:number) => (item.toString()))
      }
      .restoreId(1)
    }
  }
}

最后，有很多小伙伴不知道学习哪些鸿蒙开发技术？不知道需要重点掌握哪些鸿蒙应用开发知识点？而且学习时频繁踩坑，最终浪费大量时间。所以有一份实用的鸿蒙（Harmony NEXT）资料用来跟着学习是非常有必要的。

这份鸿蒙（Harmony NEXT）资料包含了鸿蒙开发必掌握的核心知识要点，内容包含了（ArkTS、ArkUI开发组件、Stage模型、多端部署、分布式应用开发、音频、视频、WebGL、OpenHarmony多媒体技术、Napi组件、OpenHarmony内核、Harmony南向开发、鸿蒙项目实战等等）鸿蒙（Harmony NEXT）技术知识点。

希望这一份鸿蒙学习资料能够给大家带来帮助，有需要的小伙伴自行领取，限时开源，先到先得~无套路领取！！

获取这份完整版高清学习路线，请点击→纯血版全套鸿蒙HarmonyOS学习资料

鸿蒙（Harmony NEXT）最新学习路线

HarmonOS基础技能

HarmonOS就业必备技能
HarmonOS多媒体技术

鸿蒙NaPi组件进阶

HarmonOS高级技能

初识HarmonOS内核
实战就业级设备开发

有了路线图，怎么能没有学习资料呢，小编也准备了一份联合鸿蒙官方发布笔记整理收纳的一套系统性的鸿蒙（OpenHarmony ）学习手册（共计1236页）与鸿蒙（OpenHarmony ）开发入门教学视频，内容包含：ArkTS、ArkUI、Web开发、应用模型、资源分类…等知识点。

获取以上完整版高清学习路线，请点击→纯血版全套鸿蒙HarmonyOS学习资料