1.题目描述
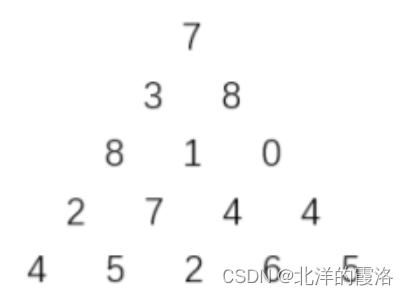
上图给出了一个数字三角形。
从三角形的顶部到底部有很多条不同的路径。
对于每条路径,把路径上面的数加起来可以得到一个和,你的任务就是找到最大的和。
路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。
此外,向左下走的次数与向右下走的次数相差不能超过 1。
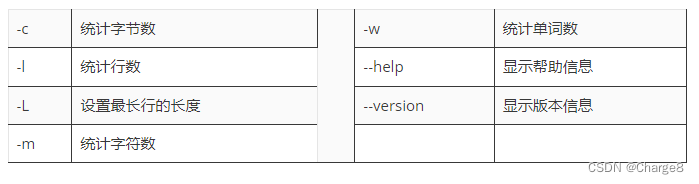
2.输入格式
输入的第一行包含一个整数 N,表示三角形的行数。
下面的 N 行给出数字三角形。
数字三角形上的数都是 0 至 100 之间的整数。
3.输出格式
输出一个整数,表示答案。
4.数据范围
1≤N≤100
5.输入样例
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
6.输出样例
27
7.思路
动态规划
1.状态表示 :f[i][j]表示所有从头开始往下走到第i层第j个的路径的最大值
2.状态计算 :f[i][j] = max(f[i-1][j],f[i-1][j-1]) + value[i][j];
8.代码
#include<iostream>
using namespace std;
const int N = 110;
int n;
int f[N][N];
int value[N][N];
int main()
{
scanf("%d",&n);
for(int i = 1; i<=n; i++)
for(int j = 1; j <=i; j++)
scanf("%d",&value[i][j]);
for(int i = 1; i<= n; i++)
for(int j = 1; j <=i; j++)
f[i][j] = max(f[i-1][j],f[i-1][j-1]) + value[i][j];
//n为偶数时,最后一层落在的点一定在n/2或n/2+1
//n为奇数时,最后一层落在的点一定在n/2+1
if(n % 2 == 0) printf("%d\n", max(f[n][n/2],f[n][n/2+1]));
else printf("%d\n", f[n][n/2+1]);
return 0;
}