题目描述
题目链接:2369.检查数组是否存在有效划分
描述:
给你一个下标从 0 开始的整数数组 nums,你必须将数组划分为一个或多个连续子数组。如果获得的这些子数组中每个都能满足下述条件 之一 ,则可以称其为数组的一种有效划分:
- 子数组 恰 由 2 个相等元素组成,例如子数组 [2,2] 。
- 子数组 恰 由 3 个相等元素组成,例如子数组 [4,4,4] 。
- 子数组 恰 由 3 个连续递增元素组成,并且相邻元素之间的差值为 1 。例如子数组 [3,4,5] ,但是子数组 [1,3,5] 不符合要求。
如果数组至少存在一种有效划分,返回 true ,否则,返回 false 。
输入输出描述
示例 1:
输入:nums = [4,4,4,5,6] 输出:true 解释:数组可以划分成子数组 [4,4] 和 [4,5,6] 。 这是一种有效划分,所以返回 true 。
示例 2:
输入:nums = [1,1,1,2] 输出:false 解释:该数组不存在有效划分。
解题思路
状态定义:
如果 nums的最后两个数相等,那么去掉这两个数,问题变成剩下 n−2个数能否有效划分。
如果 nums的最后三个数相等,那么去掉这三个数,问题变成剩下 n−3个数能否有效划分。
如果 nums的最后三个数是连续递增的,那么去掉这三个数,问题变成剩下 n−3个数能否有效划分。最终解决问题:nums的前i个数能否有效划分。
边界条件:f[0] = true, f[i+1]表示能否有效划分nums[0]到nums[i]。所以可以推到其动态方程为:
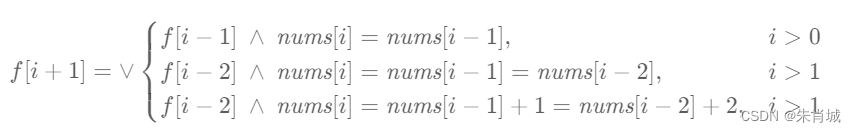
动态规划的教程也在编写,可以参考:【动态规划专栏】-CSDN博客
复杂度分析
时间复杂度:O(n),其中n为nums的长度
空间复杂度:O(n)
代码
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
bool validPartition(vector<int> &nums) {
int n = nums.size();
vector<int> f(n + 1);
f[0] = true;
for (int i = 1; i < n; i++) {
if (f[i - 1] && nums[i] == nums[i - 1] ||
i > 1 && f[i - 2] && (nums[i] == nums[i - 1] && nums[i] == nums[i - 2] ||
nums[i] == nums[i - 1] + 1 && nums[i] == nums[i - 2] + 2)) {
f[i + 1] = true;
}
}
return f[n];
}
};
int main()
{
vector<int> nums = {4, 4, 4, 5, 6};
bool res = Solution().validPartition(nums);
cout << "res0: " << res << endl;
nums = {1, 1, 1, 2};
res = Solution().validPartition(nums);
cout << "res1: " << res << endl;
}