计算机视觉基础知识(一)--数学基础

news2024/9/22 15:29:31

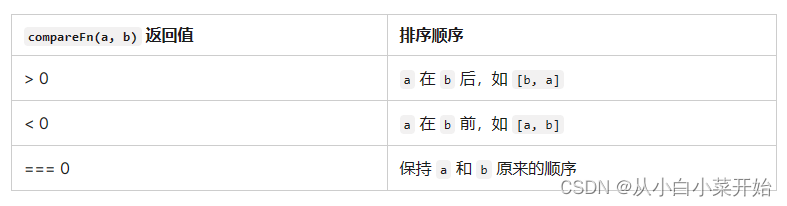
向量

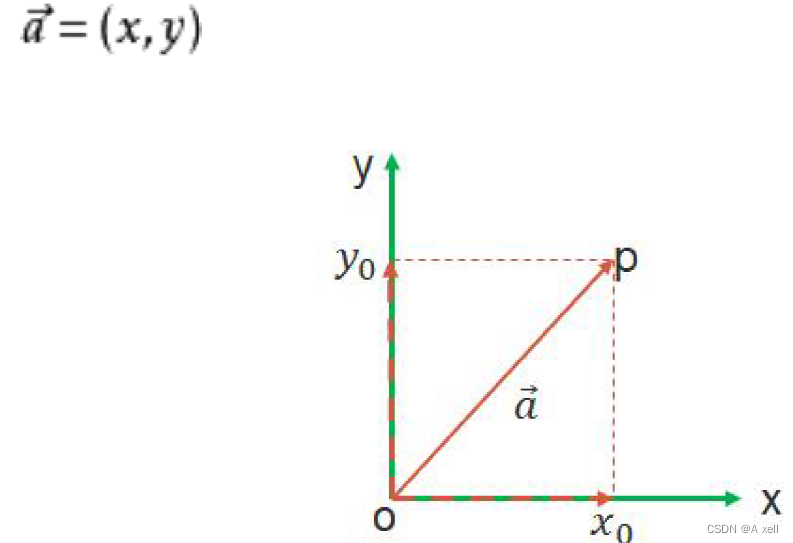
线性变换

矩阵

充满数字的表格

矩阵加减法

要满足两个矩阵的行数与列数一致;
加法交换律:A+B=B+A

矩阵乘法

要满足A的列数等于B的行数;

单位矩阵

是一个nxn矩阵;
从左到右对角线上的元素值为1;
其余元素为0;
A为nxn矩阵,I为单位矩阵, $AI=A,IA=A$ ;
单位矩阵在乘法中的作用相当于数字1;

逆矩阵

矩阵A的逆矩阵记做 $A^{-1}$ ;
$A\cdot A^{-1}=A^{-1}A=I$ ;
I是单位矩阵

奇异矩阵

没有逆矩阵的矩阵称为奇异矩阵;
当且仅当矩阵的行列式为零时,该矩阵奇异;

当ad-bc=0, $|A|$ 没有定义, $A^{-1}$ 不存在,A奇异;

矩阵转置

行列互换;
用 $A^T$ 表示;

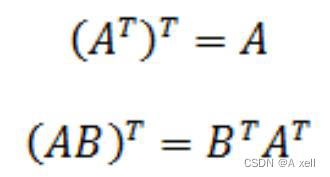
对称矩阵

等于转置矩阵的矩阵为对称矩阵;
矩阵的转置乘以矩阵结果为对称矩阵;

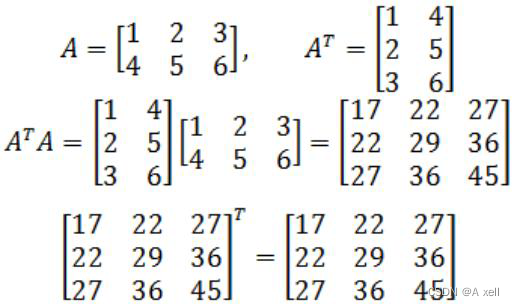
欧式变换

旋转
平移

$a'=Ra+t$

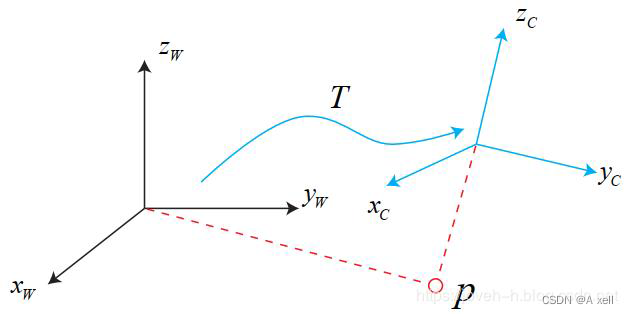
齐次坐标

用N+1维代替N维坐标;
2D齐次坐标:在2D坐标的末尾加上一个额外的变量w;
点 $(X,Y)$ 的齐次坐标为: $(x,y,w)$ ;
有: $X=x/w,Y=y/w$

$(x,y,w)_{Homogeneous}\Rightarrow (\frac{x}{w},\frac{y}{w})_{Cartesian}$

点 $(1,2)$ 的齐次坐标为: $(1,2,1)$ ;
如果点 $(1,2)$ 移动到无限远处;
在笛卡尔坐标下变为: $(\infty ,\infty)$ ;
他的齐次坐标表示为: $(1,2,1)$ ;
因为: $(1/0,2/0)=(\infty,\infty)$ ;

导数(微分)

代表函数(曲线)的斜率;
描述函数(曲线)变换快慢的量;
可判断曲线的极大值点,导数为零的点,斜率为0;

偏导数

多元函数的情况下;
对每个变量求导;
暂时把其他变量看做常量;
意义为查看在其他变量不变的情况下该变量对函数的影响程度;

梯度

本意是一个向量(矢量);
表示某一函数在该点处的方向导数沿着该方向取得最大值;
函数在该点处沿着该方向(梯度的方向)变化最快;
对多元函数的各自变量求偏导,并写成向量形式,就是梯度;

梯度下降法

一种寻找函数极小值的方法;
在参数当前值已知的情况下;
按照该点梯度向量的反方向;
按事先给定好的步长;
对参数进行调整;
多次调整参数后;
函数会逼近一个极小值;

梯度下降法存在的问题

参数调整缓慢;
收敛于局部最小值;

概率基础

机器学习与传统统计分析的区别在于:
关注的主体和验证性;
机器学习不关系模型的复杂度的高低;
仅要求模型有良好的泛化性及准确性;
传统的统计分析对模型有一定的要求;
模型不可过于复杂;

事件关系运算

事件运算定律

交换律: $A\bigcup B=B\bigcup A,A \bigcap B=B\bigcap A$ ;
结合律: $(A\bigcup B)\bigcup C=A\bigcup(B\bigcup C),(A\bigcap B)\bigcap C=A\bigcap(B\bigcap C)$ ;
分配率: $(A\bigcup B)\bigcap C=(A\bigcap C)\bigcup (B\bigcap C)$ ;

概率基本概念

事件发生的可能性大小的度量;
对任何事件A,P(A)>=0;
对必然事件B,P(B)=1;
事件g的概率P(g),在事件集合上满足上述两个条件;

概率的基本性质

$P(\overline{A})=1-P(A)$ ;
$P(A-B)=P(A)-P(AB)$ ;

古典型概率

实验的所有结果只有有限个;
每个结果发生的可能性相同;
P(A)=事件A发生的基本事件数/基本事件总数;

独立性

A,B为随机事件;
若同时发生的概率等于各自概率的乘积;
A,B相互独立;

$P(AB)=P(A)P(B)$

离散

不连续

数学期望(均值)

表示一事件平均发生的概率;
记为 $E(x)$ ;
$E(x)=x_1p_1+x_2p_2+...+x_np_n$ ;
或者: $E(x)=\int_{-\infty}^{\infty}xf(x)dx$

方差

刻画随机变量x;
和数学期望E(x);
之间偏离的程度;
记为D(x);

标准差(均方差)

方差的算术平方根;
反映一个数据集的离散程度;

正态分布(高斯分布)

随机变量x;
服从数学期望为 $\mu$ ,方差为 $\sigma^2$ 的正态分布;
记为 $N(\mu,\sigma^2)$ ;
$\mu$ 据定了对称中心线的位置;
标准差 $\sigma^2$ 决定分布的幅度(胖瘦);

标准正态分布

$\mu=0,\sigma=1$ ;
的正态分布为标准正态分布;

熵

物理学上为混乱程度的度量;
系统越有序,熵值越低;
系统越分散,熵值越高;

信息理论

系统的有序状态一致;
数据越集中的地方熵值越小;
数据越分散的地方熵值越大;
上述为从信息完整性方面的描述;
数据量一致;
系统越有序,熵值越低;
系统越分散,熵值越高;
以上是从信息的有序性上进行的描述;
不确定性越大,信息量越大,熵值越大;
不确定性越小,信息量越小,熵值越小;

信息熵

事件Ade分类划分为: $A_1,A_2,...,A_n$ ;
每部分发生的概率为: $p_1,p_2,...,p_n$ ;
信息熵的定义如下式:

$Ent(A)=-\sum^n_{k=1}p_klog_2 p_k$

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1487736.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！