参考：
[1] https://zhuanlan.zhihu.com/p/597490389
[2] https://www.zhangzhenhu.com/aigc/Score-Based_Generative_Models.html

1 基于分数的生成模型

1.1 简介和动机

所谓的分数就是对数概率密度的梯度，既$s(x)=\frac{\partial (logp(x))}{\partial x}$。我们很难估计真实数据分布$p(x)$，但如果我们知道分数， 就可以利用分数从$p(x)$做到随机采样，采样方法有很多。

分数就是梯度，既数据分布增大最大的方向和大小（梯度定义），对于数据概率分布来说，概率密度大的地方肯定就是我们想让模型采样数据的区域了（说明训练的图像所在分布都在附近），所以我们每次采样过程都沿着分数（梯度）的方向去走，那么最后就能走到数据分布的高概率区域，生成的数据样本也就符合原始数据分布了。

那么我们的优化目标是什么？以及我们如何采样呢？

1.2 Score Matching及其改进

1.2.1 Score Matching

分数匹配简单来说就是一种概率密度的估计方法。我们的优化目标可表示为下面式子，其中$s(x)=\frac{\partial (logp(x))}{\partial x}$
$$\frac{1}{2}{E}_{p_{data}(x)}[||s_{\theta }(x)-s_{data}(x)|{|}^2]$$
但是求真实的分数我们就要知道真实分布的概率密度，所有有一种score matching的方法可以巧妙地避过求真实分布的概率密度，推导如下图：

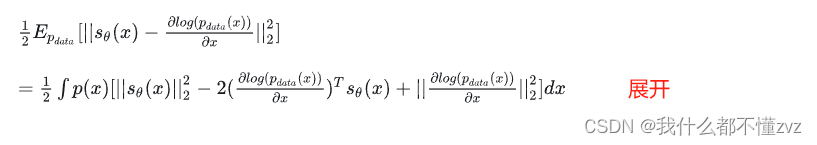
其中第三项不是关于$\theta$的，可以视作常数项。对于第二项，有如下化简：

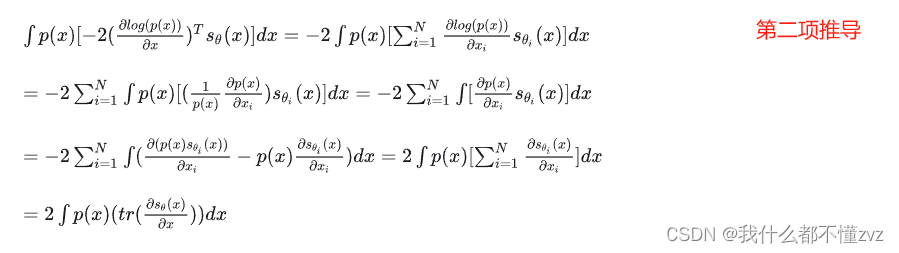
其中第二行、第三行的变换用到了分部积分，第三行直接写为$p(x)s_{{\theta }_i}(x){|}_{-\infty }^{\infty }$，积分默认是从负无穷到正无穷，且假设$p(\infty )=0$,最后合并，即可得到

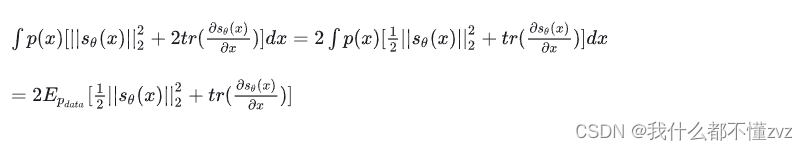
我们的优化目标经过score matching之后变为：
$$E_{p_{data}(x)}[tr(\frac{\partial s_{\theta }(x)}{\partial x})+\frac{1}{2}||s_{\theta }(x)|{|}^2]$$
其中偏导为$s_{\theta }(x)$的雅可比矩阵，tr为迹，也就是对角线之和。但由于是偏导数，所以需要多次反向传播来分别对每个分量进行计算。

1.2.2 Sliced score matching（不是主流，简单介绍）

我们使用一个对迹的估计方法（ Hutchinson trace estimator）对其进行估计，并且使用自动微分对最终形式进行计算：

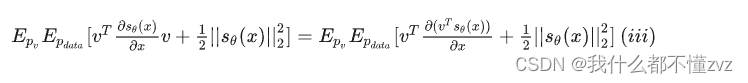
虽然更好计算了，但是计算量反增不减

1.2.3 Denoising Score Matching

之前说$p_{data}(x)$不知道，我们可以自定义数据分布，使之是被知道的。具体做法是：
对原始数据加上噪声，使之满足预定好的分布，然后就知道概率密度了，就可以使用最原始的方法去计算优化目标了。

假设预定好的分布（加噪过程）为$q_{\sigma }(\tilde{x}|x)=N(\tilde{x};x,{\sigma }^{2}I)$，其中$\sigma$是与定义好的。加噪的数据变为：$q_{\sigma }(\tilde{x})=\int q_{\sigma }(\tilde{x}|x)p_{data}(x)dx$，且在忽略与模型参数不相关的常数项后，我们可以得到：

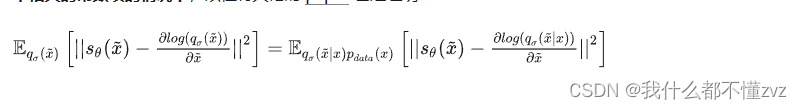
其中左边为显示分数匹配（EMS），右边为去噪分数匹配（DMS)。注意：此时我们传入到模型的是加噪后的数据$\tilde{x}$，加载过程就是从$N(0,I)$随机采样噪声，乘上预定义的方差，再加到样本中，既$\tilde{x}=x+\sigma ϵ$。这样加载后的数据会满足预定义好的$q_{\sigma }(\tilde{x}|x)$。我们网络估计出来的分数是对应噪声数据分布$q_{\sigma }(\tilde{x})$的，而非$p_{data}(x)$的，所以就要求$\sigma$很小，避免过大扰动。

所以经过denoising score matching可得优化目标：
$$\frac{1}{2}{E}_{q_{\sigma }(\tilde{x}|x)q_{data}(x)}[||s_{\theta }(\tilde{x})+{\nabla }_{\tilde{x}}log(q_{\theta }(\tilde{x}|x)|{|}^2]$$

1.3 朗之万动力学采样

采样过程如下：
$${\tilde{x}}_t={\tilde{x}}_{t-1}+\frac{ϵ}{2}{\nabla }_{{\tilde{x}}_{t-1}}logp({\tilde{x}}_{t-1})+\sqrt{ϵ}{z}_t$$
其中$z_t$为从N(0,1)采样的随机项，$ϵ$为预定好的的步长

1.4 问题

1.4.1 分数估计不准

流形学习角度

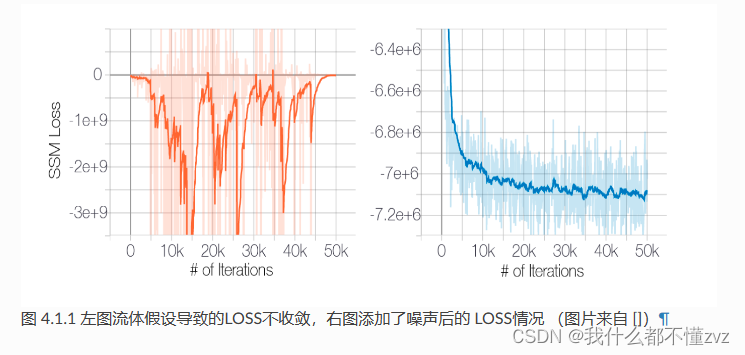
分数的估计$s(x)=\frac{\partial log(p_{data}(x)}{\partial x}$是针对整个编码空间定义的，根据mainfold hypotheis，高维空间中的真实数据大部分倾向于分布在低维空间，也就是说，在某些空间计算梯度是没有意义的，也就导致了loss震荡不收敛的情况。

低密度概率区域角度

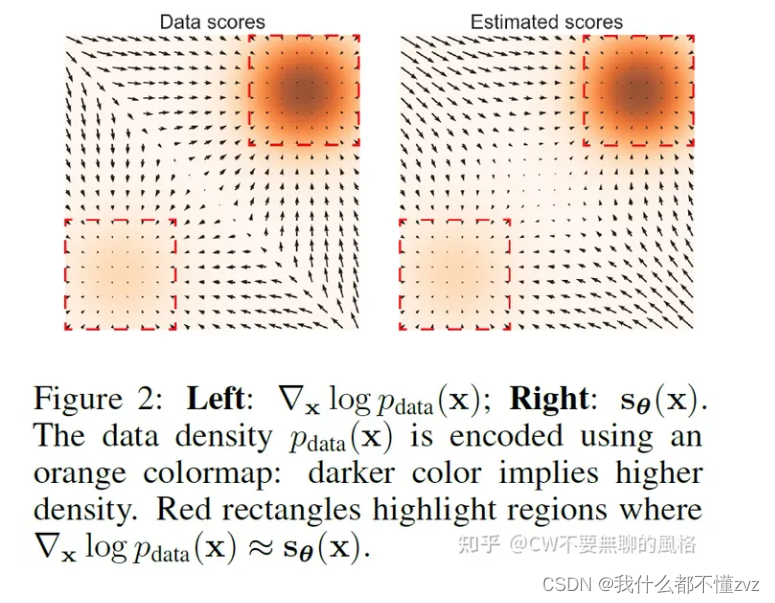
说白了就是模型训练不充分，属于低概率密度区域的数据没有足够的样本让模型去训练，所以导致这部分的分数估计不准。由上图右图可以知道，在中间低概率密度区域，梯度大小和左图真实分数不一样，对于右图而言，如果在中间的地概率密度区域采样，那么可能就陷入在这了（梯度大小太小，不更新）

1.4.2 生成结果偏差大

我们采用的郎之万动力学采样有一个缺陷，当低密度区与把概率空间分成几块的时候，郎之万动力学采样不能很好地表示其比例关系（如下不严谨推导）

理论上当步长很小，步数很大的时候可以得到与原分布相似的结果，但通常不这么做，太费劲。

2 NCSN模型

2.1 为什么NCSN模型可以

之前提到了两个困难：1） 高维空间的有效性，既真实数据往往只集中在少数低维空间；2）低密度区域往往因为训练样本不足导致分数匹配估计不准确；

通过添加高斯噪声可以解决以上困难：
1） 增加高斯噪声后，相当于改变了原数据分布。首先会破坏$x$各个维度的相关性，使之的相关性逐渐减少，相当于$x$变成了满秩。也就解决了上面说的流形学习的问题。
2） 各个分量之间添加的噪声是同等权重的，所以低密度区域的密度会变大，整个密度空间也就变得均匀。且低密度区域不仅会被填满，高密度区域所占的比例在填满后会变得更高，所以扰动后的分数更多地由比例更高的分布的分数演变而来，所以分数的方向自然就指向比例更高的分布。我的理解是以下$p_1(x)$的值更大了，而$p_2(x)$的值还很小。

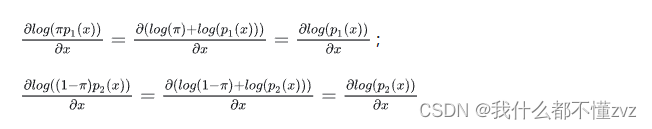
2.2 NCSN模型详解

2.2.1 噪声设计原则

上面说到，添加高斯噪声可以解决提到的两个困难，并且噪声强度越大，解决的效果越明显。但我们也知道，去噪分数匹配的前提就是$q_{\sigma }(\tilde{x})$不能离$p_{data}(x)$太远，所以添加的噪声强度不能太大。所以作者设计了各种强度的噪声， { σ i } i = 1 L \{\sigma_i\}_{i=1}^L {σi​}i=1L​满足$\frac{{\sigma }_1}{{\sigma }_2}=...=\frac{{\sigma }_{L-1}}{{\sigma }_L}>1$，且${\sigma }_1$足够大，使得能够填充低密度区与，${\sigma }_L$足够小，使得对原数据分布良好近似

2.2.2 去噪分数匹配

我们已知$q_{\sigma }(\tilde{x})$满足高斯分布$N(x,{\sigma }^{2}I)$，所以其分数$\nabla log(q_{\sigma }(\tilde{x}|x))=-(\frac{\tilde{x}-x}{{\sigma }^2})$，所以某个噪声级别的优化目标可以变为：
$$l(\theta ;\sigma )=\frac{1}{2}{E}_{p_{data}}{E}_{\tilde{x}\sim N(x,{\sigma }^{2}I)}[||s_{\theta }(\tilde{x},\sigma )+\frac{\tilde{x}-x}{{\sigma }^2}|{|}^2]$$

又NCSN使用了多个噪声级别，应该对齐损失加权后在求平均，所以
$$L=\frac{1}{L}\sum \lambda ({\sigma }_i)l(\theta ;\sigma )$$

$\lambda$该如何设计呢，有以下出发点：
1） 所有加权后的噪声都应该在同一个数量级，既不受$\sigma$影响，这样就不会因为加权后哪个噪声级别大或小，就重视或忽略其他级别噪声。

作者发现$s_{\theta }(\tilde{x},\sigma )$的L2范数在$\frac{1}{\sigma }$的水平，所以作者将$\lambda (\sigma )$设为${\sigma }_i^2$，代入后得

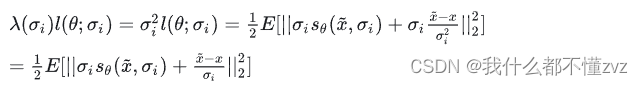
所以term 1的量级会变为1， term 2采样自$N(0,I)$,所以所有噪声级别的损失都会在同一量级。

2.2.3 退火朗之万动力学采样

前文我们讨论过，郎之万动力采样法存在着不足，对于那些存在低密度区域分割成多个高密度区域的复杂分布，需要较多的采样步骤才能得到相对可靠的采样结果， 无法在一个可接受的步骤内得到较好的采样结果，针对这个问题，作者提出了一个改进的郎之万动力采样法，称为退火朗之万动力采样法 （annealed Langevin dynamics）。之所以叫退火朗之万动力采样法，是因为每次的噪音级别都在减小，所以annealed。

首先初始化超参 { σ i } \{\sigma_i\} {σi​}，然后从均匀分布或高斯分布中随机采样初始化${\tilde{x}}_0$。第一层循环是噪声等级循环，由${\sigma }_1$到${\sigma }_L$,由大到小。内部循环是一个朗之万动力学采样过程，既步数由1到T，传入${\tilde{x}}_{t-1}、{\sigma }_i$到模型中，预测出分数，然后代入式子进行采样。并且每次内部循环以后，下一个级别的噪声会用上一个级别噪声计算出来的${\tilde{x}}_0$来当作初始化噪声，理由在下面会解释。当$i=L$时，${\sigma }_L$很小，所以最终得到的分布就近似于真实数据分布

为什么要用上一个级别的噪声来计算呢？


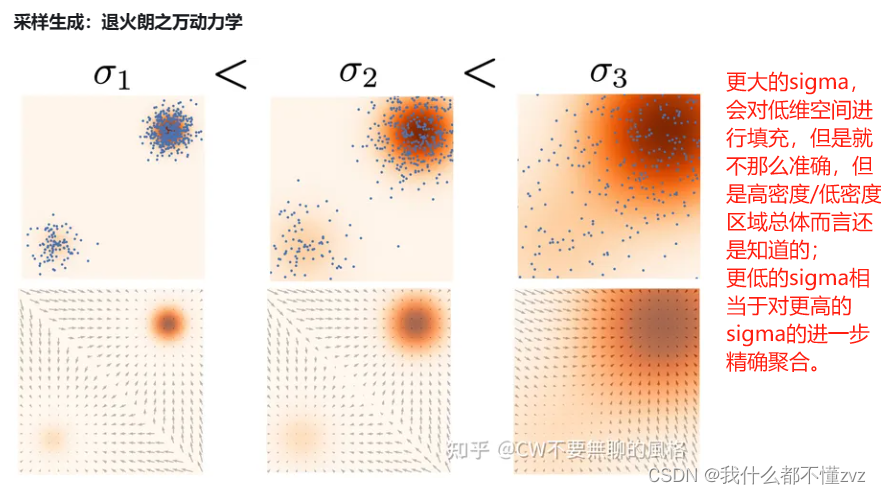
这里$\alpha =ϵ\frac{{\sigma }_i^2}{{\sigma }_L^2}$的设计是因为：

2.2.4 模型设计

模型的输出（分数）要和模型的输入图像的shape保持一致，很自然就想到用UNet模型。作者还在其中加入了空洞卷积和以噪声为条件的实例归一化（conditional instance normalization ++ )，并且对于同一个像素点，不同强度下的噪声强度也要对应估计出不同的分数，所以模型还要以噪声强度${\sigma }_i$作为输入。

2.3 结合代码具体理解：

2.3.1 Loss

NCSN的损失函数可以表示为：

$$l(\theta ;\sigma )=\frac{1}{2}{E}_{p_{data}}{E}_{\tilde{x}\sim N(x,{\sigma }^{2}I)}[||s_{\theta }(\tilde{x},\sigma )+\frac{\tilde{x}-x}{{\sigma }^2}|{|}^2]$$
又
$$\begin{gathered} L=\frac{1}{L}\sum \lambda ({\sigma }_i)l(\theta ;\sigma ) \\ \lambda (\sigma )={\sigma }^2 \end{gathered}$$
代码及其解析：

def anneal_dsm_score_estimation(scorenet, samples, labels, sigmas, anneal_power=2.):
    used_sigmas = sigmas[labels].view(samples.shape[0], *([1] * len(samples.shape[1:])))
    
    perturbed_samples = samples + torch.randn_like(samples) * used_sigmas
    
    target = - 1 / (used_sigmas ** 2) * (perturbed_samples - samples)
    
    scores = scorenet(perturbed_samples, labels)
    target = target.view(target.shape[0], -1)
    scores = scores.view(scores.shape[0], -1)
    
    loss = 1 / 2. * ((scores - target) ** 2).sum(dim=-1) * used_sigmas.squeeze() ** anneal_power
    return loss.mean(dim=0)

• 传入的参数分别表示：
  1）scorenet： 预测分数的网络
  2）samples： 采样的样本，加噪前的样本，既$x_{t-1}$
  3）labels： 噪声的级别，可以理解为$i$，相当于索引，就是能够区分不同的噪声即可
  4）sigmas：预定义的方差
  5）annel_power：就是$\lambda ={\sigma }^2$中的平方项

• 第一行代码将尺寸由(bs,)变为(bs,1,1,1)

• 第二行代码计算 $\tilde{x}=x+\sigma ϵ$

• 第三行代码计算 $\frac{\tilde{x}-x}{{\sigma }^2}$

• 第四行代码计算模型预测的分数

• 第五行、第六行代码将尺度变换以下方便计算loss

• 第七行计算loss，首先计算所有维度下的分数估计的误差总和，然后再求平均

2.3.2 采样生成

伪代码如下：

python代码如下：

def anneal_Langevin_dynamics(self, x_mod, scorenet, sigmas, n_steps_each=100, step_lr=0.00002):
    images = []

    with torch.no_grad():
        # 依次在每个噪声级别下进行朗之万动力学采样生成，噪声强度递减
        for c, sigma in tqdm.tqdm(enumerate(sigmas), total=len(sigmas), desc='annealed Langevin dynamics sampling'):
            # 噪声级别
            labels = torch.ones(x_mod.shape[0], device=x_mod.device) * c # 
            labels = labels.long()

            # 这个步长并非 Algorithm 1 中的 alpha，而是其中第6步的 alpha/2
            step_size = step_lr * (sigma / sigmas[-1]) ** 2
            
            # 每个噪声级别下进行一定步数的朗之万动力学采样生成
            for s in range(n_steps_each):
                images.append(torch.clamp(x_mod, 0.0, 1.0).to('cpu'))
                # 对应公式(vi)最后一项
                noise = torch.randn_like(x_mod) * np.sqrt(step_size * 2)
                # 网络估计的分数
                grad = scorenet(x_mod, labels)
                # 朗之万动力方程
                x_mod = x_mod + step_size * grad + noise

        return images

• x_mod：${\tilde{x}}_0$
• 外部for循环中的c表示索引，而labels就是索引值
• step_size表示${\alpha }_i/2$，而${\alpha }_i=ϵ\ast {\sigma }_i/{\sigma }_L$，其中$ϵ=0.00002$
• 内部循环中，要将images先裁剪到0~1,是因为：
  1）方便后期变换为0-255
  2）模型兼容性：归一化到0-1，后期采样时对模型归一化就具有意义。
  3）可视化和存储：将图像数据裁剪到0到1的范围内可以直接用于可视化或存储为标准格式的图像文件（如JPEG或PNG），这些格式期望输入数据在这个范围内。

2.3.3 ConditionalNorm