一、基本理解
枚举的概念就是把满足题目条件的所有情况都列举出来,然后一一判定,找到最优解的过程。
枚举虽然看起来麻烦,但是有时效率上比排序高,也是一个不错的方法、
二、最值问题
1、两个数的最值问题
两个数的最小值,利用C语言中的三元运算符就可以实现:
int Min(int a, int b) {
return a < b ? a : b;
}
2、n 个数的最值问题
当有 n 个数时 ai 时,我们可以首先取前两个数,计算最小值;然后再拿这个最小值和第三个数去比较,得到的最小值再去和第四个数比较,以此类推,就可以计算出 n 个数中的最小值。
假设前 i 个数的最小值为 mi,则有递推公式如下:
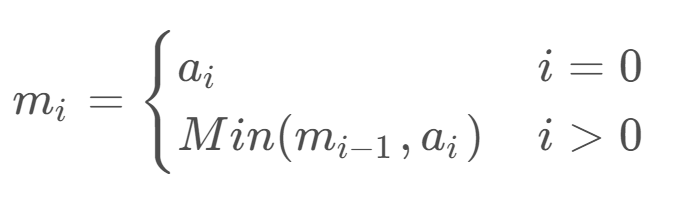
所以,把这个递推公式翻译成C语言,代码是这样的:
int Min(int a, int b) {
return a < b ? a : b;
}
int NMin(int* a, int n){
int *m = (int *) malloc( sizeof(int) * numsSize );
int m[0] = a[0];
for(int i = 1; i < n; ++i) {
m[i] = Min(m[i-1], a[i]);
}
int ret = m[n-1];
free(m);
return ret;
}
而这里的 m[i] 和 m[i-1] 可以利用迭代,存储在一个变量中,用 C语言实现如下:
int Min(int a, int b) {
return a < b ? a : b;
}
int NMin(int* a, int n){
int m = a[0];
for(int i = 1; i < n; ++i) {
m = Min(m, a[i]);
}
return m;
}
3、最值问题的下标
当然,有些时候,我们求的并不是一个最小的数,要是要求出这个数组中,最小的数的下标,那么可以直接记录下标,并且比较的时候直接通过下标去索引到值,然后进行比较,像这样:
int NMin(int* a, int n){
int mIdx = 0;
for(int i = 1; i < n; ++i) {
if( a[i] < a[mIdx] ) {
mIdx = i;
}
}
return mIdx;
}
可以尝试做一下这道题,巩固一下概念:https://leetcode.cn/problems/maximum-sum-with-exactly-k-elements/
三、最值问题的进阶
1、第三大的数
有时候,我们求最大的数不够,想要求次大的,甚至第三大的,比如 1 2 2 3 中第三大的是 1 (相同的数只计算一次)。
这样的问题,核心思路就是先把最大的求出来;然后忽略最大的数的情况下,再去求最大的;这时候就得到了次大的,再把次大的也忽略以后,再求最大的,自然就是第三大的了。
第三大的数 - 视频讲解。
2、数组中两元素的最大乘积
要求找到数组中两个元素的最大乘积,数组元素一定是正数。那么我们知道最大的两个元素相乘一定是最大的,所以就是找最大的元素 和 次大的元素,但是这个问题和 第三大的数 略微有些不同,相同的数会被计算进去。
所以,我们找到最大的数以后,可以把它的下标忽略掉;然后再去找最大的数,这样找到的一定是两个可重复的最大元素和次大元素,将两者相乘即可。
当然有同学就要问了,那我是不是直接把数组按照递增排序,然后取最后两个元素相乘就可以了。是的,也可以,但是比较排序的最优时间复杂度为 O(nlogn),而找两次最大值的时间复杂度为 O(n)。
四、降维思想
一些统计类问题,第一个思路就是枚举所有情况(也就是多个 for 循环),然后再去考虑是不是能够把某些 for 循环的 O(n) 的时间复杂度降为 O(1),这个就是降维的思想。来看这个经典问题:
这个问题能自己想出来,就达到了 ACM 区域赛铜牌的水平。
给你一个长度为 n (n ≤ 4000) 下标从 0 开始的整数数组 nums ,它包含 1 到 n 的所有数字,请你返回上升四元组的数目。如果一个四元组 (i, j, k, l) 满足以下条件,我们称它是上升的:
1)0 <= i < j < k < l < n 且
2)nums[i] < nums[k] < nums[j] < nums[l] 。
1、O(n^4)
首先,最坏时间复杂度的算法,相信大家都能想出来,就是枚举 i、j、k、l 四个变量,然后判断 nums 四个数的关系,进行统计累加,这种情况下,最坏的时间复杂度为 O(n^4),由于 n 为 4000。
也就是相当于 n = 16000000 的数据量下,用 O(n^2) 的算法去求解问题,所以必然超时。
2、O(n^3)
如果要用 O(n^3) 的算法求解,你会怎么去思考呢?如果有想法,可以写好以后附在评论区。
3、O(n^2)
是的,由于 n 的范围限制, 就算你想出了 O(n^3) 的算法,还是过不了这个问题,我们需要继续想 O(n^2) 的算法。
算法思路如下:
1、首先,我们枚举 j 和 k,然后对所有满足 nums[j] > nums[k] 的下标对,执行下一步。
2、那么只要我们找到数组下标为 0 到 j-1 的数中,小于 nums[k] 的个数,记为 a(也就是所有满足条件的 i); 找到数组下标为 k+1 到 n-1 的数中,大于 nums[j] 的个数,记为 b(也就是所有满足条件的); 将 a * b 就是所有满足条件的 (i, l) 对,把所有的 (i, l) 数对累加,就是我们最后要求的答案了。
3、于是问题转变成了求 找到数组下标为 0 到 j-1 的数中,小于 nums[k] 的个数 和 找到数组下标为 k+1 到 n-1 的数中,大于 nums[j] 的个数;
4、定义两个辅助数组 less[4001][4001] 和 bigger[4001][4001],令 less[i][j] 表示前 i-1 个数中,小于 j 的数的个数;令 bigger[i][j] 表示 i 以后(不包括 i)的数中,大于 j 的数的个数。less 和 bigger 的含义类似,通过两个 for 循环 枚举求出 less 和 bigger。
5、最后,只要枚举 j 和 k,在满足 nums[j] > nums[k] 的条件下,累加 less[j][ nums[k] * bigger[k][nums[j]] 的和,就是我们要求的解了。
五、题目练习
2656. K 个元素的最大和
int maximizeSum(int* nums, int numsSize, int k){
int max = 0;
for(int i = 0; i < numsSize; ++i) {
if(nums[i] > max) {
max = nums[i];
}
}
int ans = max;
while(--k) {
ans += max + 1;
max += 1;
}
return ans;
}
414. 第三大的数
#define INF -213214121
int thirdMax(int* nums, int numsSize){
// 找最大值
int max = nums[0];
for(int i = 1; i < numsSize; ++i) {
if(max < nums[i]) {
max = nums[i];
}
}
// 找第二大的数
int subMax = INF;
for(int i = 0; i < numsSize; ++i) {
if(subMax == INF) {
if(nums[i] < max) subMax = nums[i];
}else {
if(nums[i] > subMax && nums[i] < max) {
subMax = nums[i];
}
}
}
//不存在第二大的,返回第一大的
if(subMax == INF) return max;
//找第三大的数
int triMax = INF;
for(int i = 0; i < numsSize; ++i) {
if(triMax == INF) {
if(nums[i] < subMax) triMax = nums[i];
}else {
if(nums[i] > triMax && nums[i] < subMax) {
triMax = nums[i];
}
}
}
if(triMax == INF) return max;
return triMax;
}