二叉搜索树
- 二叉搜索树
- 二叉搜索树的基本概念
- 二叉搜索树的查找方法
- 二叉搜索树的代码实现
- 二叉搜索树的结点
- 二叉树的构造函数 析构函数
- 二叉排序树的插入
- 二叉树的删除
- 二叉树的拷贝构造
- 递归删除版本
- 完整代码
二叉搜索树
二叉搜索树的基本概念
二叉搜索树的特点:
- 左子树都小于根节点,右子树都大于根节点。
- 右子树都大于根节点,左子树都小于根节点。
二叉搜索树的查找方法
大于则去左侧,小于则去右侧。
二叉搜索树的代码实现
二叉搜索树的结点
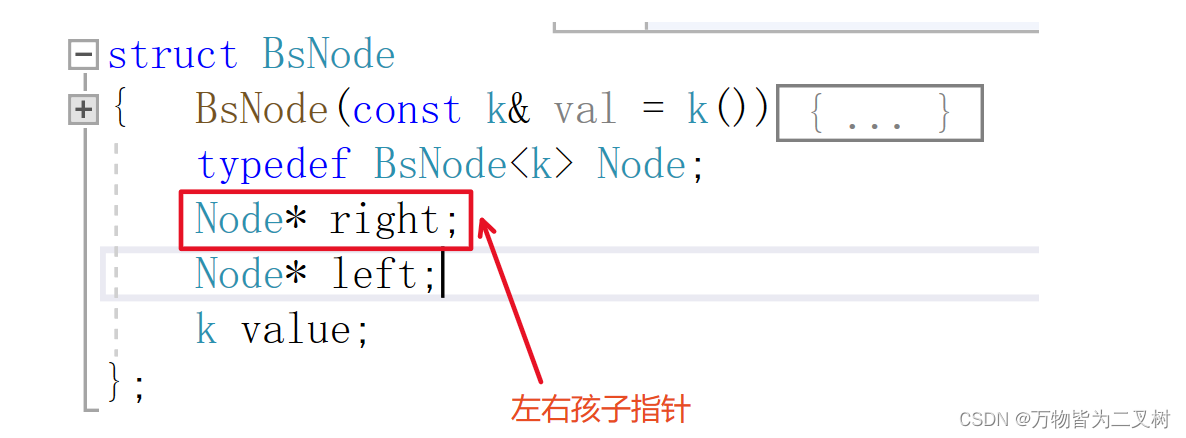
二叉树的构造函数 析构函数
二叉树的构造函数很简单,对一般二叉排序树。构造方法简单。析构函数需要重点说析构函数,析构的时候需要销毁所有的结点。然后,在释放根结点。
销毁的时候需要后序遍历销毁所有结点。
void destroy(Node* root)
{
if (root == nullptr)
{
return;
}
destroy(root->left);
destroy(root->right);
delete root;
}
后序遍历才可以,否则删除不干净。
二叉排序树的插入
二叉排序树的插入就是和二叉排序树的查找一致。二叉排序树插入时,大了就去右树,小了就去左树。
bool insert(const k& val)
{
if (_root == nullptr)//如果根为空则插入
{
_root = new Node(val);
return true;
}
Node* cur = _root;
Node* parent = cur;
while (cur)
{
if (cur->value == val)//等于则说明已经有了,插入失败
{
return false;
}
else if (cur->value < val)
{
parent = cur;
cur = cur->right;
}
else
{
parent = cur;
cur = cur->left;
}
}
cur = new Node(val);//创建新节点
if (parent->value < val)
{
parent->right = cur;
}
else
{
parent->left = cur;
}
return true;
}
二叉树的删除
删除的第一步是查找的删除的位置cur. 我们和插入一样的做法。
- 删除叶子
if (cur->right == nullptr && cur->left == nullptr)
{
if (cur == parentcur->right)
{
parentcur->right = nullptr;
}
else
{
parentcur->left = nullptr;
}
delete cur;
}
- 删除只有左子树
删除拥有左子树的结点时,将左子树接到该结点原来所在位置即可。
删除左子树为空 注意两种可能:
1 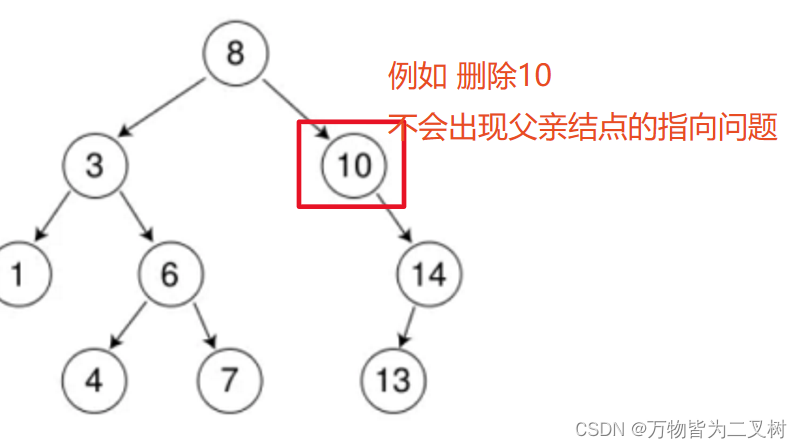
2 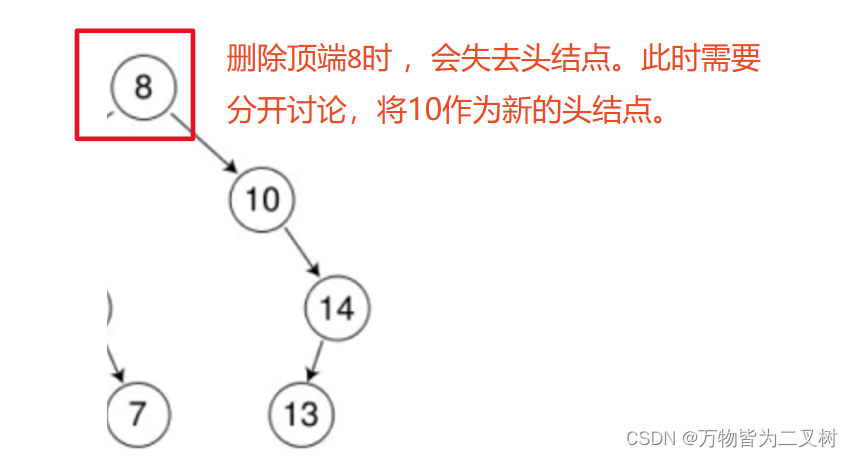
else if (cur->left == nullptr)
{
// 判断他是那个子树
//链接到父子树后面
if (cur == _root)
{
_root = cur->right;
}
else
{
if (cur == parentcur->right)
{
parentcur->right = cur->right;
}
else
{
parentcur->left = cur->right;
}
}
delete cur;
break;
}
- 删除只有右子树
删除只有右子树和删除只有左子树一样。 - 删除左右子树都有
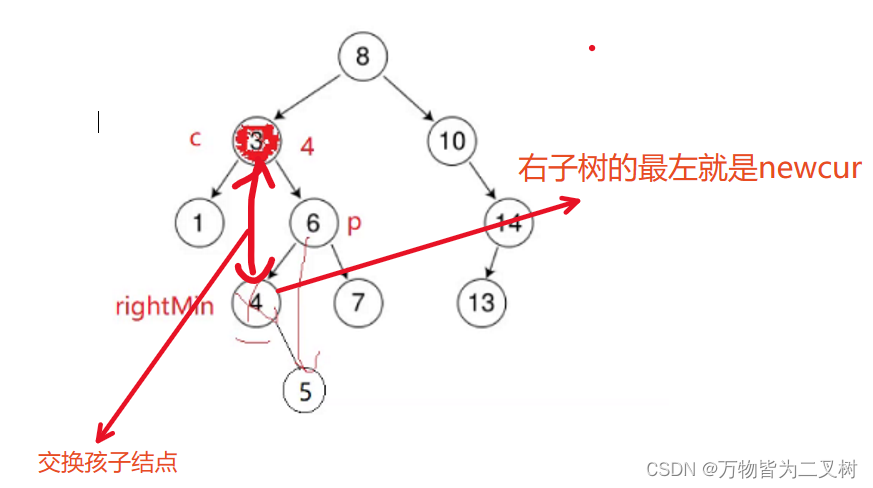
交换结点的值 然后转化成删除 只有右孩子的树。
else
{
Node* newcurfath = cur;//这里不能空 否则删除头结点会报错。
Node* newcur = nullptr;
newcur = cur->right;
while (newcur->left)//找可以替换的子结点
{
newcur = newcur->left;
}
cur->value = newcur->value;//交换结点
if (newcur == newcurfath->right)
{
newcurfath->right = newcur->right;
}
else
{
newcurfath->left = newcur->right;
}
delete newcur;
}
二叉树的拷贝构造
二叉树的拷贝构造是需要通过递归,也就是前序遍历。边前序遍历边开辟空间拷贝构造。
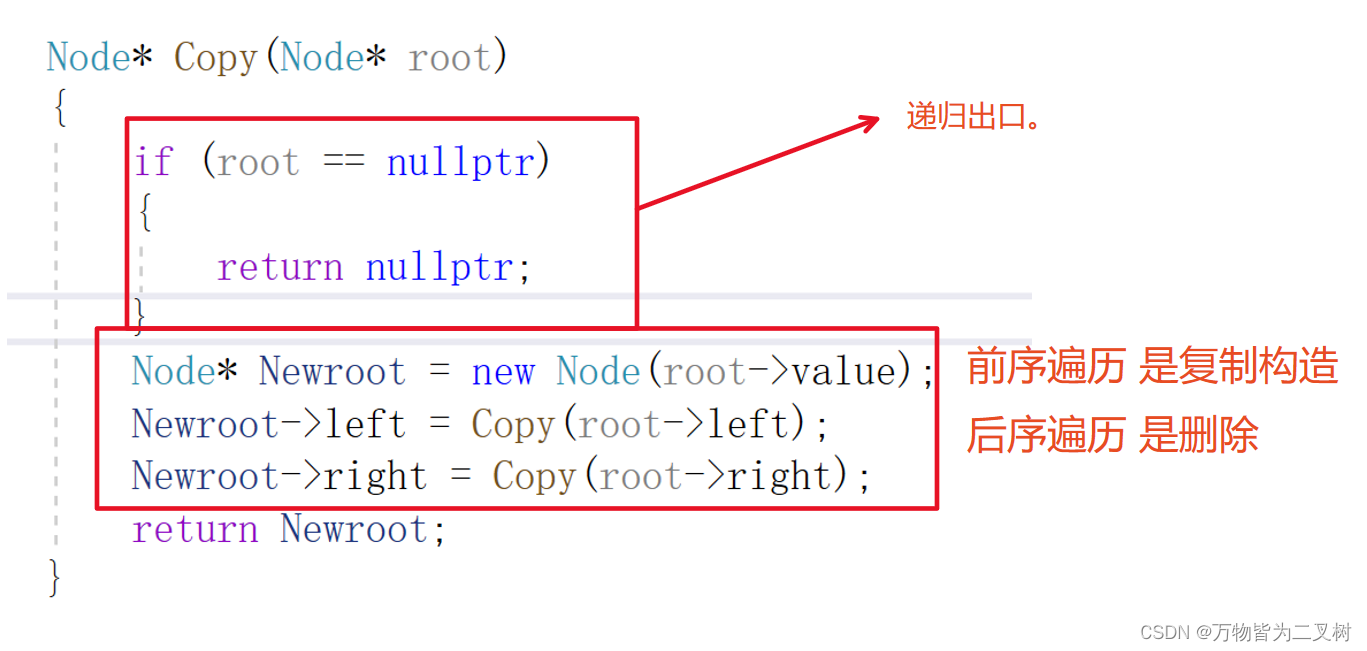
最后 拷贝构造的经典问题,传引用 不能传指针。
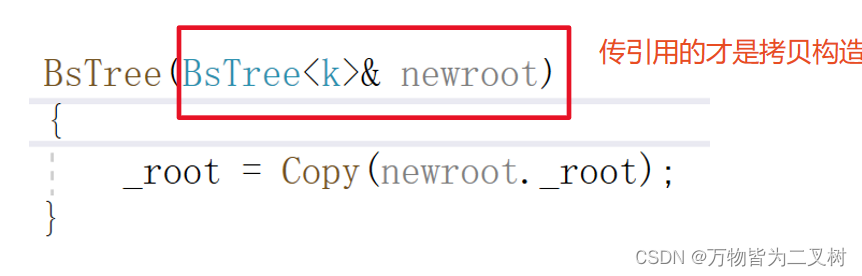
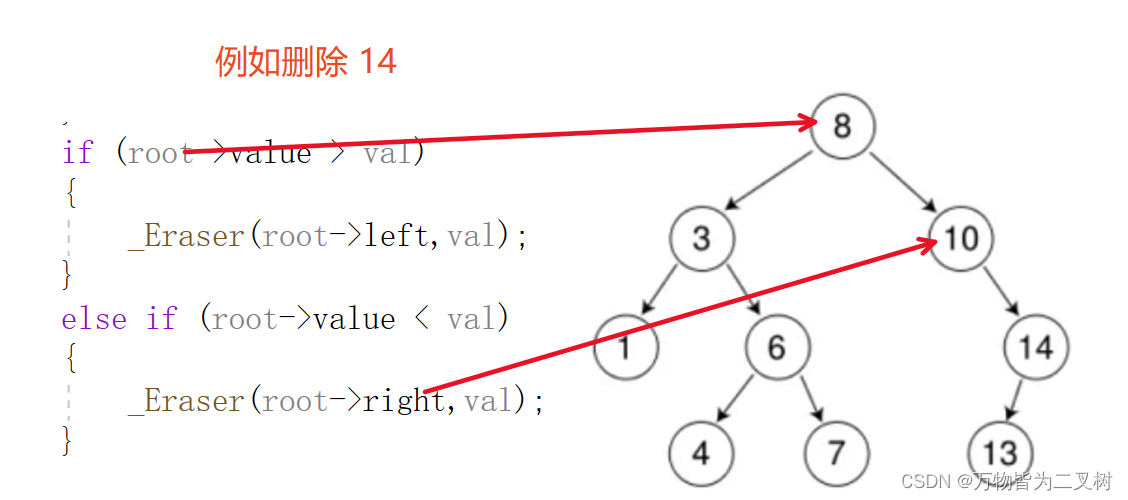
递归删除版本
递归是借助引用。每递归一次,进入一颗子树。恰好引用的就是当前的头结点。


完整代码
#pragma once
#include<iostream>
#include<string>
using namespace std;
template <class k>
struct BsNode
{ BsNode(const k& val = k())
:right (nullptr)
, left (nullptr)
, value (val)
{
}
typedef BsNode<k> Node;
Node* right;
Node* left;
k value;
};
template <class k>
class BsTree
{
typedef BsNode<k> Node;
public:
BsTree()
:_root(nullptr)
{
}
BsTree(BsTree<k>& newroot)
{
_root = Copy(newroot._root);
}
bool insert(const k& val)
{
if (_root == nullptr)//如果根为空则插入
{
_root = new Node(val);
return true;
}
Node* cur = _root;
Node* parent = cur;
while (cur)
{
if (cur->value == val)//等于则说明已经有了,插入失败
{
return false;
}
else if (cur->value < val)
{
parent = cur;
cur = cur->right;
}
else
{
parent = cur;
cur = cur->left;
}
}
cur = new Node(val);//创建新节点
if (parent->value < val)
{
parent->right = cur;
}
else
{
parent->left = cur;
}
return true;
}
bool find(const k& val)
{
Node* cur = _root;
while (cur)
{
if (cur->value == val)
{
return true;
}
else if (cur->value>val)
{
cur = cur->right;
}
else
{
cur = cur->left;
}
}
return false;
}
bool Erase(const k& val)
{
Node* cur = _root;
Node* parentcur = _root;
while (cur)
{
if (cur->value == val)
{
if (cur->right == nullptr && cur->left == nullptr)
{
if (cur == parentcur->right)
{
parentcur->right = nullptr;
}
else
{
parentcur->left = nullptr;
}
delete cur;
break;
}
else if (cur->right == nullptr)
{
if (cur == _root)
{
_root = cur->left;
}
else
{
if (cur == parentcur->right)
{
parentcur->right = cur->left;
}
else
{
parentcur->left = cur->left;
}
}
delete cur;
break;
}
else if (cur->left == nullptr)
{
// 判断他是那个子树
//链接到父子树后面
if (cur == _root)
{
_root = cur->right;
}
else
{
if (cur == parentcur->right)
{
parentcur->right = cur->right;
}
else
{
parentcur->left = cur->right;
}
}
delete cur;
break;
}
else
{
Node* newcurfath = cur;
Node* newcur = nullptr;
newcur = cur->right;
while (newcur->left)
{
newcur = newcur->left;
}
cur->value = newcur->value;
if (newcur == newcurfath->right)
{
newcurfath->right = newcur->right;
}
else
{
newcurfath->left = newcur->right;
}
delete newcur;
}
}
else if (cur->value > val)
{
parentcur = cur;
cur = cur->left;
}
else
{
parentcur = cur;
cur = cur->right;
}
}
return true;
}
void print()
{
inorder(_root);
cout << endl;
}
bool Eraser(const k& val)
{
return _Eraser(_root, val);
}
~BsTree()
{
destroy(_root);
_root = nullptr;
}
private:
bool _Eraser(Node* &root, const k& val)
{
if (root == nullptr)
{
return false;
}
if (root->value > val)
{
_Eraser(root->left,val);
}
else if (root->value < val)
{
_Eraser(root->right,val);
}
else
{
Node* tmp = root;
if (root->left == nullptr)
{
root = root->right;
}
else if (root->right == nullptr)
{
root = root->left;
}
else
{
Node* newcur = nullptr;
newcur = root->right;
while (newcur->left)
{
newcur = newcur->left;
}
swap(newcur->value,_root->value);
return _Eraser(root->right, val);
}
delete tmp;
return true;
}
}
void destroy(Node* root)
{
if (root == nullptr)
{
return;
}
destroy(root->left);
destroy(root->right);
delete root;
}
void inorder(Node* root)
{
if (root == nullptr)
{
return;
}
inorder(root->left);
cout << root->value << ' ';
inorder(root->right);
}
Node* Copy(Node* root)
{
if (root == nullptr)
{
return nullptr;
}
Node* Newroot = new Node(root->value);
Newroot->left = Copy(root->left);
Newroot->right = Copy(root->right);
return Newroot;
}
Node* _root;
};