语言:Java/Go
理论
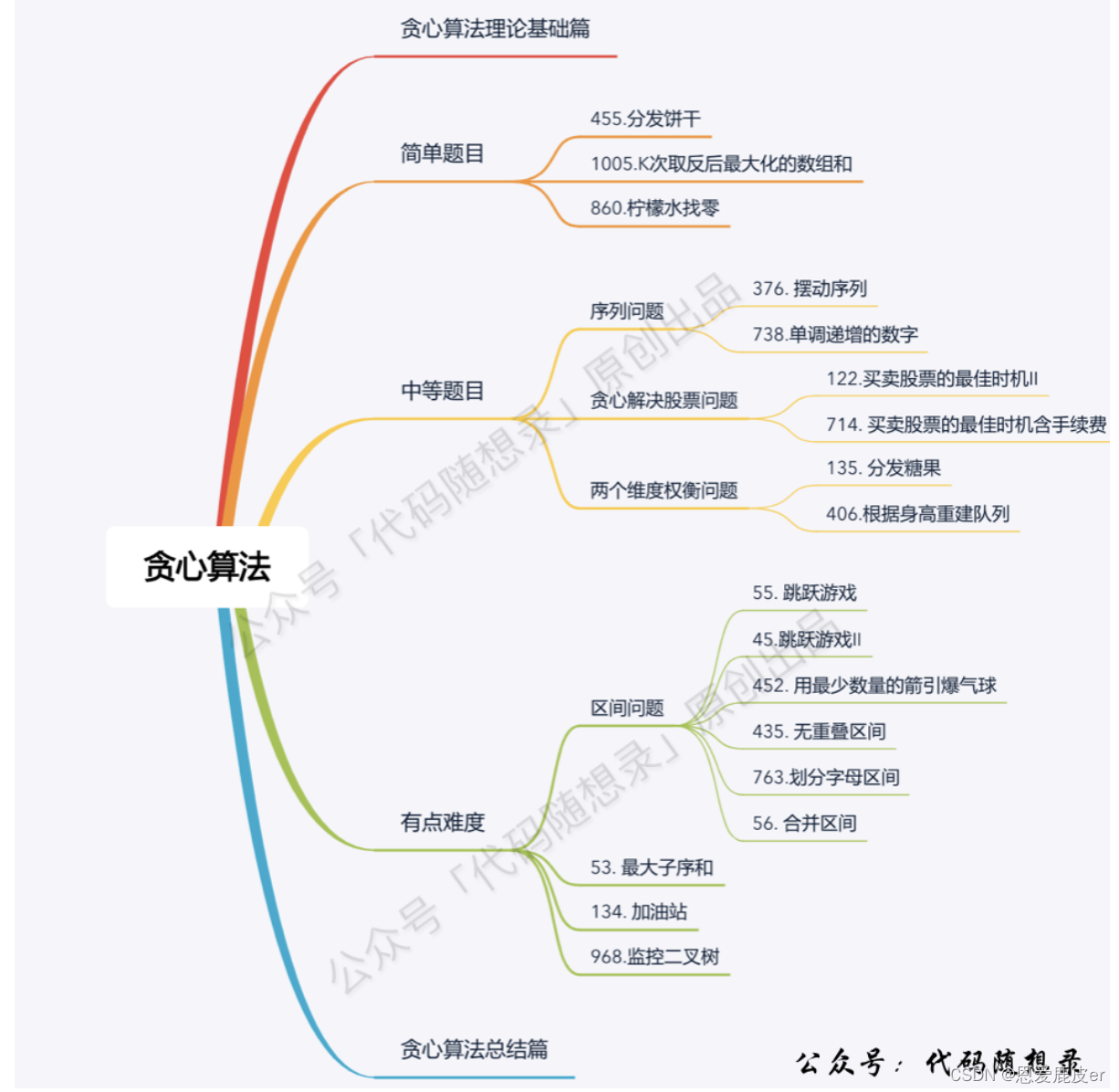
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
什么时候用贪心?可以用局部最优退出全局最优,并且想不到反例到情况
贪心的一般解题步骤
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
455.分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
- 输入: g = [1,2,3], s = [1,1]
- 输出: 1 解释:你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1,2,3。虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。所以你应该输出 1。
示例 2:
- 输入: g = [1,2], s = [1,2,3]
- 输出: 2
- 解释:你有两个孩子和三块小饼干,2 个孩子的胃口值分别是 1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2.
本题的目标是满足更多孩子的胃口,因此大的饼干就优先满足胃口大的孩子,才会确保没有资源浪费。因此局部最优解就是将一定尺寸的饼干尽量喂给与这个尺寸接近胃口的孩子。全局最优就是喂饱尽可能多的孩子。可以先将饼干和胃口数组进行排序,从后向前遍历孩子数组,将大饼干给胃口大的孩子,并且设置一个count统计满足小孩的数量。
class Solution {
public int findContentChildren(int[] g, int[] s) {
//先对两个数组进行排序
Arrays.sort(g);
Arrays.sort(s);
int count=0;
int index=s.length-1; //饼干数组的下标
for(int i=g.length-1;i>=0;i--){//先遍历胃口
if(index>=0 && g[i]<=s[index]){ //再去查找饼干
count++;
index--; //满足条件才会把饼干分配出去,饼干的指针也往前移动
}
}
return count;
}
}⚠️注意:如果是从后向前遍历,应该先遍历胃口再遍历饼干,因为这样才不会出现饼干没有合理分配的情况。如果是用小饼干喂饱小胃口,则需要先遍历饼干,再遍历胃口。
376. 摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
- 输入: [1,7,4,9,2,5]
- 输出: 6
- 解释: 整个序列均为摆动序列。
示例 2:
- 输入: [1,17,5,10,13,15,10,5,16,8]
- 输出: 7
- 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
本题目的是通过删除某些元素,找到最长的摆动子序列并返回其长度。摆动序列如果在一个坐标轴上描点,应该是持续存在n个峰值的序列。如下图:

可以看出需要删除的节点应该是,单调递增/递减时,非端点的节点。此时一个坡度上会有两个局部峰值。全局最优就是找到局部峰值最多的序列。因为本题返回最长子序列的长度,所以不需要进行删除操作,只需要统计局部峰值的个数即可。
计算当前节点和前后节点的关系:prediff(nums[i] - nums[i-1])和curdiff(nums[i+1] - nums[i])
若prediff < 0 && curdiff > 0或者prediff > 0 && curdiff < 0,满足这两个条件的时候,说明nums[i-1],nums[i],nums[i+1]均为峰值。- 若遇到平坡,假设上坡后平坡:即prediff > 0 && curdiff = 0,遇到最后一个平坡节点时候,应该是这样的条件:prediff = 0 && curdiff < 0,将这个节点保留,其他平坡的节点都删除。所以当前峰值的条件为(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)第一个情况就是下坡,第二个情况为上坡。
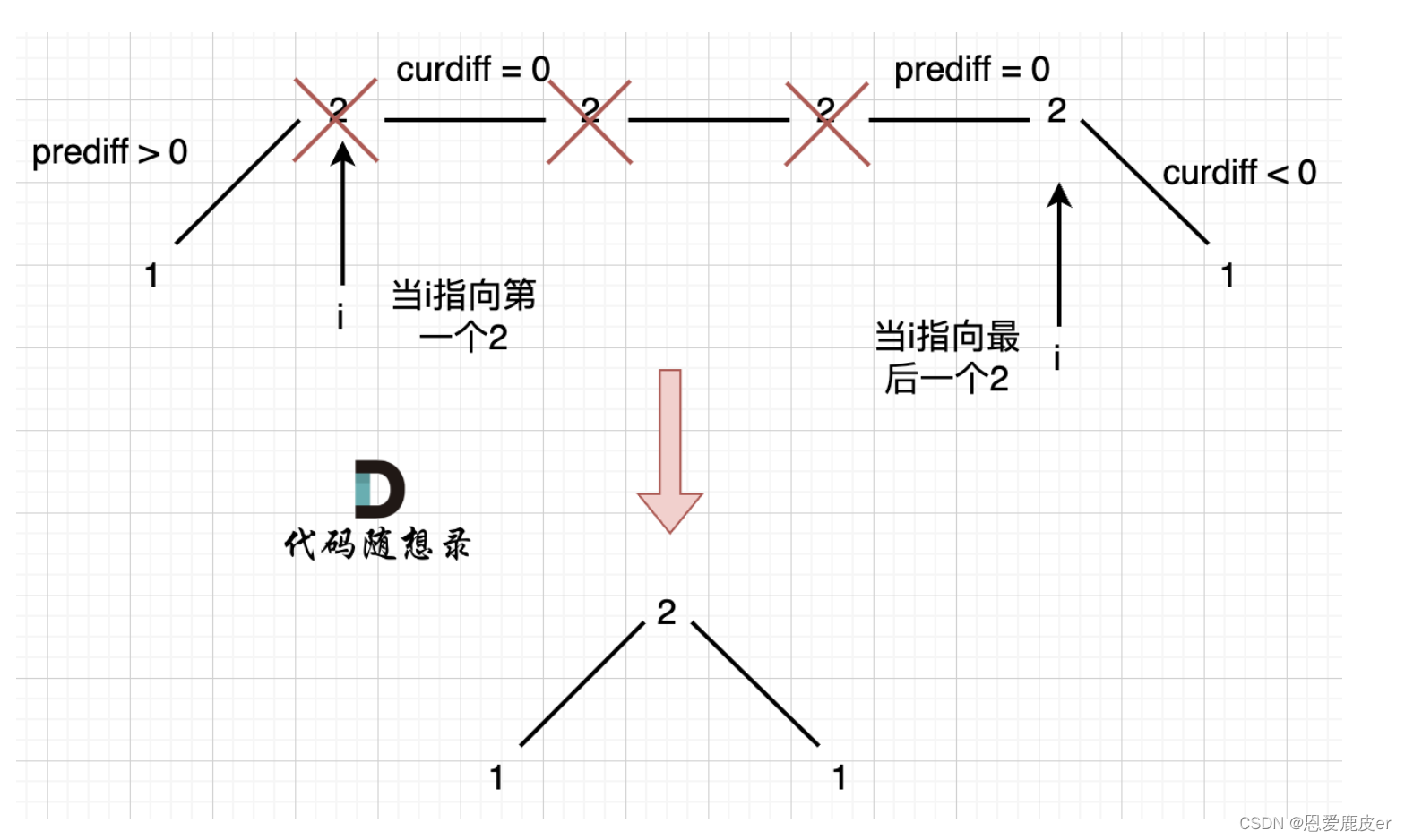
- 若遇到单调坡度有平坡,我们只需要在 这个坡度 摆动变化的时候,更新 prediff 就行,这样 prediff 在 单调区间有平坡的时候 就不会发生变化,造成误判。
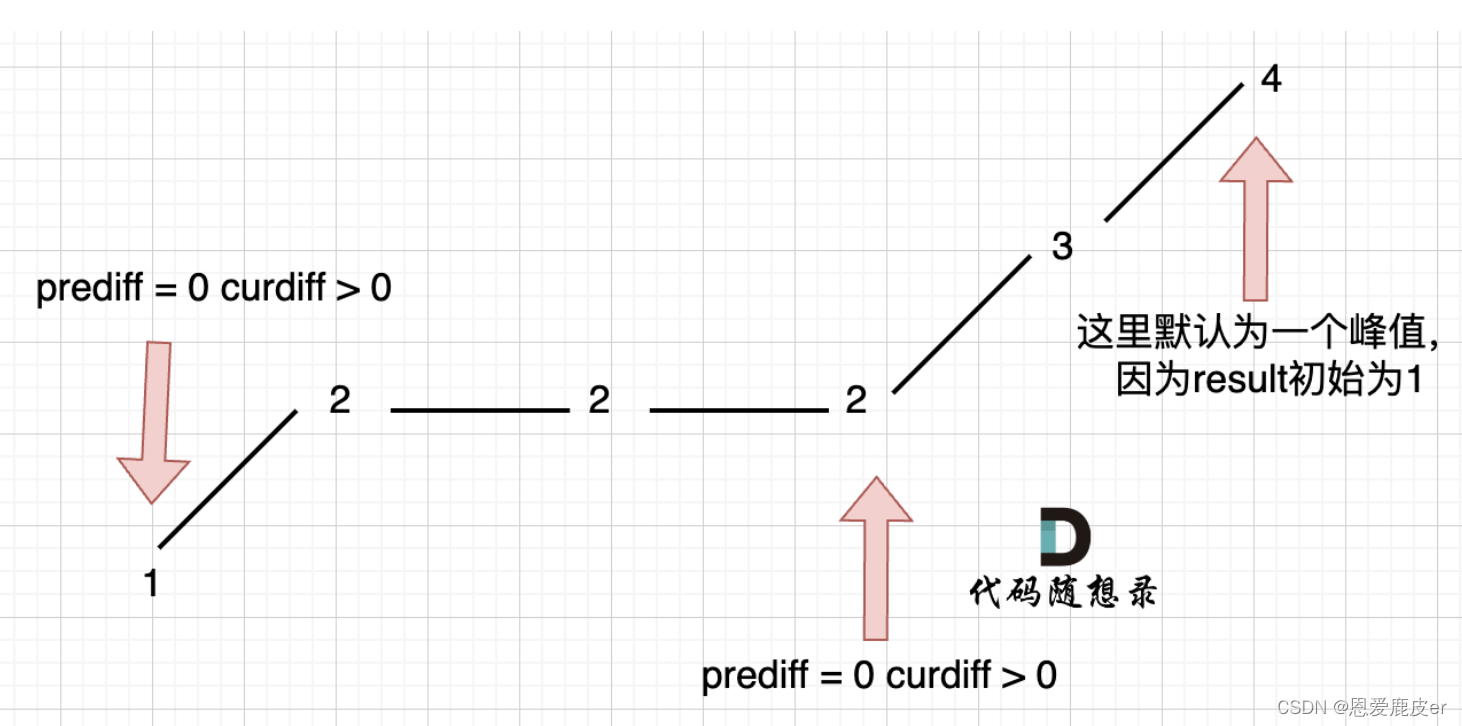
数组首尾两端:题目中说了,如果只有两个不同的元素,那摆动序列也是 2。例如序列[2,5],如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。因为我们在计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i])的时候,至少需要三个数字才能计算,而数组只有两个数字。这里我们可以写死,就是 如果只有两个元素,且元素不同,那么结果为 2。也可以不写死,假设数组最前面还有一个数字,那这个数字应该是什么呢?之前我们在 讨论 情况一:相同数字连续 的时候, prediff = 0 ,curdiff < 0 或者 >0 也记为波谷。那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0
class Solution {
public int wiggleMaxLength(int[] nums) {
if(nums.length<=1) return nums.length;
int curDiff=0; //记录当前节点和后一个节点的差值
int preDiff=0; //记录前一个节点和当前节点的差值
int result=1;
for(int i=0;i<nums.length-1;i++){
curDiff=nums[i+1]-nums[i];
if(preDiff<=0&&curDiff>0 || preDiff>=0 && curDiff<0){//出现峰谷的时候
result++;
preDiff=curDiff;
}
}
return result;
}
}53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
- 输入: [-2,1,-3,4,-1,2,1,-5,4]
- 输出: 6
- 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
本题跟上题的区别在于,要求连续。因此不可以进行删除也不可以对数组重排序。本题的直接思路就是两层for循环嵌套,但是时间复杂度太高。可以考虑用贪心算法或动态规划算法。
先尝试找局部最优:比如看前两个元素:-2,1,肯定会先以1作为开头,把1加入到结果中,在sum上加上1,任何负值只会减少和的值。当以1为开头时,又遇到了-3,这时sum变成了负值,所以将1从结果中删除,从3点后面一个元素开始判断,以此类推。还要设置变量maxSum记录最大的和。因此,如果当加上nums[i]时sum变为负数时,就将sum变为0重新计算。
class Solution {
public int maxSubArray(int[] nums) {
if(nums.length==1) return nums[0];
int sum=0;
int maxSum=Integer.MIN_VALUE;
for(int i=0;i<nums.length;i++){
sum+=nums[i];
maxSum=Math.max(sum, maxSum);
if(sum<=0) sum=0;
}
return maxSum;
}
}