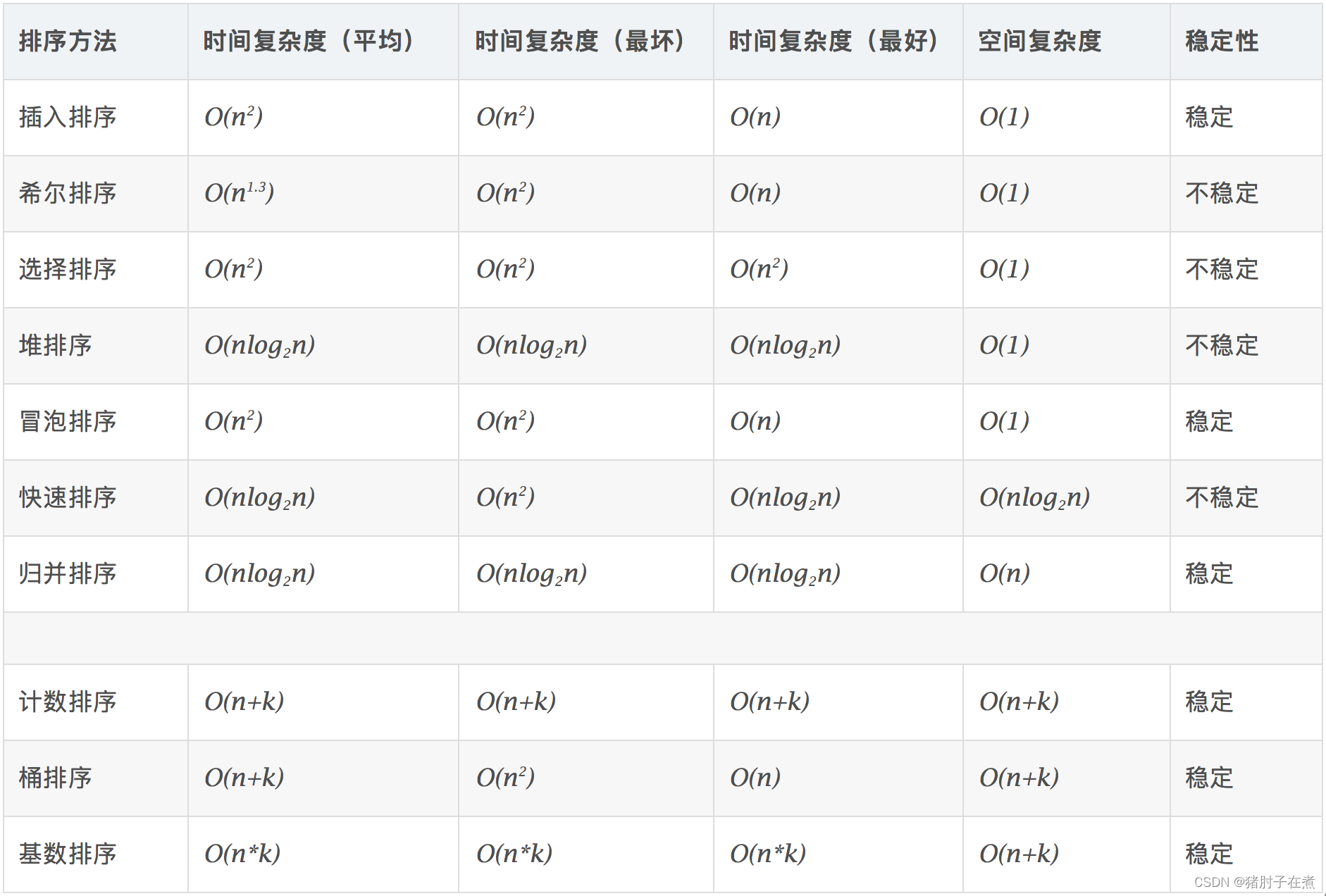
排序算法总结

直接插入排序

取出未排序部分的第一个元素，与已排序的部分从后往前比较，找到合适的位置。将大于它的已排序的元素向后移动，将该元素插入到合适的位置。

//1. 直接插入排序
void InsertionSort(vector<int>& nums){
    for(int i=1;i<nums.size();i++){
        int key = nums[i];//取出未排序部分的第一个元素
        int j =i-1;
        // 将这个元素与已排序部分的元素从后向前比较，找到合适的位置插入
        while(j>=0 && nums[j]>key){
            nums[j+1]=nums[j];// 已排序的元素向后移动
            j--;
        }
        nums[j+1]=key; // 插入到正确位置
    }
}

希尔排序

希尔排序是一种基于插入排序的算法，通过引入间隔序列来允许交换距离较远的元素，从而对数组进行部分排序，这个过程重复进行，每次都减小间隔，直到整个数组被排序。

//2. 希尔排序,分组后组内进行直接插入排序
void shellSort(vector<int>& nums){
    int n = nums.size();
    //gap最初为n/2，然后不断减小直至为1
    for(int gap = n/2; gap>0 ;gap/=2){
        for(int i = gap ;i < n; i += 1){
            //获取未排序的第一个元素
            int key = nums[i];
            int j=i-gap;
            //前一个元素是i-gap;
            while(j>=0 && nums[j]>key){
                nums[j+gap]=nums[j];
                j-=gap;
            }
            nums[j+gap]=key;
        }
    }
}

冒泡排序

冒泡排序的核心思想是通过重复遍历要排序的列表，比较每对相邻的项，然后交换它们（如果它们是在错误的顺序）。这个过程重复进行，直到没有需要交换的项，这意味着列表已经排序完成。每完成一轮遍历，至少一个元素会被移动到其最终位置。

//3. 冒泡排序
void bubbleSort(vector<int>& nums){
    int n = nums.size();
    for(int i=0;i<n-1;i++){   
        bool flag = false;
        for(int j=0;j<n-i-1;j++){
            if(nums[j]>nums[j+1])
                swap(nums[j],nums[j+1]);
            flag = true;
        }
        if(flag==false) return; //如果这一趟没有发生任何交换，则意味已经有序。
    }
}

快速排序

快速排序是一种高效的排序算法，采用分治法的思想来对数组进行排序。它的基本步骤是选择一个元素作为基准（pivot），重新排列数组，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准的后面（相等的数可以到任一边）。在这个分区退出之后，该基准就处于数组的中间位置。这个过程称为分区（partition）操作。然后，递归地（recursive）把小于基准值元素的子数组和大于基准值元素的子数组排序。

//4. 快速排序
int partition(vector<int>& nums,int low, int high)
{
    int pivot=nums[low];
    int i=low;
    int j=high;
    while(i<j){
        // 从右向左找到第一个小于等于pivot的数   
        while(i<j && nums[j]>pivot){
            j--;
        }
        if(i<j){
            nums[i]=nums[j];
            i++;
        }
        // 从左向右找到第一个大于pivot的数
        while(i<j && nums[i]<pivot){
            i++;
        }
        if(i<j){
            nums[j]=nums[i];
            j--;
        }
    }
    nums[i]=pivot;// 将基准值放到正确的位置
    return i; // 返回基准值的位置
}

void quickSort(vector<int>& nums, int low, int high){
    if(low<high){
        // pi是partitioning index，arr[pi]现在在正确的位置
        int pi = partition(nums,low,high);// 分区操作，并返回基准值的索引
        quickSort(nums,low,pi-1);//对左子树进行快速排序
        quickSort(nums,pi+1,high);//对右子树进行快速排序
    }
        
}

简单选择排序

简单选择排序是一种直观且基础的排序算法。它的工作原理是：遍历数组，每次从未排序的部分选出最小（或最大）的元素，放到已排序部分的末尾。这个过程重复进行，直到整个数组排序完成。简单选择排序的时间复杂度为O(n^2)，在任何情况下都是这样，这使得它在处理大数据集时不够高效。然而，由于其实现简单，它在数据量不大时仍然是一个不错的选择。

// 5. 简单选择排序：找到最小的元素后，和第一个元素交换
void simpleSort(vector<int>& nums)
{
    for(int i=0;i<nums.size();i++){
        // 寻找[i, n)区间里的最小值的索引
        int minindex=i;
        for(int j=0;i<nums.size();j++)
        {
            if(nums[j]<nums[minindex]){
                minindex=j;
            }
        }
        swap(nums[i],nums[minindex]);
    }
}

堆排序

小根堆的时候是降序排列，大根堆是升序排列。

// 调整根堆，i是要调整的节点索引，n是堆的大小
void heapify(vector<int>& nums, int n, int i) {
    int smallest = i; // 初始化最小元素为当前节点
    int left = 2 * i + 1; // 左子节点
    int right = 2 * i + 2; // 右子节点

    // 如果左子节点更小，则更新最小元素的索引
    if (left < n && nums[left] < nums[smallest]) {
        smallest = left;
    }
    // 如果右子节点更小，则更新最小元素的索引
    if (right < n && nums[right] < nums[smallest]) {
        smallest = right;
    }
    // 如果最小元素不是当前节点，交换它们，并对交换后的节点进行调整
    if (smallest != i) {
        swap(nums[i], nums[smallest]);
        heapify(nums, n, smallest);
    }
}

// 堆排序
void heapSort(vector<int>& nums) {
    int n = nums.size();
    //构建小根堆（从最后一个非叶子节点往上，最后一个非叶子节点是n/2-1)
    for(int i = n/2-1;i>=0;i--)
    {
        heapify(nums,n,i);
    }
    //一个个从小根堆中取出，然后调整堆
    for(int i=n-1;i>0;i--){
        swap(nums[0],nums[i]);
        heapify(nums,i,0);
    }
}

归并排序

// 7. 归并排序
// 归并两个子数组的函数
// 第一个子数组是 arr[l..m]
// 第二个子数组是 arr[m+1..r]
// 归并排序是一种高效的排序算法，采用分治法的一个应用。
// 它将数组分成两半，对每部分递归地应用归并排序，
// 然后将两部分合并成一个有序数组。
// 这个过程包括分解数组成为越来越小的部分，
// 直至每个小部分只有一个元素，然后开始合并这些小部分，
// 使之有序，最终得到完全排序的数组。
void merge(vector<int>& nums,int l,int m,int r){
    int i,j,k;
    int n1=m-l+1;//左边的大小
    int n2=r-m;//右边的大小
    // 创建临时数组
    vector<int> L(n1),R(n2);
    // 拷贝数据到临时数组L R
    for(int i=0;i<n1;i++)
        L[i]=nums[l+i];
    for (j = 0; j < n2; j++)
        R[j] = nums[m + 1 + j];
    
    //归并临时数组到nums[l-r]
    i=0;
    j=0;
    k=l;
    while(i<n1 && j<n2){
        if (L[i] <= R[j]) {
            nums[k] = L[i];
            i++;
        } else {
            nums[k] = R[j];
            j++;
        }
        k++;
    }
    // 拷贝 L[] 的剩余元素
    while (i < n1) {
        nums[k] = L[i];
        i++;
        k++;
    }

    // 拷贝 R[] 的剩余元素
    while (j < n2) {
        nums[k] = R[j];
        j++;
        k++;
    }

}
void mergeSort(vector<int>& nums, int l, int r)
{   
    if(l<r){
        int m=l+(r-l)/2;

        //分别对左右办部分进行排序
        mergeSort(nums,l,m);
        mergeSort(nums,m+1,r);

        //合并这两个部分
        merge(nums,l,m,r);

    }

}

reference

https://leetcode.cn/circle/discuss/rzsN73/ 排序算法大汇总
https://mp.weixin.qq.com/s/FFsvWXiaZK96PtUg-mmtEw TOPk问题大汇总