LeetCode 热题 HOT 100(P1~P10)

🔥 LeetCode 热题 HOT 100

这里记录下刷题过程中的心得，其实算法题基本就是个套路问题，很多时候你不知道套路或者模板，第一次尝试去做的时候就会非常懵逼、沮丧和无助。而且就算你一时理解并掌握了，过一段时间往往会绝望的发现你又不会了。所以过遍数就非常重要，我目前配合 anki 来复习。

LC001two_sum 两数之和（简单）

. - 力扣（LeetCode）

题目：

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那两个整数，并返回它们的数组下标。

解法：

使用HashMap 是比较常规的解法，这里有个技巧是只通过一遍循环就能解决问题。从头开始遍历，然后顺便把元素放入HashMap，这样就不用先遍历一遍初始化HashMap。

public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> cache = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int value = target - nums[i];
            if (cache.containsKey(value)) {
                return new int[]{ i, cache.get(value) };
            }
            cache.put(nums[i], i);
        }
        return null;

    }

LC002add_two_numbers 两数相加（中等）

题目：

给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

解法：

链表题通常的操作是先增加一个前置pre 节点，这样就能大大方便后续的操作。因为最后你要返回头节点，这个时候pre.next 就是。

这道题核心难点是对进位的处理，因此需要有一个变量表示每次的进位，同时在最后还要对进位进行判断，这点特别容易遗漏。剩下的就是一些细节的处理，有一些为null 的情况需要处理，这点也非常容易踩坑。

 public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode pre = new ListNode(0);
        ListNode cur = pre;
        //表示进位
        int carry = 0;
        while (l1 != null || l2 != null) {
            int left = l1 == null ? 0 : l1.val;
            int right = l2 == null ? 0 : l2.val;

            int sum = left + right + carry;
            carry = sum / 10;
            sum = sum % 10;
            cur.next = new ListNode(sum);
            cur = cur.next;

            l1 = l1 == null ? null : l1.next;
            l2 = l2 == null ? null : l2.next;
        }
        if (carry == 1) {
            cur.next = new ListNode(carry);
        }
        return pre.next;
    }

LC003longest_substring 无重复字符的最长子串（中等）

. - 力扣（LeetCode）

题目：

给定一个字符串 s ，请你找出其中不含有重复字符的最长子串的长度

解法：

典型的滑动窗口策略，窗口的左右下标刚开始都是0，首先需要一个缓存用于存放已经遍历过的字符。右下标开始遍历，并跟缓存中的字符比较，存在就说明遇到重复的了，这个时候左右下标构成的字符串就是非重复的字符串，然后当前元素进缓存，左下标往前。这里需要注意要设置一个起始点，在每次判断更新最大长度的时候需要记录下这个起始点下标，不然最后输出的时候没办法定位。

public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> cache = new HashMap<>();
        int left = 0, max = 0;
        for (int i = 0; i < s.length(); i++) {
            final char key = s.charAt(i);
            if (cache.containsKey(key)) {
                // 这里+1 说明遇到重复字母，left 标往前挪动了一位
                left = Math.max(left, cache.get(key) + 1);
            }
            cache.put(key, i);
            max = Math.max(max, i - left + 1);
        }
        return max;
    }

这里有个优化性能的小技巧，因为字符由由英文字母、数字、符号和空格组成，因此可以用asc2 表示，这样可以用int[128] 代替HashMap。

LC004median_of_two 寻找两个正序数组的中位数（困难）

. - 力扣（LeetCode）

题目：

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。

算法的时间复杂度应该为 O(log (m+n)) 。

解法：

难点在于复杂度要求为log，这个典型折半查找的思路了。

根据中位数的定义，当 m+n是奇数时，中位数是两个有序数组中的第 (m+n)/2 个元素，当 m+n 是偶数时，中位数是两个有序数组中的第 (m+n)/2 个元素和第 (m+n)/2+1 个元素的平均值。因此，这道题可以转化成寻找两个有序数组中的第 k 小的数，其中 k 为 (m+n)/2 或 (m+n)/2+1。

剩下的问题就是怎么在两个数组中找第k个数，并且还要是log 的复杂度。这里直接给结论，先比较两个数组中k/2 位置的2个数，小的那一个所在数组前k/2 就可以舍弃了，同样的思路接着找剩下的k/2，当然这里有很多细节和边界需要考虑。

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length1 = nums1.length, length2 = nums2.length;
        int totalLength = length1 + length2;
        //个数为奇数的情况
        if (totalLength % 2 == 1) {
            int midIndex = totalLength / 2;
            double median = getKthElement(nums1, nums2, midIndex + 1);
            return median;
        } else {
            //个数偶数的情况
            int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;
            double median =
                    (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;
            return median;
        }
    }

    /**
     * 注意这里的k是第k位，并不是下标k
     *
     * @param nums1
     * @param nums2
     * @param k
     * @return
     */
    public int getKthElement(int[] nums1, int[] nums2, int k) {
        /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
         * 这里的 "/" 表示整除
         * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
         * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
         * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
         * 这样 pivot 本身最大也只能是第 k-1 小的元素
         * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
         * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
         * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
         */

        int length1 = nums1.length, length2 = nums2.length;
        int index1 = 0, index2 = 0;

        while (true) {
            // 边界情况
            if (index1 == length1) {
                return nums2[index2 + k - 1];
            }
            if (index2 == length2) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {
                return Math.min(nums1[index1], nums2[index2]);
            }

            // 正常情况
            int half = k / 2;
            int newIndex1 = Math.min(index1 + half, length1) - 1;
            int newIndex2 = Math.min(index2 + half, length2) - 1;
            int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];
            if (pivot1 <= pivot2) {
                k -= (newIndex1 - index1 + 1);
                index1 = newIndex1 + 1;
            } else {
                k -= (newIndex2 - index2 + 1);
                index2 = newIndex2 + 1;
            }
        }
    }

getKthElement 可以用递归的方法改写下，这样能精简不少。

LC005longest_palindromic 最长回文子串（中等）

. - 力扣（LeetCode）

题目：

给你一个字符串 s，找到 s 中最长的回文子串。如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

解法：

这里用了动态规划，动态规划的难点在于动态方程的推导，动态方程很多时候又取决于动态数组的定义，只能说多接触不同类型的题目来增长这方面的经验。

针对这道题定义了boolean 类型的2维数组，dp[i][j] 表示s[i][j]是否为回文。

然后就是2层循环不断推进的过程。

public String longestPalindrome(String s) {
        final int len = s.length();
        if (len < 2) {
            return s;
        }
        int begin = 0, max = 1;

        //dp[i][j] 表示s[i][j]是否为回文
        boolean[][] dp = new boolean[len][len];
        final char[] charArray = s.toCharArray();
        for (int j = 0; j < len; j++) {
            for (int i = 0; i <= j; i++) {
                if (charArray[j] == charArray[i]) {
                    //只有3个的时候，只要两边相等就是回文
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        //大于3个的时候就要看进一步的情况
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }
                //如果是回文就看下是否当前最大
                if (dp[i][j] && j - i + 1 > max) {
                    begin = i;
                    max = j - i + 1;
                }
            }
        }
        return s.substring(begin, begin + max);
    }

理解了核心思想之后，其实就是一些套路了。

LC011container_with 盛最多水的容器（中等）

. - 力扣（LeetCode）

题目：

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

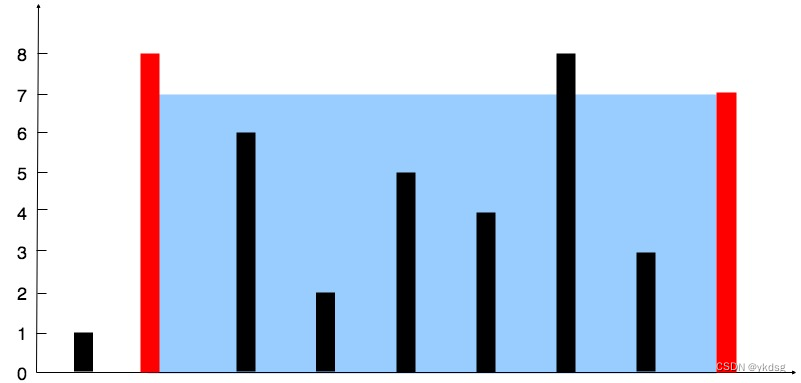
解法：

套路题，用双指针左右夹逼法求解。一开始左右指针在两边头尾，这个时候宽度是最大的，高是两边最矮的那个，然后进一步从矮的那边往中间靠近。

public int maxArea(int[] height) {
        int left = 0, right = height.length - 1;
        int max = 0;

        while (left < right) {
            int high = Math.min(height[left], height[right]);
            int wide = right - left;
            max = Math.max(max, high * wide);
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        return max;
    }

未完待续