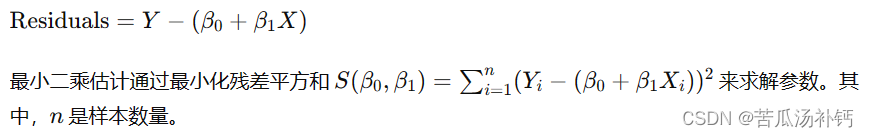[SS]语义分割_膨胀卷积

news2024/11/25 2:25:44

膨胀卷积

一、概念

1、定义

2、知识点

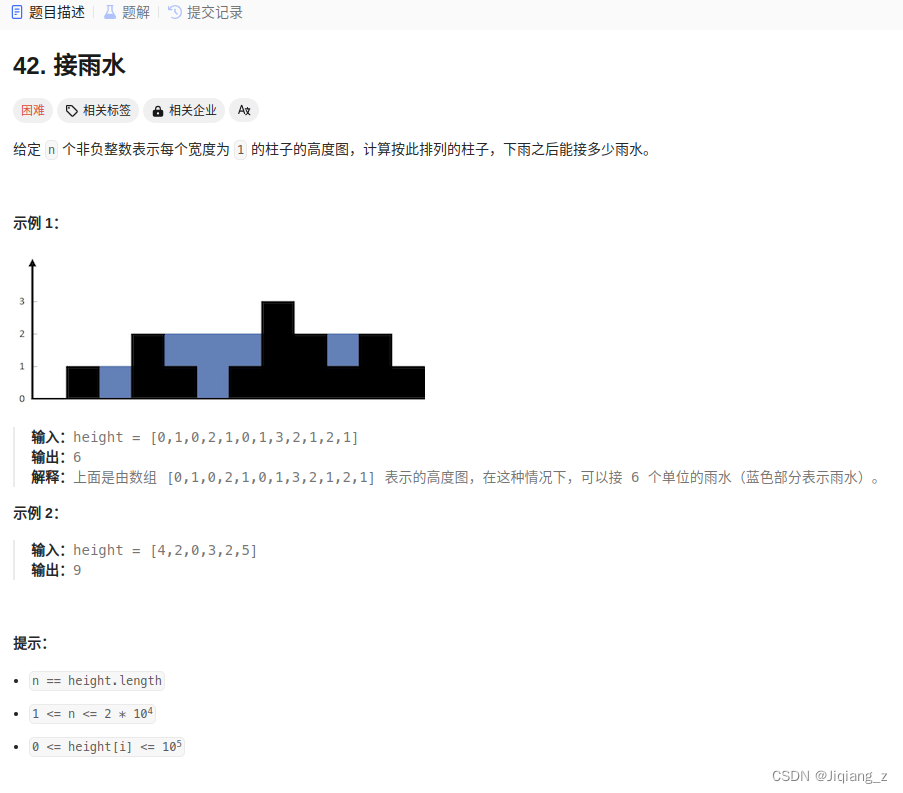
二、详细介绍

1、引入

2、膨胀系数设定

一、概念

1、定义

膨胀卷积（Dilated Convolution），也称为空洞卷积（Atrous Convolution），是一种在卷积神经网络中常用的操作。它通过在卷积核的周围插入一定数量的零值来改变卷积核的感受野大小。

传统的卷积操作是在输入特征图上滑动卷积核，每次将卷积核中的权重与输入特征图的对应位置进行相乘并求和，从而得到输出特征图中的一个像素值。膨胀卷积则是在滑动卷积核时，通过在卷积核的元素之间插入一定数量的零值来扩大感受野，使得每个卷积核的有效感受野增大。

膨胀卷积的主要优点是能够在不增加网络参数和计算量的情况下，增加网络的感受野。这对于处理具有大尺度空间信息的任务非常有用，比如目标检测和语义分割等任务。膨胀卷积可以通过增加膨胀系数来控制感受野的大小，较小的膨胀系数对应较小的感受野，较大的膨胀系数对应较大的感受野。

膨胀卷积在深度学习中的应用很广泛。比如，在语义分割任务中，可以使用膨胀卷积来扩大网络对于像素间上下文的感受能力；在图像增强任务中，可以使用膨胀卷积来增强图像的局部信息。总之，膨胀卷积是一种非常有用的操作，能够有效改善网络的感受野，提升网络性能。

2、知识点

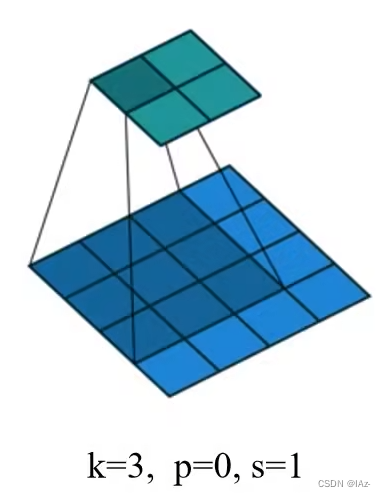
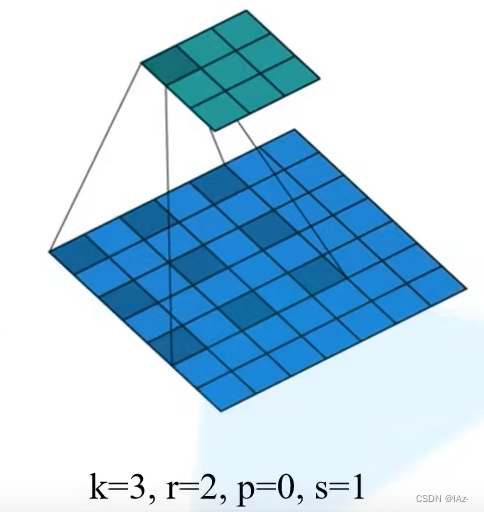
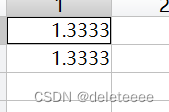
膨胀卷积与普通卷积同样使用[3x3]的卷积核，但是在膨胀卷积的卷积核中存在一定间隙，这个间隙在膨胀卷积中通常被称为膨胀因子 r。当r=1时，卷积核中元素处于相邻状态，即等同于普通卷积核。

膨胀卷积的优点：

增大感受野
通过增加padding来保持原输入特征图的高和宽

二、详细介绍

1、引入

使用膨胀卷积，在语义分割任务中，通常会使用分类网络作为语义分割网络的backbone，通过backbone之后会将原输入图片进行下采样，再通过一系列的上采样操作还原回原来大小。在分类网络中，通常会将原图像高宽下采样32倍，由于后期需要上采样还原到图像原尺寸，如果将特征图大小下采样倍率过大，对后期还原回原图大小很有影响。如VGG网络通过MaxPool层进行池化操作，通过MaxPool操作会降低特征图的高宽，其次会丢失细节信息以及小目标且无法通过上采样进行还原，会导致语义分割效果不理想。

若直接将MaxPool层舍去，会引入新问题，会导致得到特征图所对应原图的感受野变小。对应MaxPool层之后的卷积层原本是在之前对应的感受野之上做进一步操作，舍去MaxPool层会对之后的卷积层感受野造成影响。

使用膨胀卷积模块，既能增大感受野，并且可以保证输入输出特征图的高和宽不发生变化。但是在语义分割任务中也不可简单堆叠膨胀卷积模块。

膨胀卷积使用中会带来一个gridding effect问题。

对于膨胀卷积的使用有两种：

1）使用相同膨胀系数的情况下

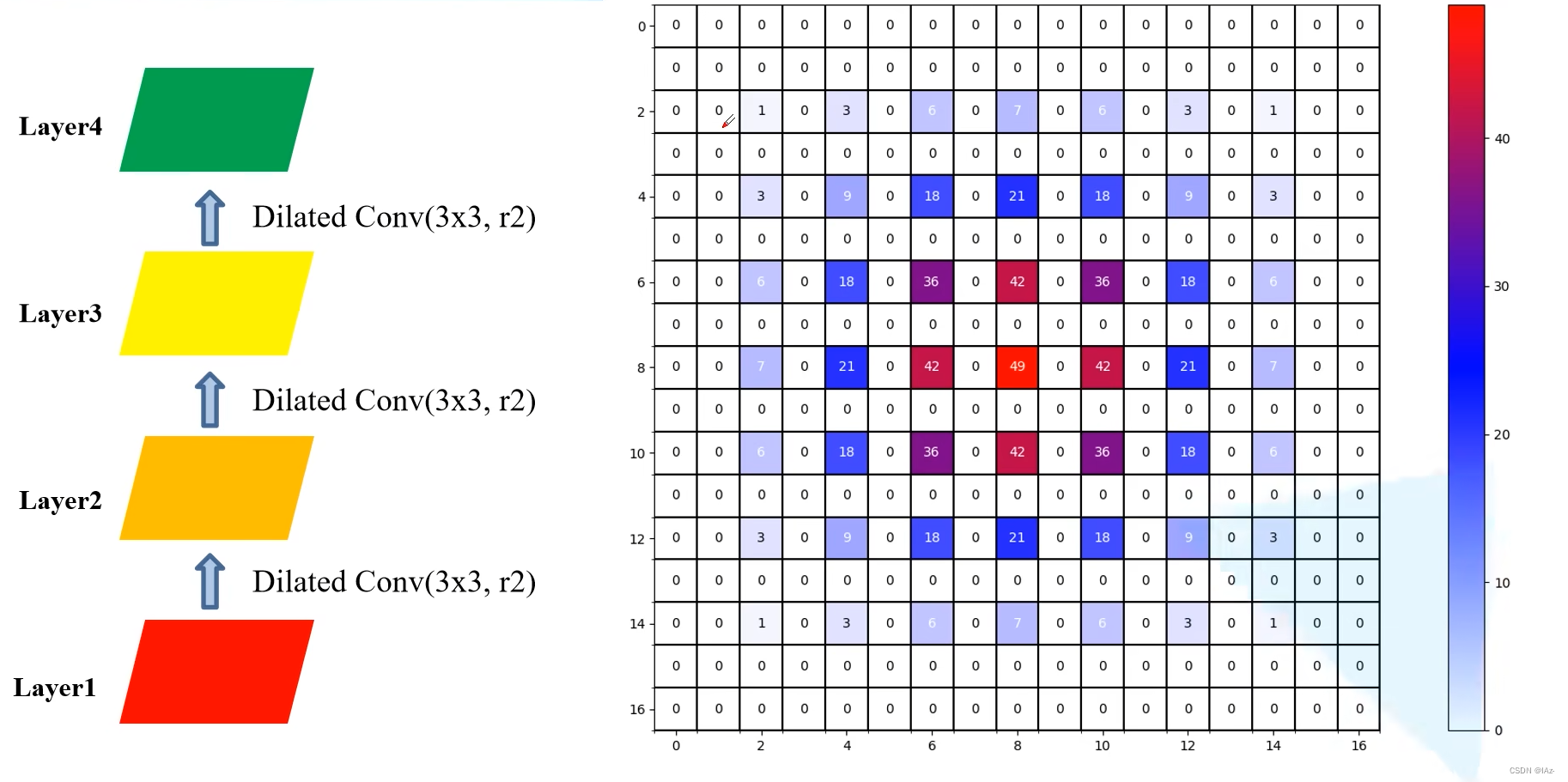
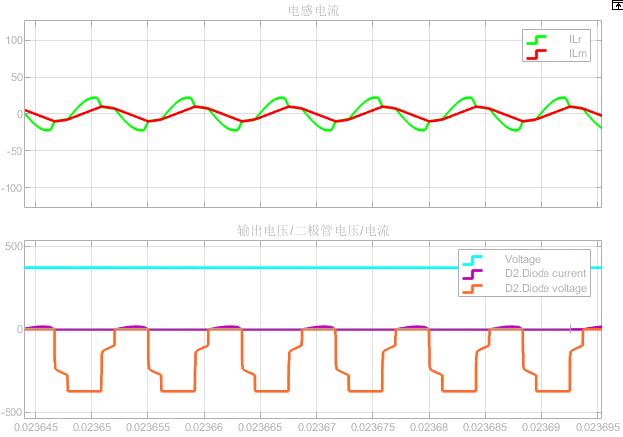
对于每层使用的膨胀卷积都使用相同膨胀系数r=2，右图是每一层的一个像素利用到Layer1上的对应像素。连续堆叠三个膨胀卷积层，可以发现Layer4上的一个像素利用到Layer1上的对应像素如右图的热图分布，并不是连续利用，每个非0元素之间都有一定间隔，并没有利用到范围内的所有像素值，造成细节信息丢失。即gridding effect现象。

2）使用不同膨胀系数的情况下

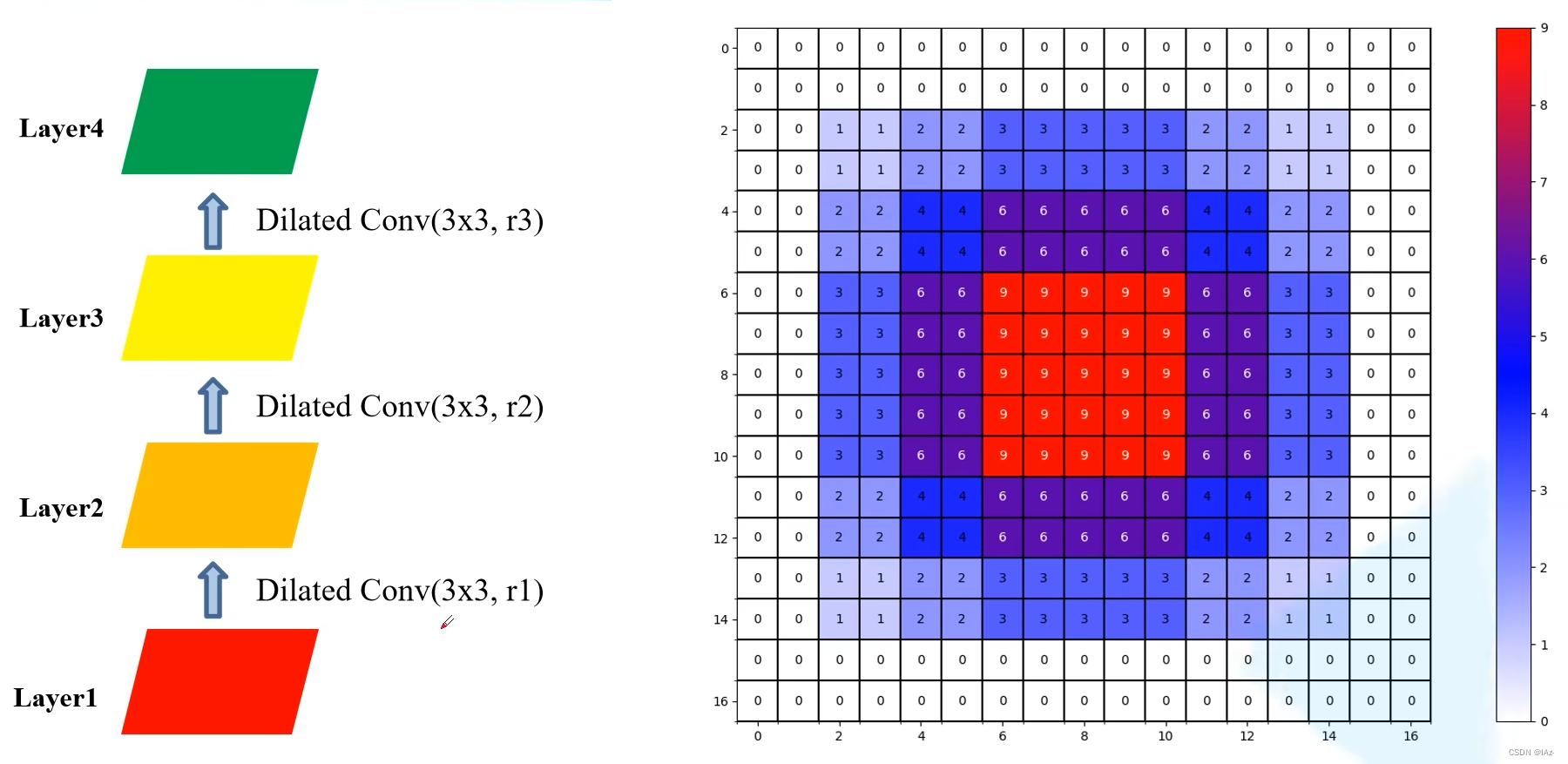
将膨胀系数分别设置成r=1，2，3。当r=1时膨胀卷积等同与普通卷积。则如图可以看出，Layer4上的一个像素利用到了Layer1上的13x13大小的像素，并且像素之间是相邻的，没有间隙和信息丢失。

3）使用膨胀系数r=1的情况

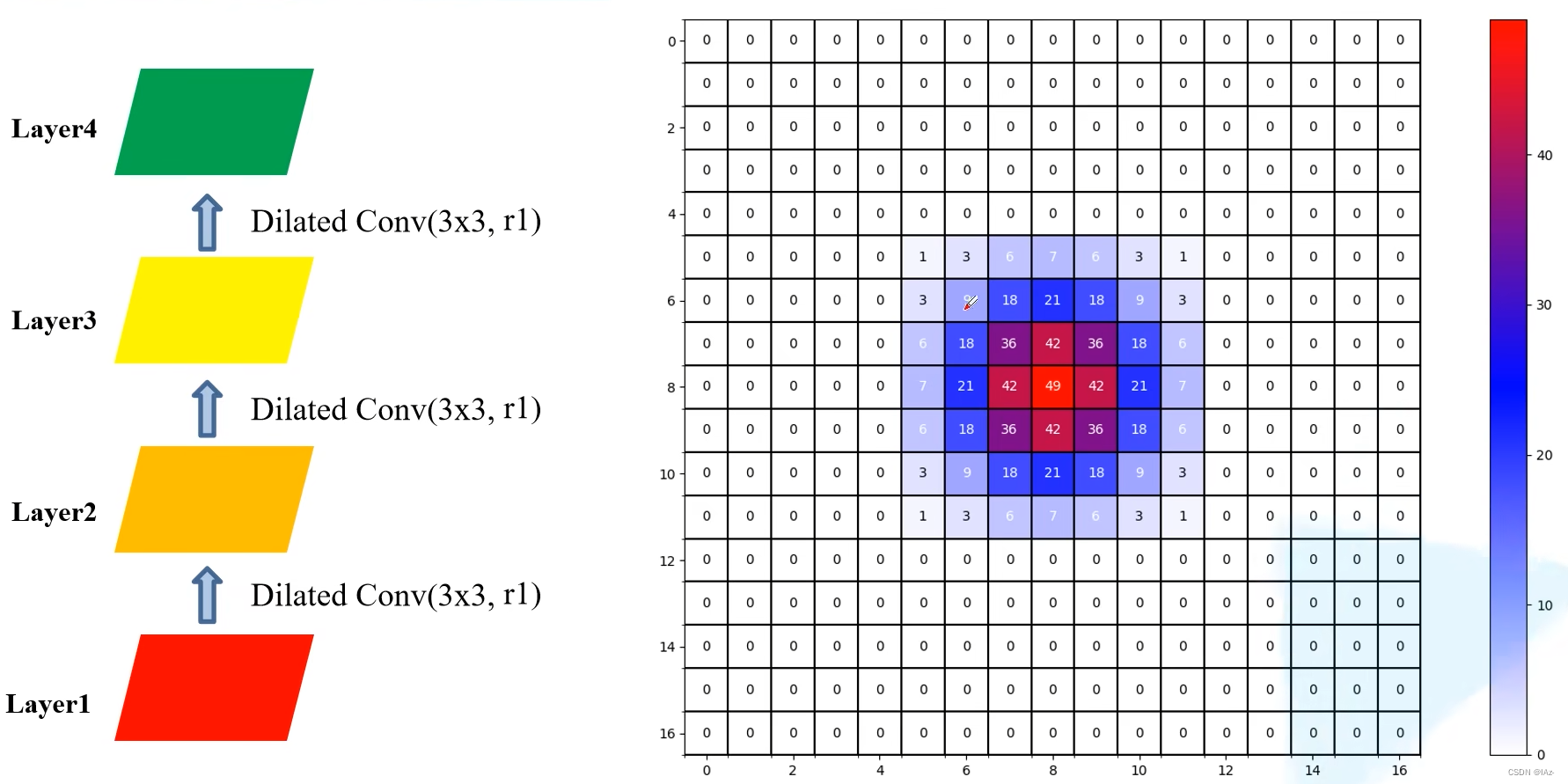
使用r=1膨胀卷积时即等同于使用普通卷积的情况，由图可以看出Layer4上的一个像素利用到了Layer1上像素仅占7x7大小的区域，感受野受限。

则在参数数量相同的情况下，在使用膨胀卷积之后感受野增大效果明显。

2、膨胀系数设定

当连续使用膨胀卷积时，膨胀系数的设定为r=1,2,3的情况下比设定为三个膨胀卷积的r=2的情况要好得多。

假设连续堆叠N个膨胀卷积，卷积核大小都为[K×K]，每一个膨胀卷积对应的膨胀系数为[ $r_{1},...,r_{i},...,r_{n}$ ]，则混合膨胀卷积HDC(Hybrid Dilated Convolution)的目标是通过一系列膨胀卷积之后，能够完全覆盖底层特征层上的一个方形区域，且之间无空隙。

1）Maximum Distance between two Nonzero Values最大非零元素之间距离

若在底层特征图上完全覆盖一个方形区域且无空隙，则此时非零元素之间的距离为1，当在底层特征图上覆盖区域有空隙时，则此时非零元素之间的距离为2，代表覆盖的方形区域之间是有空隙和间隔的。

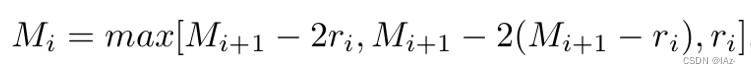
$M_{n}=r_{n}$ (n指代最后一个元素 $r_{n}$ ，n不代表一个顺序的泛指)

对于第i层所对应的非零元素之间最大距离。设计目标是让 $M_{2}\leq K$ 。比如说，当卷积核大小K=3时，r=[1,2,5]，则此时 $M_{2}=max[1,-1,2]=2$ ，则满足设计目标；又当r=[1,2,9]时，此时 $M_{2}=max[5,-5,2]=5$ ，不满足设计要求。且 $r_{1}=1$ .