目录
- 1.概述
- 2.代码实现
- 2.1.最基本的二分搜索
- 2.2.搜索最左侧边界
- 2.3.搜索最右侧边界
- 3.应用
本文参考:
LABULADONG 的算法网站
《大话数据结构》
1.概述
(1)二分搜索 (Binary Search),又称为折半搜索 (Half-interval Search)。它的前提是线性表中的记录必须是关键码有序(通常从小到大有序),线性表必须采用顺序存储。
(2)二分搜索的基本思想是:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功;若给定值小于中间记录的关键字,则在中间记录的左半区继续查找;若给定值大于中间记录的关键字,则在中间记录的右半区继续查找。不断重复上述过程,直到查找成功,或所有查找区域无记录,查找失败为止。
(3)二分搜索的时间复杂度为 O(log2n)。
2.代码实现
2.1.最基本的二分搜索
(1)最基本的二分搜索:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target,搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。实现代码如下:
class Solution {
public int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
//防止整数溢出
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
}
}
return -1;
}
}
该代码可以解决 LeetCode 中的704. 二分查找这题。
(2)大家肯定对上面的代码非常熟悉,不过这里需要其中的一些细节进行讨论:
① 在计算 mid 时,有以下两种方式:
int mid = (left + right) / 2;
int mid = left + (right - left) / 2;
这两种方法的计算结果相同,但需要注意的是:如果 left 和 right 的值非常大,那么 left + right 可能会出现整数溢出的情况,虽然该情况出现的概率比较低,但是从代码健壮性的角度来考虑,本文还是推荐使用第二种方式;
② while 循环条件写成 left <= right 和 left < right 的区别如下:
- 上述代码中的搜索区间为 [left, right],注意区间的两边均为闭区间,而 while (left <= right) 的终止条件是 left == right + 1,此时的区间表示为 [right + 1, right],这样的区间不存在,即此时的区间为空。所以此时 while 循环终止是正确的,直接返回 -1 即可。
- while (left < right) 的终止条件是 left == right,此时的区间表示为 [right, right](例如 right = 2,那么区间为 [2, 2])此时区间非空,还有一个数 2,但此时 while 循环终止了,
也就是说区间 [2, 2] 被漏掉了,索引为 2 的元素没有被搜索到,如果这时候直接返回 -1 就是错误的。 - 如果非要写成 while (left < right),那么直接在返回语句处稍作修改即可:
//...
while(left < right) {
// ...
}
return nums[left] == target ? left : -1;
③ 上述二分搜索代码的存在一定的局限性。例如,当 nums = {1, 4, 4, 4, 7},target = 4 时,此时返回的索引为 2,这没有问题。但是如果想得到 target 的最左/右侧边界的索引时(即分别对应索引 1 和索引 3),则该算法无法直接满足该要求,只能继续向左/右进行线性搜索,但是这样就无法保证二分搜索的对数级的时间复杂度。因此下面将讨论搜索 target 的最左/右侧边界的索引的情况。
2.2.搜索最左侧边界
(1)实现代码如下:
public int leftBoundSearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
//当 left > right 即 left = right + 1 时结束循环
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
right = mid - 1;
}
}
/*
检查 left 越界的情况:
当 target 比所有元素都大时,循环结束后 left = nums.length
*/
if (left >= nums.length || nums[left] != target) {
return -1;
}
return left;
}
(2)下面对该代码中的一些细节进行讨论:
① 在 while 循环中,当 nums[mid] == target 时:
- mid 未必就是 target 的最左侧边界索引(参考上面提到的例子),故不能直接返回 mid;
- 而由于我们想得到 target 的最左侧边界索引,且此时 nums[left…mid…right] 中的 nums[mid] 已经等于 target,那么接下来应该在 nums[left…mid - 1] 区间内进行搜索,所以要锁定左侧边界,并令 right = mid - 1;
- 如果此时的 mid 恰巧就是最左侧边界索引(记为 leftBound ),那么此时 nums[left…mid - 1] 区间内的元素均小于 target,所以在后面的搜索中只有 left 会通过 left = mid + 1 被不断更新,而 right = leftBound - 1保持不变。又由于当 left > right,即 left = right + 1 时结束循环,所以最终 left = leftBound - 1 + 1 = leftBound ;
② 当数组 nums 中不存在 target:
- target 比所有元素都大时,循环结束后 left = nums.length;
- 其它情况下,直接判断 nums[left] 是否等于 target 即可;
③ 代码中的两个 else if 语句其实用一个 else 语句代替,这里写出来主要是为了方便理解,合并后的代码如下:
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
2.3.搜索最右侧边界
(1)实现代码如下:
public int rightBoundSearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
//当 left > right 时结束循环
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] == target) {
left = mid + 1;
}
}
/*
检查 right 越界的情况:
当 target 比所有元素都小时,循环结束后 right 会被减到 -1
*/
if (right < 0 || nums[right] != target) {
return -1;
}
return right;
}
(2)下面对该代码中的一些细节进行讨论:
① 在 while 循环中,当 nums[mid] == target 时:
- mid 未必就是 target 的最右侧边界索引(参考上面提到的例子),故不能直接返回 mid;
- 而由于我们想得到 target 的最右侧边界索引,且此时 nums[left…mid…right] 中的 nums[mid] 已经等于 target,那么接下来应该在 nums[mid + 1…right] 区间内进行搜索,所以要锁定右侧边界,并令 left = mid + 1;
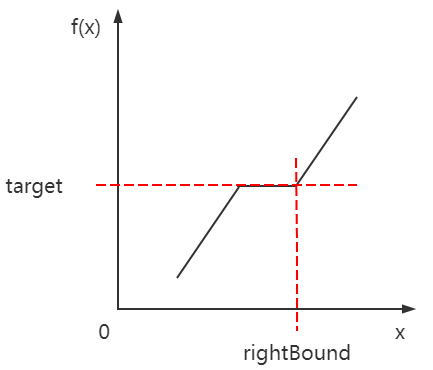
- 如果此时的 mid 恰巧就是最右侧边界索引(记为 rightBound),那么此时 nums[mid + 1…right] 区间内的元素均大于 target,所以在后面的搜索中只有 right 会通过 right = mid - 1 被不断更新,而 left = rightBound + 1保持不变。又由于当 left > right,即 right = left - 1 时结束循环,所以最终 right = rightBound+ 1 - 1 = rightBound;
② 当数组 nums 中不存在 target:
- target 比所有元素都小时,循环结束后 right = -1;
- 其它情况下,直接判断 nums[right] 是否等于 target 即可;
③ 代码中的两个 else if 语句其实用一个 else 语句代替,这里写出来主要是为了方便理解,合并后的代码如下:
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
注意:上面的最左/右侧边界讨论的均是数组 nums 中的元素为升序的情况,如果为降序,那么只需相应改变 if 条件中的比较符号即可。
3.应用
(1)可以使用二分搜索的关键在于:能够从问题中抽象出一个自变量 x,一个关于 x 的函数 f(x),以及一个目标值 target,并且 f(x) 必须是在 x 定义域上的单调函数(也可看做有序的),并且题目是要求出 f(x) == target 时的 x 的值(或者 x 的最左/右侧边界值)。
(2)这里以最基本的二分搜索(即 LeetCode 中的704. 二分查找这题)为例,分别找出对应的 x、f(x) 和 target:
| x | 数组 nums 的下标,其范围(定义域)为 [0, nums.length - 1] |
|---|---|
| f(x) | f(x) = nums[x],f(x) 是关于自变量 x 的函数,由于数组 nums 是有序的,所以 f(x) 在定义域上是单调的 |
| target | 题目中给的 target |
(3)从最基本的二分搜索中抽象出 x、f(x) 和 target 较为简单,下面再来看 LeetCode 中的875. 爱吃香蕉的珂珂这题:

分析如下:
| x | 吃香蕉的速度,即题中的 k |
|---|---|
| f(x) | 以速度 x 吃完香蕉所用的时间,并且它是单调递减的,即有序的(可以单独写一个函数来求解) |
| target | 警卫离开后回来的时间,即题中的 H |
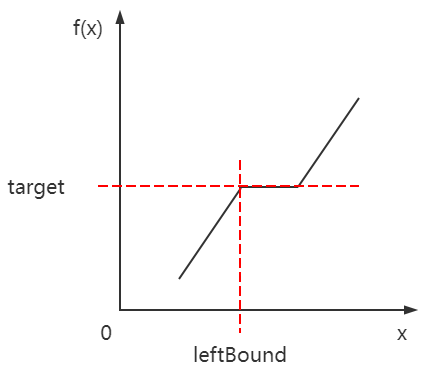
此外,需要注意的是,本题是要求 x/k 的最小值,那么即对应搜索 f(x) = target 时 x 的最左侧边界,对应的如下图所示:
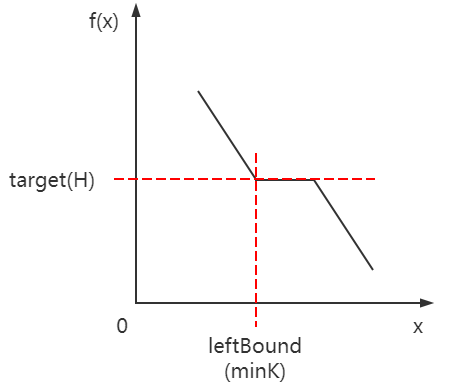
具体细节可以查看LeetCode_二分搜索_中等_875.爱吃香蕉的珂珂这篇文章,最终的实现代码如下:
//思路1————二分搜索
class Solution {
public int minEatingSpeed(int[] piles, int h) {
//maxK: 吃香蕉的最大速度
int maxK = piles[0];
for (int i = 1; i < piles.length; i++) {
if (piles[i] > maxK) {
maxK = piles[i];
}
}
//吃香蕉的最小速度为 1 根/小时,最大速度为 maxK 根/小时
int left = 1;
int right = maxK;
//查找左边界的二分搜索,计算吃完香蕉的最小速度
while (left <= right) {
int mid = left + (right - left) / 2;
if (getTime(piles, mid) > h) {
left = mid + 1;
} else {
right = mid - 1;
}
}
//由于本题一定有解,故不需要做边界判断
return left;
}
/*
实现 f(x)
k:吃香蕉的速度(单位:根/小时)
返回值:吃完所有香蕉所需的时间(单位:小时)
*/
public long getTime(int[] piles, int k) {
//防止整数溢出
long hour = 0;
for (int i = 0; i < piles.length; i++) {
hour += piles[i] / k;
if (piles[i] % k > 0) {
hour++;
}
}
return hour;
}
}
(4)读到这里,想必大家对二分搜索有了一定的了解,大家可以去 LeetCode 上找相关的二分搜索的题目来练习,或者也可以直接查看LeetCode算法刷题目录(Java)这篇文章中的二分搜索章节。如果大家发现文章中的错误之处,可在评论区中指出。