map、set如何用红黑树封装
- map、set应用:map是一个使用参数K、参数V的类模板,set是只使用参数K的类模板。因为map应用时,需要使用到KV,而set只是存单个值,K。
- 红黑树类的存储 :map和set类中使用红黑树数据成员:RBTree<> t;红黑树类型的数据成员,而红黑树类主要用两个模板参数K、V,(KeyOfT下面再讲)。此外红黑树类的内部有一个红黑树节点的数据成员,因为map存KV,set只需要存K的原因,红黑树类中的K、T在set内是:K、K,而map中是K、pair<K, V>。
- 红黑树节点的存储:红黑树的节点类只使用一个模板参数T。对于map,实例化时,节点的参数T只需要接收RBT传来的T值。因为它是pair键值对,map节点的KV都能得到。而set,实例化T为存的K。
关系图如下:
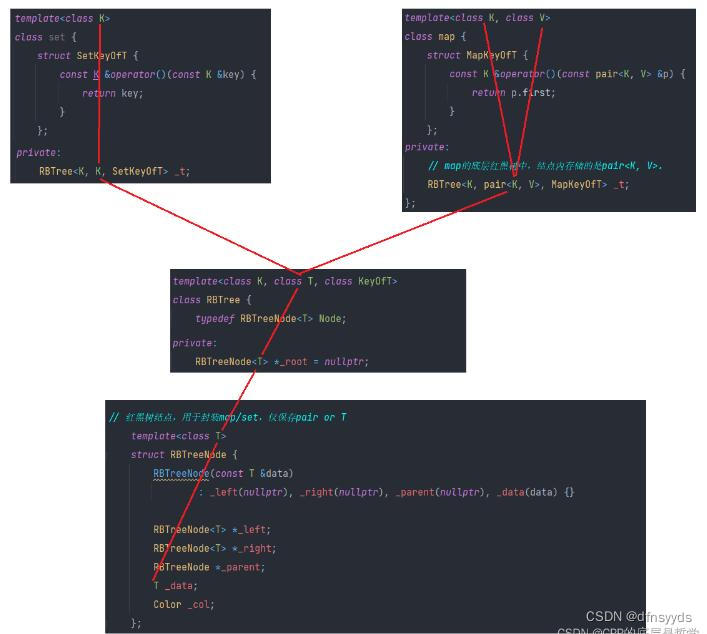
那么能不能不要RBTree中的第一个参数?反正map时,给RBTNode的参数T实例化为kv对能拿到两个,而set只有一个K,给RBTree的第二个参数和第一个参数的值都一样。
set可以满足,但是map容器的接口有些参数,只有Key值,不存在V,如find()、erase()
各类的定义:
为了与原来的红黑树模板参数区分,把RBTree的第二个参数换为V
enum Colour
{
RED,
BLACK
};
template<class K, class T>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
//构造函数
RBTree()
:_root(nullptr)
{}
private:
RBTreeNode<T>* _root = nullptr;
}
//红黑树结点的定义
template<class T>
struct RBTreeNode
{
//三叉链
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
//存储的数据
T _data;
//结点的颜色
int _col; //红/黑
//构造函数
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _col(RED)
{}
};
仿函数:RBT中使用
-
为什么要使用仿函数?
答:红黑树节点中存的是模板参数类型的 T _data,我们知道map实例RBTree传的<K, pair<K,V>,再给Node传:pair<K,V> ; 而set传给RBTree的是<K, K>,给Node传<K>。在调用RBT的find()时,传入的Key和每个节点的data做比较,如果是map类型,Node节点的data是个kv对,不能直接和find传的Key比较,map需要取出pair中的K,再比较。所以RBT需要仿函数去取节点的值,思路是:在map中的仿函数返回pair中的first,set中的仿函数返回第一个参数。 -
仿函数的写法:
仿函数需要重载operator(),map中重载()参数是KV对,返回引用类型的KV.first。如果在set()中,返回key。
如下,定义了两个不同名的仿函数类。
struct MapKeyOfT {
const K& operator()(const pair<K, V>& p) {
return p.first;
}
};
struct SetKeyOfT {
const K& operator()(const K& key) {
return key;
}
};
- 仿函数在哪使用?
- 定义:在map、set类中的RBTree类型成员变量和带着RBTree的重定义都要加入:
(map)RBTree<K, pair<K, V>, MapKeyOfT> _t;
(set)RBTree<K, K, SetKeyOfT> _t;
意思是:通过map、set实例化时,会传入不同的仿函数,所以在RBTree的各种函数中,可以通过仿函数拿到map、set值。
- RBTree的函数中,如find():使用仿函数类创建仿函数对象变量,直接传Node节点的data。
iterator find(const K& key) {
KeyOfT kot;
Node* root = _root;
while (root != nullptr) {
if (kot(root->_data) > key) {
root = root->_left;
}
else if (kot(root->_data) < key) {
root = root->_right;
}
else {
return iterator(root);
}
}
return iterator(nullptr);
}
- 图示:map、set分别传给RBTree不同的仿函数

迭代器类
迭代器类需要单独写出来。
正向迭代器定义:
template<class T, class Ref, class Ptr>
struct __RBTree_Iterator {
typedef RBTreeNode<T> Node;
Node* _node;
__RBTree_Iterator(Node* node)
: _node(node) {}
// 解引用迭代器,得到结点中的元素类型
Ref operator*() {
return _node->_data;
}
Ptr operator->() {
return &(_node->_data);
}
bool operator==(const __RBTree_Iterator<T, Ref, Ptr>& self) const {
return _node == self._node; // 比较迭代器里面结点指针的值,保存的是结点的地址。
}
bool operator!=(const __RBTree_Iterator& self) const {
return _node != self._node;
}
迭代器类分析
-
模板参数
因为需要区分普通类型迭代器和const类型迭代器,所以使用三个模板参数。 -
成员变量
迭代器的本质是节点类的地址,所以需要一个节点类型成员变量:Node* _node。此外,在内部typedef节点,为了方便调用。 -
重载解引用
返回引用类型的节点的data,因为当map时需要做修改value,所以这里把权限放出来。 -
重载->
返回指针类型的data值,返回节点存值的地址即可。 -
重载!=
比较的也是个迭代器类型的对象,当前对象有节点指针变量的成员,而参数也有节点指针变量成员,直接比较它们的node值相等否,相等则说明指向同一个节点地址。
迭代器的使用:RBTree
我们知道,map、set应该直接能调用迭代器类型的begin()、end(),而begin()、end()在RBTree中实现后,在map和set中直接调用即可。所以先在RBTree中实现迭代器方法,不然在map、set中会写两份冗余度极高的代码。
- RBTree中区分普通迭代器和const类型迭代器:
public:
typedef __RBTree_Iterator<T, T&, T*> iterator;
typedef __RBTree_Iterator<T, const T&, const T*> const_iterator;
RBTree中迭代器相关函数:
- begin():
红黑树是二叉搜索树,第一个节点,是最左孩子。返回迭代器类型的cur节点即可。
iterator begin()
{
//寻找最左结点
Node* left = _root;
while (left&&left->_left)
{
left = left->_left;
}
//返回最左结点的正向迭代器
return iterator(left);
}
- end():
end()应该返回空iterator(nullptr);
end()迭代器有点错误,它++或–,会有错误。STL中,有头结点。
iterator end()
{
//返回由nullptr构造得到的正向迭代器(不严谨)
return iterator(nullptr);
}
++:
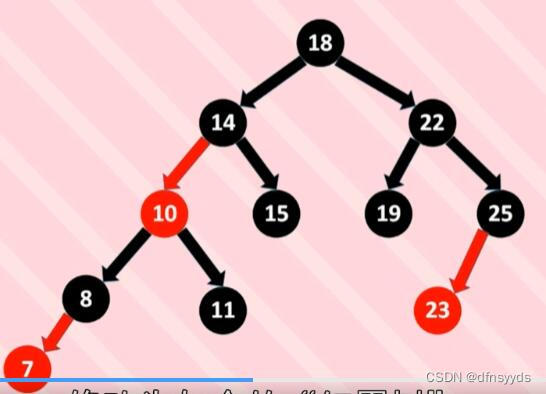
红黑树是搜索二叉树,中序满足升序,++应该向中序的后一位移动。
规则如下:以当前为标准,找大于当前的肯定是向右找。
- 右子树不为空,则访问最左孩子。
- 右子树为空,则访问符合条件的父节点,父亲节点满足:cur是父亲的非右孩子。
比如规则2,当前在7,左子树为空,那么++后应该找父节点的右孩子不是cur的父。而7是8的左孩子,那么8满足。
比如cur在11,11是10的右孩子,不行,cur变10,那么14是10的父亲且10不是右孩子,所以11的++是14。
- 代码写法:
- 右子树是否存在,存在则找最左。因为++是要向后走,找当前节点右孩子的最左。
- 右子树不存在,则循环更新直到走到规则2中的parent位置。
__RBTree_Iterator& operator++() // 迭代器前置++,使指针指向红黑树中序下一个值。
{
if (_node->_right) //结点的右子树不为空
{
//寻找该结点右子树当中的最左结点
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left; //++后变为该结点
}
else //结点的右子树为空
{
//寻找孩子不在父亲右的祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent&&cur == parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //++后变为该结点
}
return *this;
}
–:
–是要去前一个,往回倒,找小于它的,规则如下:
- 当前有左子树,则去最左子树的最右节点。
- 当前没有左子树,则去找特定的父亲。当前节点不能是父亲的左儿子即可。
如上,cur==8,有左孩子,则去7。
11没有左孩子,到10就可以了。而19是父亲的左孩子,则更新为父亲,父亲22不是18的左孩子,则18是符合条件的父亲。
- 代码步骤:
- 有左孩子,则找左孩子最右。
- 没有左孩子,找特定要求的父亲,更新cur不在父亲的左边时,更新cur为父亲。
- 代码
//前置--
Self operator--()
{
if (_node->_left) //结点的左子树不为空
{
//寻找该结点左子树当中的最右结点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = right; //--后变为该结点
}
else //结点的左子树为空
{
//寻找孩子不在父亲左的祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent&&cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //--后变为该结点
}
return *this;
}
在map中的使用正向迭代器
- begin()、end() 直接调用RBT的方法即可
public:
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator; //正向迭代器
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::reverse_iterator reverse_iterator; //反向迭代器
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
operator[]:参数:const K& key
map[]应该能对不存在的key做插入,或者直接修改已经存在的第二个值。
不论key存在否,insert()会返回迭代器、插入结果的pair。
first拿到迭代器,再通过迭代器的->拿到KV对,再利用KV->second拿到value,两个->可以缩成一个。
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
iterator it = ret.first;
return it->second;
}
在set中使用正向迭代器
set存储为单值,不需要提供什么【】。
public:
typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator; //正向迭代器
typedef typename RBTree<K, K, SetKeyOfT>::reverse_iterator reverse_iterator; //反向迭代器
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
反向迭代器
用正向迭代器封装。
insert():
红黑树中的inert()
- map和set底层是红黑树,利用红黑树的insert()即可。
- 这里红黑树节点中只有一个参数T,对于map时,需要取key做比较找合适位置,而set为了和map能通过仿函数做区分,所以map和set中找合适位置都需用仿函数去做比较。
仿函数使用是:把模板参数类型的T 变量和节点的data属性都传入仿函数做比较。
pair<Node*, bool> Insert(const T& kv)
{
if (_root == nullptr) //若红黑树为空树,则插入结点直接作为根结点
{
_root = new Node(kv);
_root->_col = BLACK; //根结点必须是黑色
return make_pair(_root, true); //插入成功
}
KeyOfT kot;
//1、按二叉搜索树的插入方法,找到待插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if(kot(kv) < kot(cur->_data)) //待插入结点的key值小于当前结点的key值
{
//往该结点的左子树走
parent = cur;
cur = cur->_left;
}
else if (kot(kv) > kot(cur->_data)) //待插入结点的key值大于当前结点的key值
{
//往该结点的右子树走
parent = cur;
cur = cur->_right;
}
else //已经存在
{
return make_pair(cur, false); //插入失败
}
}
//2、将待插入结点插入到树中
cur = new Node(kv); //根据所给值构造一个结点
Node* newnode = cur; //记录新插入的结点(便于后序返回)
if (kot(kv) < kot(parent->_data)) //新结点的key值小于parent的key值
{
//插入到parent的左边
parent->_left = cur;
cur->_parent = parent;
}
else //新结点的key值大于parent的key值
{
//插入到parent的右边
parent->_right = cur;
cur->_parent = parent;
}
//3、颜色调整:当新插节点默认是红,且父也红,连续红色则调整
while (parent && parent->_col == RED) { // 条件一定是父亲存在且父也红
Node* grandfather = parent->_parent;
Node* uncle = nullptr; // 定位uncle,根据父位判断叔
if (parent == grandfather->_left)
uncle = grandfather->_right;
else
uncle = grandfather->_left;
// 情况1:叔存在且红
if (uncle && uncle->_col == RED) {
// 叔叔存在且为红
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else {
// 情况2+3:叔叔不存在或者叔叔存在且为黑
if (parent == grandfather->_left && cur == parent->_left) // 左直线
{
// 此时,左左,右单旋+变色
// 先变色也可以
parent->_col = BLACK;
grandfather->_col = RED;
RotateR(grandfather);
}
else if (parent == grandfather->_right && cur == parent->_right) { // 右直线
// 右右,左单旋
parent->_col = BLACK;
grandfather->_col = RED;
RotateL(grandfather);
}
// 折线情况下,因为情况3的uncle不存在,且情况2uncle颜色不变
// 此外,情况2、3的折线翻转再变色后相同逻辑位置的cur、p、g最终颜色也一样
else if (parent == grandfather->_right && cur == parent->_left) {
// cur为红,parent为红,grandfather为黑。
// 右左双旋。
RotateR(parent);
RotateL(grandfather);
// 记住这里是上黑,下面俩红即可。
cur->_col = BLACK;
grandfather->_col = RED;
}
else if (parent == grandfather->_left && cur == parent->_right) {
RotateL(parent);
RotateR(grandfather);
// 记住这里是上黑,下面俩红即可。
cur->_col = BLACK;
grandfather->_col = RED;
/*RotateL(parent);
std::swap(cur, parent);
parent->_col = BLACK;
grandfather->_col = RED;
RotateR(grandfather);*/
}
break;
}
// 当前是根才做 直接做也行
if (cur == _root) {
cur->_col = BLACK;
}
}
return make_pair(newnode, true);
}
map中的insert
直接调用树的insert()。
pair<iterator, bool> insert(const pair<K, V>& kv) {
return _t.insert(kv);
}
set中的insert
直接调用树的insert()即可。
pair<iterator, bool> insert(const K& key) {
return _t.insert(key);
}
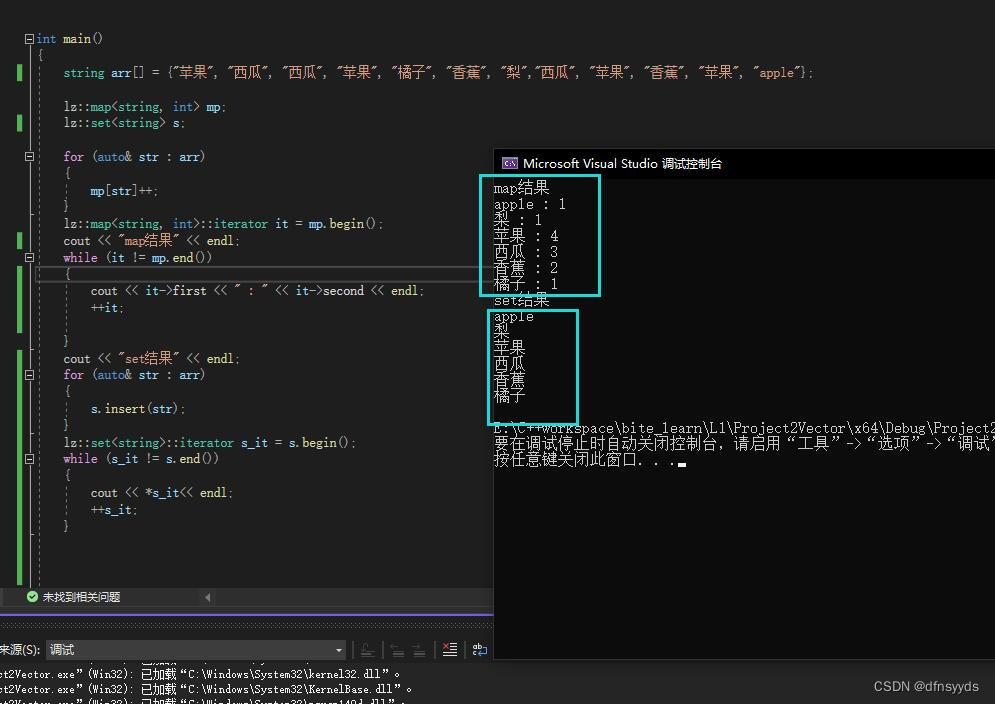
测试
#include "l8map.h"
#include "l8set.h"
int main()
{
string arr[] = {"苹果", "西瓜", "西瓜", "苹果", "橘子", "香蕉", "梨","西瓜", "苹果", "香蕉", "苹果", "apple"};
lz::map<string, int> mp;
lz::set<string> s;
for (auto& str : arr)
{
mp[str]++;
}
lz::map<string, int>::iterator it = mp.begin();
cout << "map结果" << endl;
while (it != mp.end())
{
cout << it->first << " : " << it->second << endl;
++it;
}
cout << "set结果" << endl;
for (auto& str : arr)
{
s.insert(str);
}
lz::set<string>::iterator s_it = s.begin();
while (s_it != s.end())
{
cout << *s_it<< endl;
++s_it;
}
return 0;
}
-
问题1:
枚举类型重定义、某个类重定义
解决办法:给每个.h文件中加#pragma once -
问题2:
我测试的时候,set方法没进去,仔细看,我的迭代器类型和set类型不一致。此外,我该给s用arr做insert()。还有就是set利用迭代器输出,解引用啊!!!
完整代码:
l8map.h
#pragma once
#include "l8RBTree.h"
namespace lz //防止命名冲突
{
template<class K, class V>
class map
{
//仿函数
struct MapKeyOfT
{
const K& operator()(const pair<K, V>& kv) //返回键值对当中的键值Key
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator; //正向迭代器
//typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::reverse_iterator reverse_iterator; //反向迭代器
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
//reverse_iterator rbegin()
//{
// return _t.rbegin();
//}
//reverse_iterator rend()
//{
// return _t.rend();
//}
//插入函数
pair<iterator, bool> insert(const pair<const K, V>& kv)
{
return _t.Insert(kv);
}
//[]运算符重载函数
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
iterator it = ret.first;
return it->second;
}
//删除函数
void erase(const K& key)
{
_t.Erase(key);
}
//查找函数
iterator find(const K& key)
{
return _t.Find(key);
}
private:
RBTree<K, pair<K, V>, MapKeyOfT> _t;
};
}
l8set.h
#pragma once
#include "l8RBTree.h"
namespace lz //防止命名冲突
{
template<class K>
class set
{
//仿函数
struct SetKeyOfT
{
const K& operator()(const K& key) //返回键值Key
{
return key;
}
};
public:
typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator; //正向迭代器
//typedef typename RBTree<K, K, SetKeyOfT>::reverse_iterator reverse_iterator; //反向迭代器
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
/*reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}*/
//插入函数
pair<iterator, bool> insert(const K& key)
{
return _t.Insert(key);
}
//删除函数
void erase(const K& key)
{
_t.Erase(key);
}
//查找函数
iterator find(const K& key)
{
return _t.Find(key);
}
private:
RBTree<K, K, SetKeyOfT> _t;
};
}
l8RBTree.h
#pragma once
#include<iostream>
#include<string>
using namespace std;
// 把这些都放进命名空间中
//枚举定义结点的颜色
namespace lz
{
enum Color
{
RED,
BLACK
};
//红黑树结点的定义
template<class T>
struct RBTreeNode
{
//三叉链
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
//存储的数据
T _data;
//结点的颜色
Color _col; //红/黑
//构造函数
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _col(RED)
{}
};
//正向迭代器
template<class T, class Ref, class Ptr>
struct __TreeIterator
{
typedef Ref reference; //结点指针的引用
typedef Ptr pointer; //结点指针
typedef RBTreeNode<T> Node; //结点的类型
typedef __TreeIterator<T, Ref, Ptr> Self; //正向迭代器的类型
Node* _node; //正向迭代器所封装结点的指针
//构造函数
__TreeIterator(Node* node)
:_node(node) //根据所给结点指针构造一个正向迭代器
{}
Ref operator*()
{
return _node->_data; //返回结点数据的引用
}
Ptr operator->()
{
return &_node->_data; //返回结点数据的指针
}
//判断两个正向迭代器是否不同
bool operator!=(const Self& s) const
{
return _node != s._node; //判断两个正向迭代器所封装的结点是否是同一个
}
//判断两个正向迭代器是否相同
bool operator==(const Self& s) const
{
return _node == s._node; //判断两个正向迭代器所封装的结点是否是同一个
}
//前置++
Self operator++()
{
if (_node->_right) //结点的右子树不为空
{
//寻找该结点右子树当中的最左结点
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left; //++后变为该结点
}
else //结点的右子树为空
{
//寻找孩子不在父亲右的祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //++后变为该结点
}
return *this;
}
//前置--
Self operator--()
{
if (_node->_left) //结点的左子树不为空
{
//寻找该结点左子树当中的最右结点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = right; //--后变为该结点
}
else //结点的左子树为空
{
//寻找孩子不在父亲左的祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //--后变为该结点
}
return *this;
}
};
//红黑树的实现
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node; //结点的类型
public:
typedef __TreeIterator<T, T&, T*> iterator; //正向迭代器
//typedef ReverseIterator<iterator> reverse_iterator; //反向迭代器
//reverse_iterator rbegin()
//{
// //寻找最右结点
// Node* right = _root;
// while (right && right->_right)
// {
// right = right->_right;
// }
// //返回最右结点的反向迭代器
// return reverse_iterator(iterator(right));
//}
//reverse_iterator rend()
//{
// //返回由nullptr构造得到的反向迭代器(不严谨)
// return reverse_iterator(iterator(nullptr));
//}
iterator begin()
{
//寻找最左结点
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
//返回最左结点的正向迭代器
return iterator(left);
}
iterator end()
{
//返回由nullptr构造得到的正向迭代器(不严谨)
return iterator(nullptr);
}
//构造函数
RBTree()
:_root(nullptr)
{}
//拷贝构造
RBTree(const RBTree<K, T, KeyOfT>& t)
{
_root = _Copy(t._root, nullptr);
}
//赋值运算符重载(现代写法)
RBTree<K, T, KeyOfT>& operator=(RBTree<K, T, KeyOfT> t)
{
swap(_root, t._root);
return *this; //支持连续赋值
}
//析构函数
~RBTree()
{
_Destroy(_root);
_root = nullptr;
}
//查找函数
iterator Find(const K& key)
{
KeyOfT kot;
Node* cur = _root;
while (cur)
{
if (key < kot(cur->_data)) //key值小于该结点的值
{
cur = cur->_left; //在该结点的左子树当中查找
}
else if (key > kot(cur->_data)) //key值大于该结点的值
{
cur = cur->_right; //在该结点的右子树当中查找
}
else //找到了目标结点
{
return iterator(cur); //返回该结点
}
}
return end(); //查找失败
}
//插入函数
pair<Node*, bool> Insert(const T& kv)
{
if (_root == nullptr) //若红黑树为空树,则插入结点直接作为根结点
{
_root = new Node(kv);
_root->_col = BLACK; //根结点必须是黑色
return make_pair(_root, true); //插入成功
}
KeyOfT kot;
//1、按二叉搜索树的插入方法,找到待插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kot(kv) < kot(cur->_data)) //待插入结点的key值小于当前结点的key值
{
//往该结点的左子树走
parent = cur;
cur = cur->_left;
}
else if (kot(kv) > kot(cur->_data)) //待插入结点的key值大于当前结点的key值
{
//往该结点的右子树走
parent = cur;
cur = cur->_right;
}
else //已经存在
{
return make_pair(cur, false); //插入失败
}
}
//2、将待插入结点插入到树中
cur = new Node(kv); //根据所给值构造一个结点
Node* newnode = cur; //记录新插入的结点(便于后序返回)
if (kot(kv) < kot(parent->_data)) //新结点的key值小于parent的key值
{
//插入到parent的左边
parent->_left = cur;
cur->_parent = parent;
}
else //新结点的key值大于parent的key值
{
//插入到parent的右边
parent->_right = cur;
cur->_parent = parent;
}
//3、颜色调整:当新插节点默认是红,且父也红,连续红色则调整
while (parent && parent->_col == RED) { // 条件一定是父亲存在且父也红
Node* grandfather = parent->_parent;
Node* uncle = nullptr; // 定位uncle,根据父位判断叔
if (parent == grandfather->_left)
uncle = grandfather->_right;
else
uncle = grandfather->_left;
// 情况1:叔存在且红
if (uncle && uncle->_col == RED) {
// 叔叔存在且为红
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else {
// 情况2+3:叔叔不存在或者叔叔存在且为黑
if (parent == grandfather->_left && cur == parent->_left) // 左直线
{
// 此时,左左,右单旋+变色
// 先变色也可以
parent->_col = BLACK;
grandfather->_col = RED;
RotateR(grandfather);
}
else if (parent == grandfather->_right && cur == parent->_right) { // 右直线
// 右右,左单旋
parent->_col = BLACK;
grandfather->_col = RED;
RotateL(grandfather);
}
// 折线情况下,因为情况3的uncle不存在,且情况2uncle颜色不变
// 此外,情况2、3的折线翻转再变色后相同逻辑位置的cur、p、g最终颜色也一样
else if (parent == grandfather->_right && cur == parent->_left) {
// cur为红,parent为红,grandfather为黑。
// 右左双旋。
RotateR(parent);
RotateL(grandfather);
// 记住这里是上黑,下面俩红即可。
cur->_col = BLACK;
grandfather->_col = RED;
}
else if (parent == grandfather->_left && cur == parent->_right) {
RotateL(parent);
RotateR(grandfather);
// 记住这里是上黑,下面俩红即可。
cur->_col = BLACK;
grandfather->_col = RED;
/*RotateL(parent);
std::swap(cur, parent);
parent->_col = BLACK;
grandfather->_col = RED;
RotateR(grandfather);*/
}
break;
}
// 当前是根才做 直接做也行
if (cur == _root) {
cur->_col = BLACK;
}
}
return make_pair(newnode, true);
}
//删除函数
bool Erase(const K& key)
{
KeyOfT kot;
//用于遍历二叉树
Node* parent = nullptr;
Node* cur = _root;
//用于标记实际的待删除结点及其父结点
Node* delParentPos = nullptr;
Node* delPos = nullptr;
while (cur)
{
if (key < kot(cur->_data)) //所给key值小于当前结点的key值
{
//往该结点的左子树走
parent = cur;
cur = cur->_left;
}
else if (key > kot(cur->_data)) //所给key值大于当前结点的key值
{
//往该结点的右子树走
parent = cur;
cur = cur->_right;
}
else //找到了待删除结点
{
if (cur->_left == nullptr) //待删除结点的左子树为空
{
if (cur == _root) //待删除结点是根结点
{
_root = _root->_right; //让根结点的右子树作为新的根结点
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //根结点为黑色
}
delete cur; //删除原根结点
return true;
}
else
{
delParentPos = parent; //标记实际删除结点的父结点
delPos = cur; //标记实际删除的结点
}
break; //进行红黑树的调整以及结点的实际删除
}
else if (cur->_right == nullptr) //待删除结点的右子树为空
{
if (cur == _root) //待删除结点是根结点
{
_root = _root->_left; //让根结点的左子树作为新的根结点
if (_root)
{
_root->_parent = nullptr;
_root->_col = BLACK; //根结点为黑色
}
delete cur; //删除原根结点
return true;
}
else
{
delParentPos = parent; //标记实际删除结点的父结点
delPos = cur; //标记实际删除的结点
}
break; //进行红黑树的调整以及结点的实际删除
}
else //待删除结点的左右子树均不为空
{
//替换法删除
//寻找待删除结点右子树当中key值最小的结点作为实际删除结点
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
cur->_data = minRight->_data; //将待删除结点的_data改为minRight的_data
delParentPos = minParent; //标记实际删除结点的父结点
delPos = minRight; //标记实际删除的结点
break; //进行红黑树的调整以及结点的实际删除
}
}
}
if (delPos == nullptr) //delPos没有被修改过,说明没有找到待删除结点
{
return false;
}
//记录待删除结点及其父结点(用于后续实际删除)
Node* del = delPos;
Node* delP = delParentPos;
//调整红黑树
if (delPos->_col == BLACK) //删除的是黑色结点
{
if (delPos->_left) //待删除结点有一个红色的左孩子(不可能是黑色)
{
delPos->_left->_col = BLACK; //将这个红色的左孩子变黑即可
}
else if (delPos->_right) //待删除结点有一个红色的右孩子(不可能是黑色)
{
delPos->_right->_col = BLACK; //将这个红色的右孩子变黑即可
}
else //待删除结点的左右均为空
{
while (delPos != _root) //可能一直调整到根结点
{
if (delPos == delParentPos->_left) //待删除结点是其父结点的左孩子
{
Node* brother = delParentPos->_right; //兄弟结点是其父结点的右孩子
//情况一:brother为红色
if (brother->_col == RED)
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateL(delParentPos);
//需要继续处理
brother = delParentPos->_right; //更新brother(否则在本循环中执行其他情况的代码会出错)
}
//情况二:brother为黑色,且其左右孩子都是黑色结点或为空
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//需要继续处理
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//情况三:brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空
if ((brother->_right == nullptr) || (brother->_right->_col == BLACK))
{
brother->_left->_col = BLACK;
brother->_col = RED;
RotateR(brother);
//需要继续处理
brother = delParentPos->_right; //更新brother(否则执行下面情况四的代码会出错)
}
//情况四:brother为黑色,且其右孩子是红色结点
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_right->_col = BLACK;
RotateL(delParentPos);
break; //情况四执行完毕后调整一定结束
}
}
else //delPos == delParentPos->_right //待删除结点是其父结点的左孩子
{
Node* brother = delParentPos->_left; //兄弟结点是其父结点的左孩子
//情况一:brother为红色
if (brother->_col == RED) //brother为红色
{
delParentPos->_col = RED;
brother->_col = BLACK;
RotateR(delParentPos);
//需要继续处理
brother = delParentPos->_left; //更新brother(否则在本循环中执行其他情况的代码会出错)
}
//情况二:brother为黑色,且其左右孩子都是黑色结点或为空
if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))
&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK)))
{
brother->_col = RED;
if (delParentPos->_col == RED)
{
delParentPos->_col = BLACK;
break;
}
//需要继续处理
delPos = delParentPos;
delParentPos = delPos->_parent;
}
else
{
//情况三:brother为黑色,且其右孩子是红色结点,左孩子是黑色结点或为空
if ((brother->_left == nullptr) || (brother->_left->_col == BLACK))
{
brother->_right->_col = BLACK;
brother->_col = RED;
RotateL(brother);
//需要继续处理
brother = delParentPos->_left; //更新brother(否则执行下面情况四的代码会出错)
}
//情况四:brother为黑色,且其左孩子是红色结点
brother->_col = delParentPos->_col;
delParentPos->_col = BLACK;
brother->_left->_col = BLACK;
RotateR(delParentPos);
break; //情况四执行完毕后调整一定结束
}
}
}
}
}
//进行实际删除
if (del->_left == nullptr) //实际删除结点的左子树为空
{
if (del == delP->_left) //实际删除结点是其父结点的左孩子
{
delP->_left = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
else //实际删除结点是其父结点的右孩子
{
delP->_right = del->_right;
if (del->_right)
del->_right->_parent = delP;
}
}
else //实际删除结点的右子树为空
{
if (del == delP->_left) //实际删除结点是其父结点的左孩子
{
delP->_left = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
else //实际删除结点是其父结点的右孩子
{
delP->_right = del->_left;
if (del->_left)
del->_left->_parent = delP;
}
}
delete del; //实际删除结点
return true;
}
private:
//拷贝树
Node* _Copy(Node* root, Node* parent)
{
if (root == nullptr)
{
return nullptr;
}
Node* copyNode = new Node(root->_data);
copyNode->_parent = parent;
copyNode->_left = _Copy(root->_left, copyNode);
copyNode->_right = _Copy(root->_right, copyNode);
return copyNode;
}
//析构函数子函数
void _Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}
//左单旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* parentParent = parent->_parent;
//建立subRL与parent之间的联系
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
//建立parent与subR之间的联系
subR->_left = parent;
parent->_parent = subR;
//建立subR与parentParent之间的联系
if (parentParent == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
//右单旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* parentParent = parent->_parent;
//建立subLR与parent之间的联系
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
//建立parent与subL之间的联系
subL->_right = parent;
parent->_parent = subL;
//建立subL与parentParent之间的联系
if (parentParent == nullptr)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
//左右双旋
void RotateLR(Node* parent)
{
RotateL(parent->_left);
RotateR(parent);
}
//右左双旋
void RotateRL(Node* parent)
{
RotateR(parent->_right);
RotateL(parent);
}
Node* _root; //红黑树的根结点
};
}
l8map_set.cpp
#include "l8map.h"
#include "l8set.h"
int main()
{
string arr[] = {"苹果", "西瓜", "西瓜", "苹果", "橘子", "香蕉", "梨","西瓜", "苹果", "香蕉", "苹果", "apple"};
lz::map<string, int> mp;
lz::set<string> s;
for (auto& str : arr)
{
mp[str]++;
}
lz::map<string, int>::iterator it = mp.begin();
cout << "map结果" << endl;
while (it != mp.end())
{
cout << it->first << " : " << it->second << endl;
++it;
}
cout << "set结果" << endl;
for (auto& str : arr)
{
s.insert(str);
}
lz::set<string>::iterator s_it = s.begin();
while (s_it != s.end())
{
cout << *s_it<< endl;
++s_it;
}
return 0;
}