文章目录
- [1.复原 IP 地址](https://leetcode.cn/problems/restore-ip-addresses/description/)
- 2.子集
- [3.子集 II](https://leetcode.cn/problems/subsets-ii/)
1.复原 IP 地址

切割问题可以使用回溯,本题分别两步,切割字符串和判断IP
切割逻辑如下:递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置
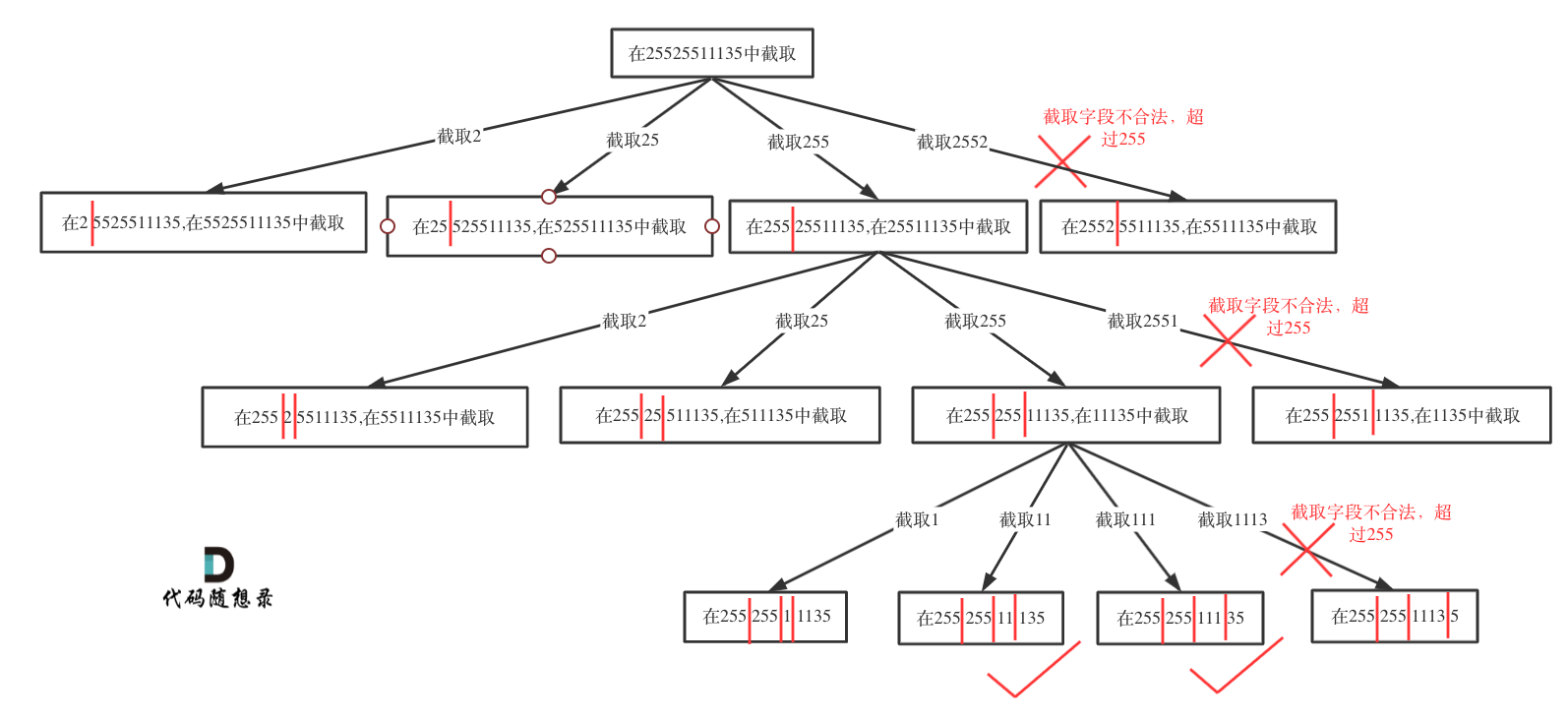
代码如下
class Solution {
private:
vector<string> result;
void backtracking(string&s, int startIndex, int pointNum) {
if (pointNum == 3) {
if (isValid(s, startIndex, s.size() - 1 )) {
result.push_back(s);
}
}
for (int i = startIndex; i < s.size(); i++) {
if(isValid(s, startIndex, i)) {
s.insert(s.begin() + i + 1 , '.');
pointNum++;
backtracking(s, i + 2, pointNum);
pointNum--;
s.erase(s.begin() +i + 1);
}
else break;
}
}
bool isValid (string& s, int start, int end) {//判断有效IP
if (start > end) return false;
if (s[start] == '0' && start != end) return false;
int num = 0;
for (int i = start; i <= end; i++) {
if (s[i] > '9' || s[i] < '0') return false;
num = num * 10 + s[i] - '0';
if (num > 255) return false;
}
return true;
}
public:
vector<string> restoreIpAddresses(string s) {
result.clear();
if (s.size() < 4 || s.size() > 12) return result; // 剪枝了
backtracking(s, 0, 0);
return result;
}
};
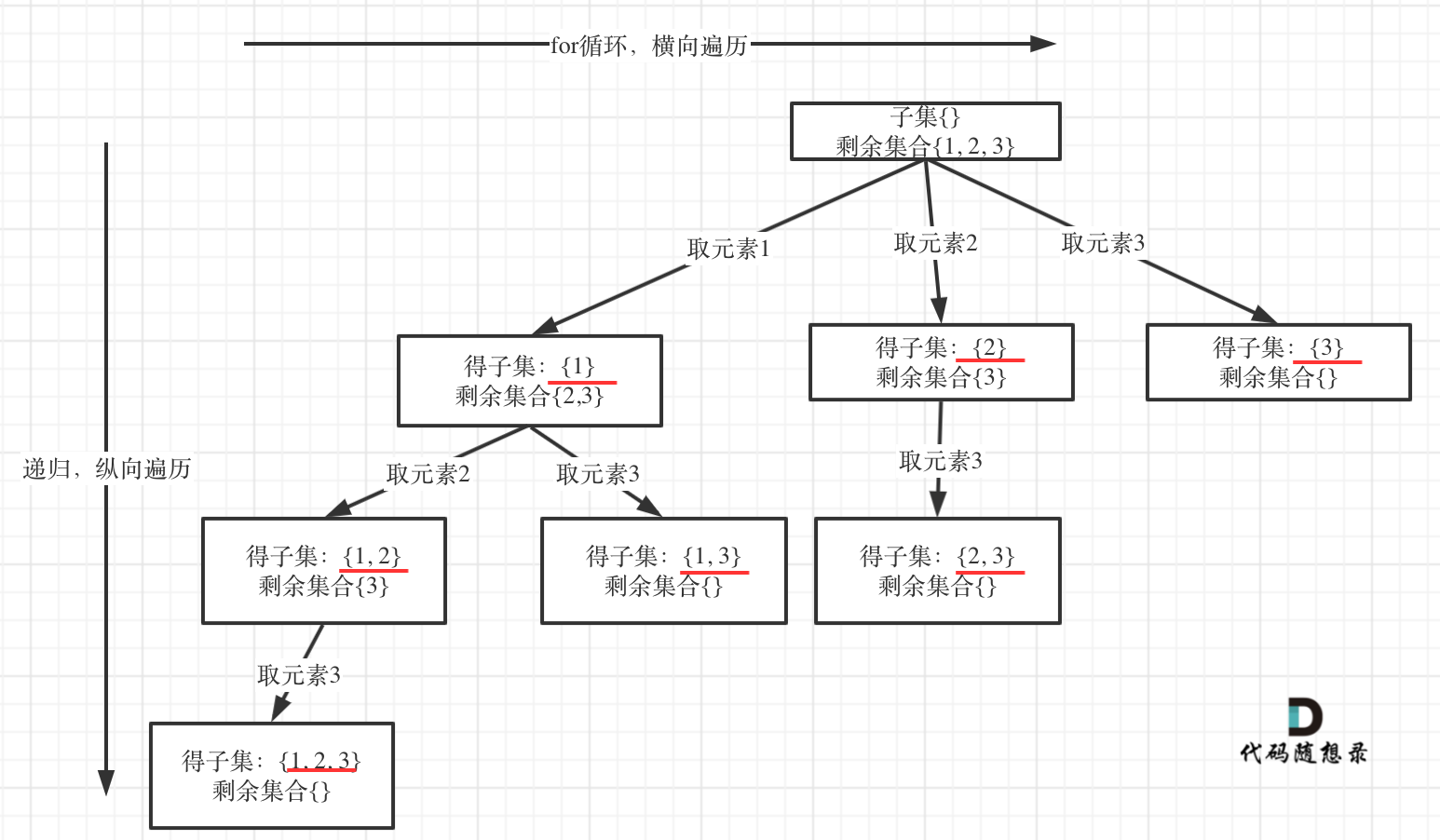
2.子集

分割问题找树的叶子节点
回溯法
代码如下
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
result.push_back(path);
if (startIndex > nums.size()) {//startIndex已经大于数组的长度为终止
return;
}
for (int i = startIndex; i < nums.size(); i++) {
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> subsets(vector<int>& nums) {
result.clear();
path.clear();
backtracking(nums, 0);
return result;
}
};
3.子集 II

只比
78.子集多了一个去重,我们要去掉同一树层的相同元素,保留同一树枝的。如下图
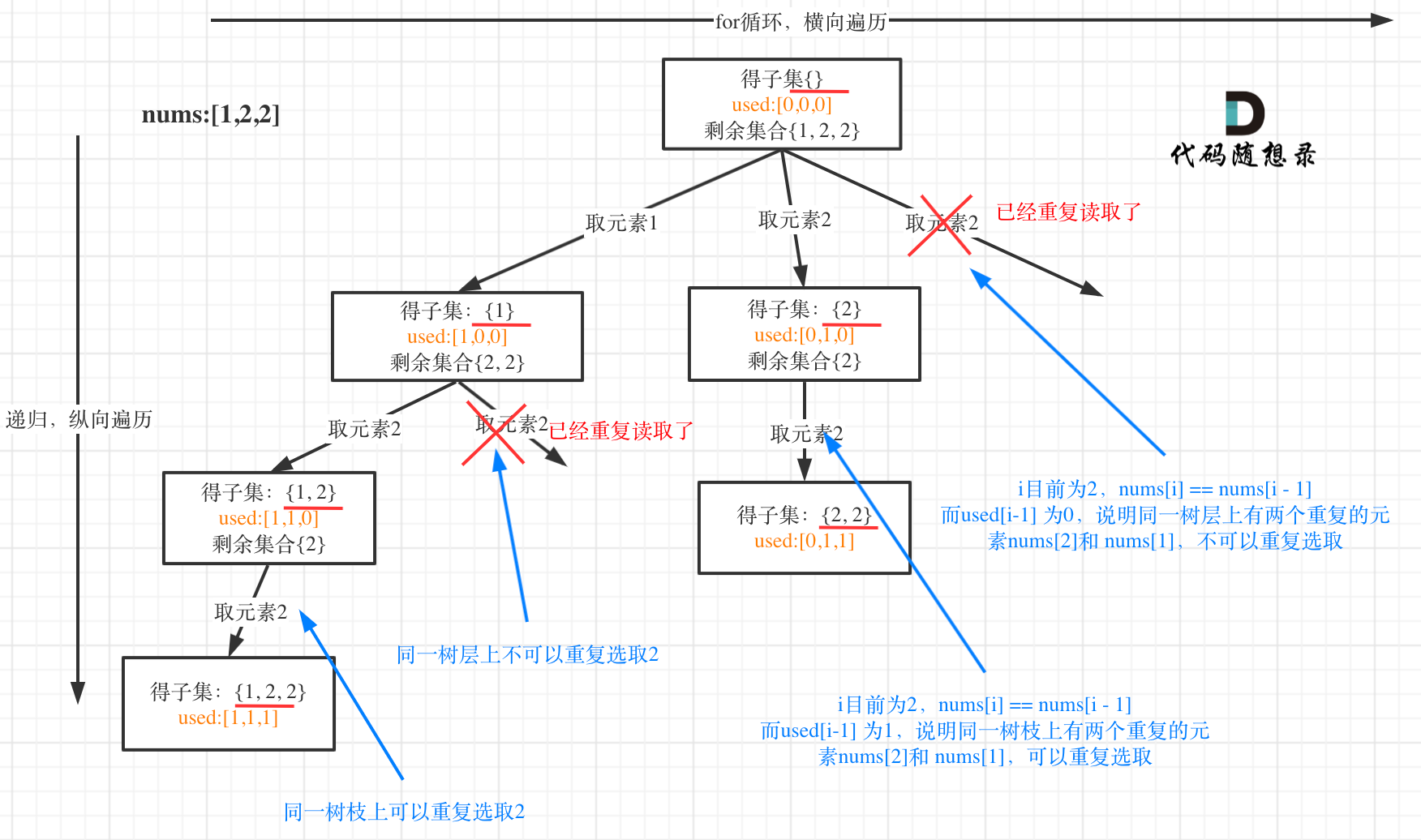
代码如下
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
if (startIndex > nums.size()) {
return;
}
for (int i = startIndex; i < nums.size(); i++) {
//同一树枝可重复取,但同一树层不可
if(i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
path.push_back(nums[i]);
used[i] = true;
backtracking(nums, i + 1, used);
used[i] = false;
path.pop_back();
}
}
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
backtracking(nums, 0, used);
return result;
}
};