第一范式
关系中的每一个分量必须是一个不可分的数据项。通俗地说,第一范式就是表中不允许有小表的存在。比如,对于如下的员工表,就不属于第一范式:
第二范式
实例
用一个单一的关系模式学生来描述学校的教务系统:学生(学号,学生姓名,系号,系主任姓名,课程号,成绩)
依赖关系(学号->学生姓名,学号->系号,系号->系主任姓名,(学生,课程号)>成绩)
 概念
概念
如果关系 R 属于1NF,且每一个非主属性完全函数依赖于任何一个候选码,则 R 属于2NF。
通俗地说,2NF 就是在 1NF 的基础上,表中的每一个非主属性不会依赖复合主键中的某一个列。(非主属性和主键之间不存在部分函数依赖)
按照定义,上面的学生表就不满足2NF,因为表的主键是复合主键(学号,课程号),但学号单独就能确定学生姓名,所在系等非主属性,所以非主属性和主键之间存在部分函数依赖。
第三范式
在满足 2NF 的基础上,表中不存在非主属性对主键的传递依赖。
继续上面的实例,学生关系模式就不属于3NF,因为学生无法直接决定系主任和系名,是由学号->系编号,再由系编号->系主任,系编号->系名,因此存在非主属性对主属性的传递依赖,
将学生表进一步分解为:
学生(学号,学生姓名,系编号) 系(系编号,系名,系主任)
选课(学号,课程号,成绩)每张表都属于3NF。
BC范式
BC范式 BCNF,是指在第三范式的基础上进一步消除主属性对于主键的部分函数依赖和传递依赖。
通俗的来说,就是在每一种情况下,每一个依赖的左边决定因素都必然包含候选键,如下:
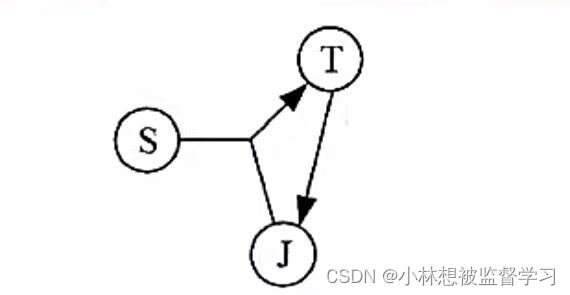
上图中,候选键有两种情况:组合键 (S,T) 或者 (S,J),依赖集为 {SJ—T,T—J },可知,STJ三个属性都是主属性,因此其达到了3NF(无非主属性),然而,第二种情况,即(S,J)为候选键的时候,对于依赖T->J,T在这种情况不是候选键,即 T-J 的决定因素不包含任意候选码,因此上图不是BCNF。
要使上图关系模式转换为 BCNF 也很简单,只需要将依赖 T->J 变为 TS->J 即可,这样其左边决定因素就包含了候选键之一 S 。