不知道你是否使用过IDA的条件断点呢?在IDA进阶使用中,它的很多功能都有大作用,比如:ida-trace来跟踪调用流程。同时IDA的断点功能也十分强大,配合IDA-python的输出语句能够大杀特杀!
那么本文就介绍一下这个功能点,使用z3来秒解题目。
条件断点
什么是条件断点呢?
条件断点(Conditional
Breakpoint)是一种在代码调试过程中设置的断点,它可以根据特定的条件暂停程序的执行。当程序执行到设置了条件断点的代码行时,如果该条件为真,则程序会暂停执行;如果该条件为假,则程序会继续执行。这种调试技术常用于复杂的程序调试,能够帮助程序员更快地发现程序中的错误,并提高调试的效率。条件断点可以应用于多种编程语言和开发环境中,如C++、Java、Python等。
与普通的断点大差不差,不同点在于,程序运行到条件断点处时,不会让程序暂停,而是继续执行,并执行我们设置好的脚本。
OK,接下来让我们分析这道题目
初次分析
main函数
flag的格式

打开main函数,发现使用了SIMD指令赋值了一些关键数据
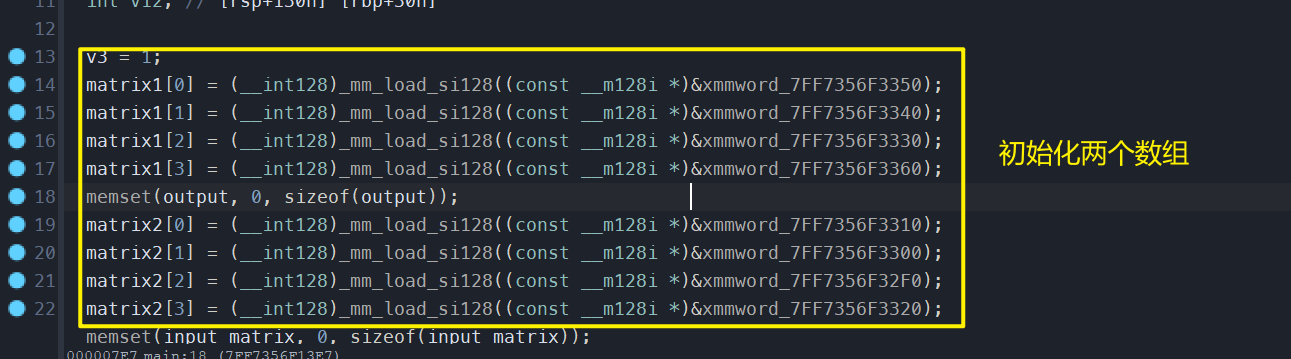
继续分析

看来cry1和cry2是很关键的函数
密文:

cry1
发现对我们的输入flag,进行一些转换:
比如:位置顺序和对我们的flag异或一个固定的值。
异或的值是由上下文决定的,但是总是单字节固定
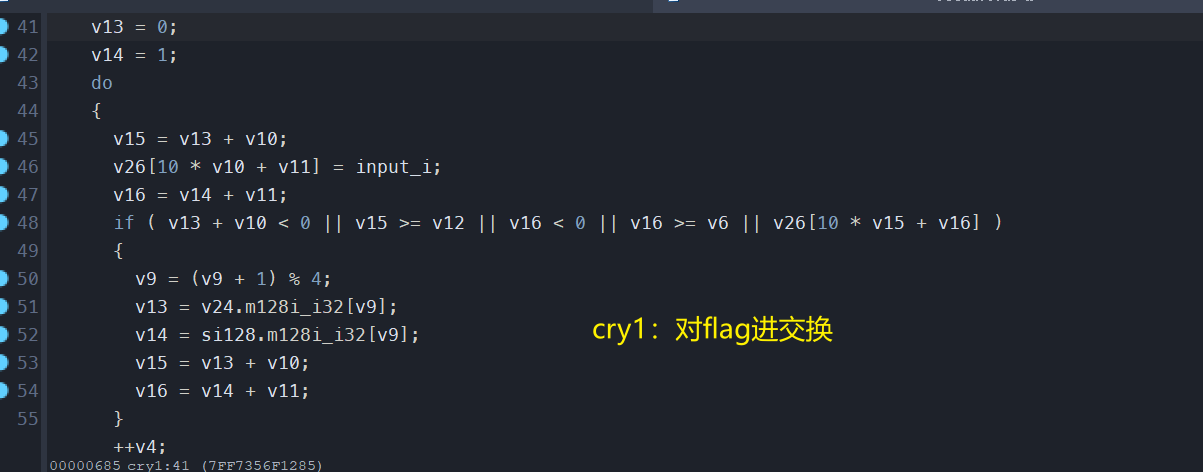
将输入的flag运算完后,转换为 一个int类型的矩阵
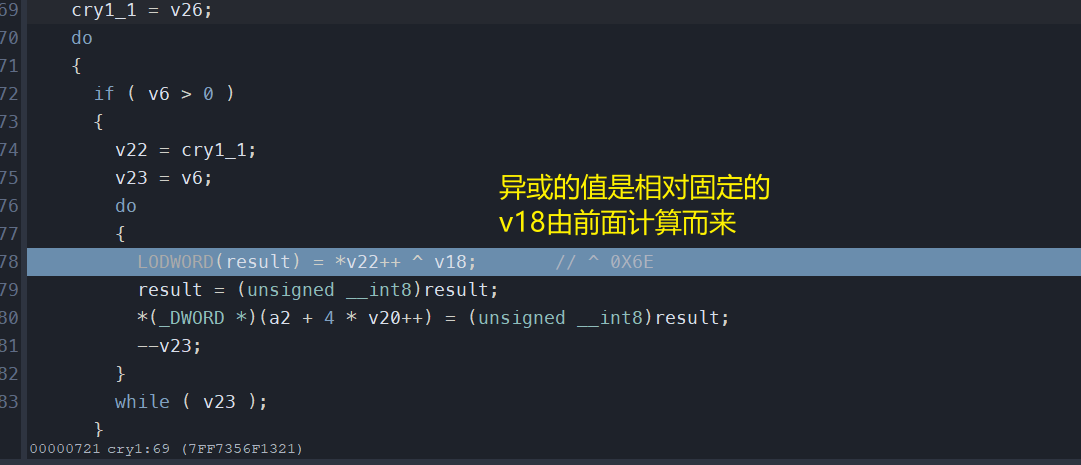
初次分析到此结束
帮助网安学习,全套资料S信免费领取:
① 网安学习成长路径思维导图
② 60+网安经典常用工具包
③ 100+SRC分析报告
④ 150+网安攻防实战技术电子书
⑤ 最权威CISSP 认证考试指南+题库
⑥ 超1800页CTF实战技巧手册
⑦ 最新网安大厂面试题合集(含答案)
⑧ APP客户端安全检测指南(安卓+IOS)
cry2
条件断点妙用
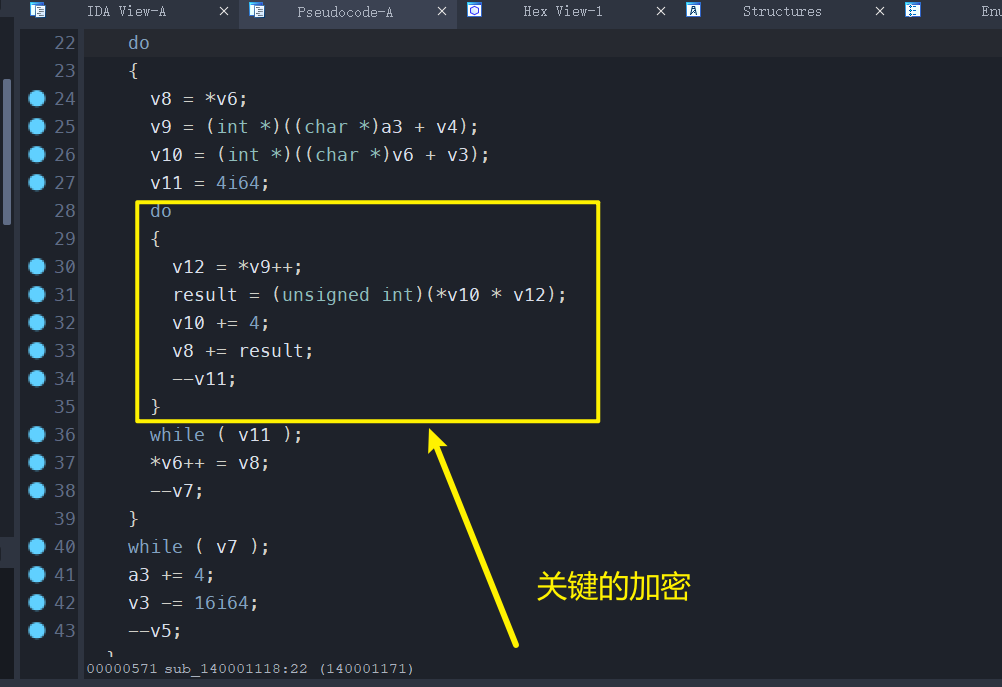
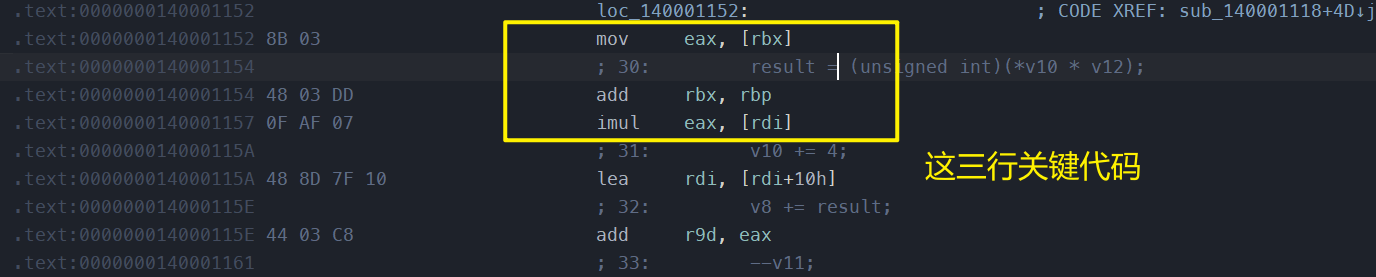
经过动调,我发现关键的加密就这三个汇编指令。
意思:取flag->与一个固定的矩阵相乘->输出加密之后的矩阵
如果我们能够打印,加密前的flag和相乘的矩阵元素,就可以逆推明文啦
主要是不清楚,矩阵相乘的顺序,可能是打乱的,那样只能这样来做。
使用了:条件断点
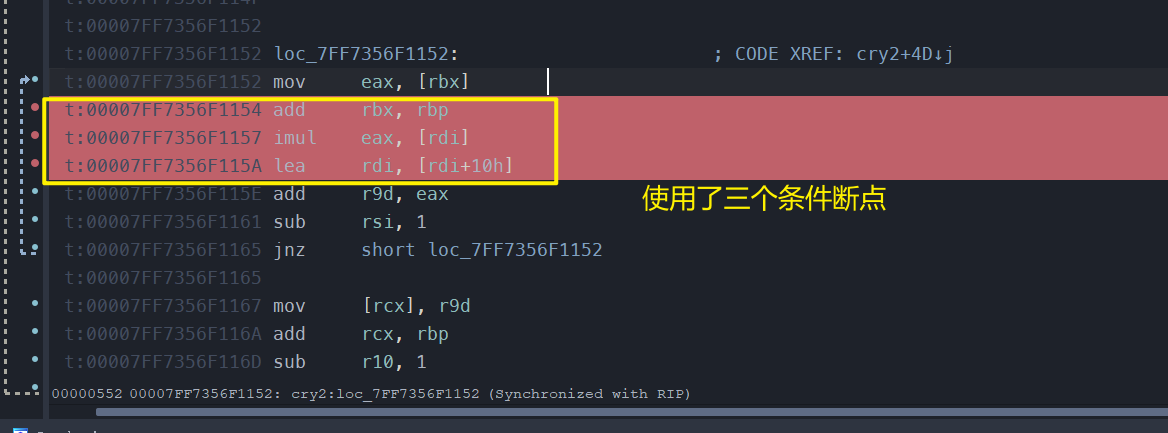
这三个断点依次使用下面3个条件输出
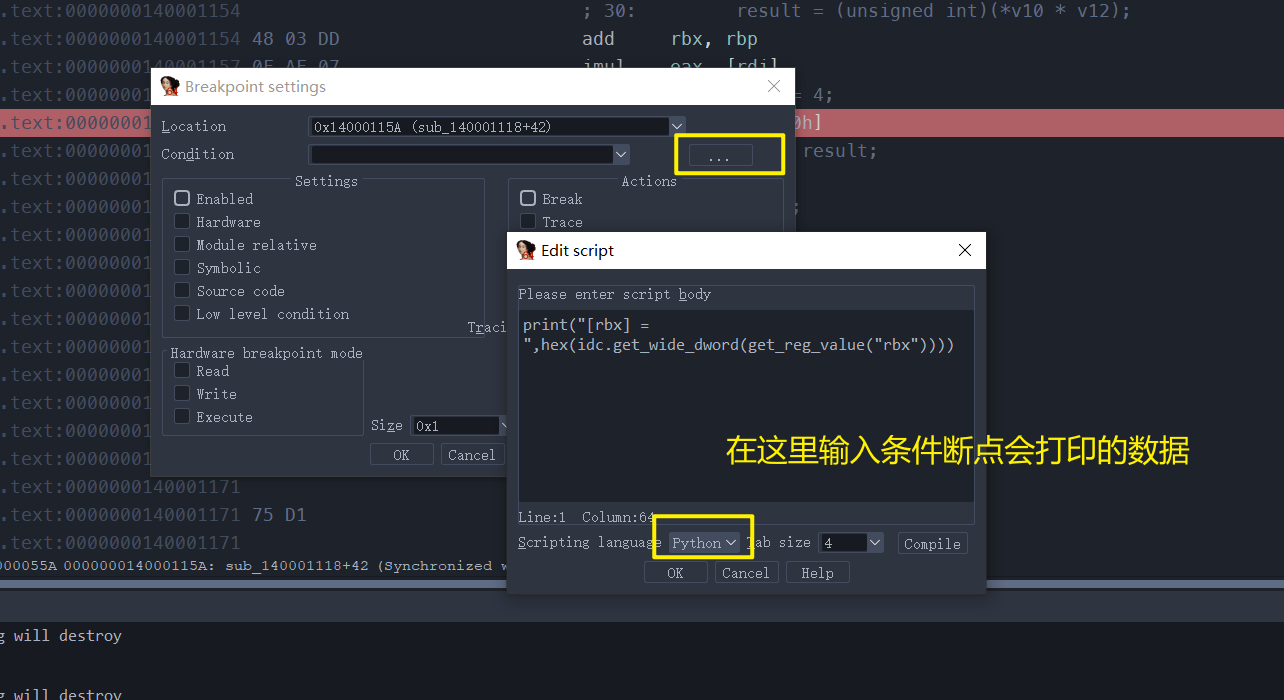
主要是这两个命令:
get_reg_value(“rbx”) 获取rbx寄存器的值
idc.get_wide_dword() 获取某地址的值(4字节读取)
print("[rbx] = ",hex(idc.get_wide_dword(get_reg_value("rbx"))))
print("rax = ",hex(get_reg_value("rax")),"[rdi]=
",hex(idc.get_wide_dword(get_reg_value("rdi"))))
print("output,rax = ",hex(get_reg_value("rax")),"n")
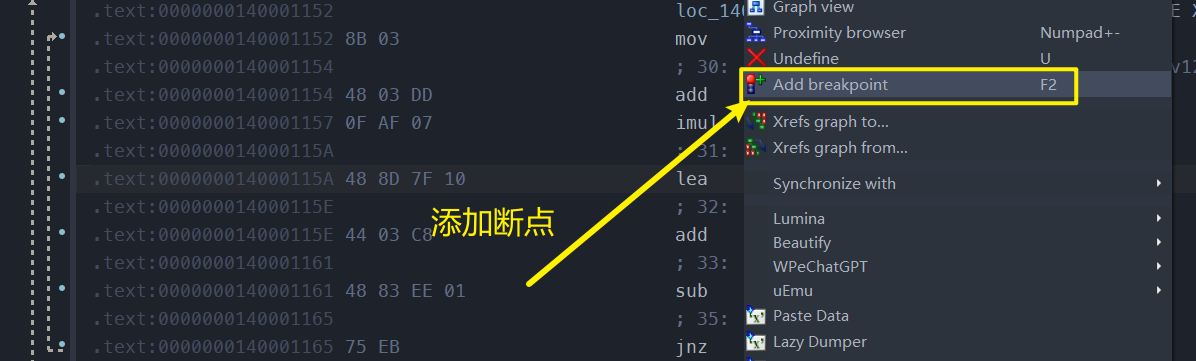
然后edit breakpoint
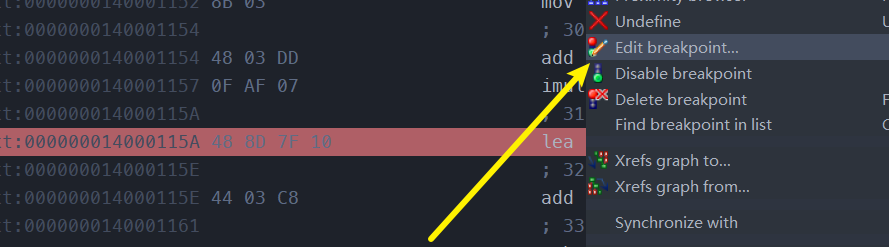
OK,见证奇迹的时刻到了,运行程序,成功输出:
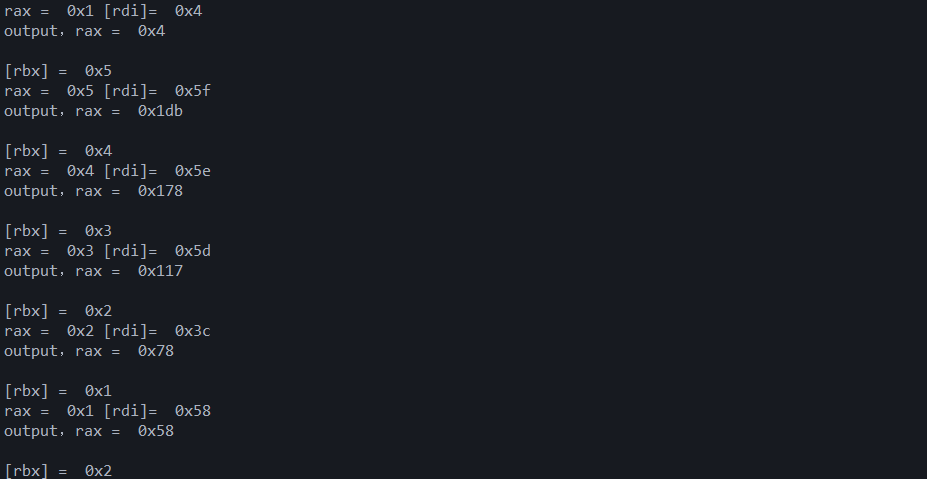
推导
因为密文说16字节的,我们将真正的密文提取出来和我们输入假flag产生的密文也提取出来,进行对比
Python
密文
unsigned int data[16] = {
0x00000436, 0x000002B4, 0x000002AF, 0x00000312, 0x000002EA, 0x00000253,
0x0000020A, 0x0000028E,
0x000001C6, 0x0000015C, 0x0000017C, 0x0000017A, 0x0000069E, 0x000004AE,
0x000004B1, 0x00000522
};
假flag输出的结果密文
unsigned int data[16] = {
0x00000466, 0x000002F9, 0x00000329, 0x0000046E, 0x00000290, 0x00000184,
0x000001E4, 0x0000023A,
0x00000183, 0x000000C1, 0x0000011E, 0x00000122, 0x00000646, 0x00000467,
0x000004F7, 0x000005EA
};
这是根据条件输出得到的规律;
x1*1+x2*5+x3*4+x4*3=0x436
y1*1+y2*5+y3*4+y4*3=0x2B4
z1*1+z2*5+z3*4+z4*3=0x2AF
n1*1+n2*5+n3*4+n4*3=0x312
x1*2+x2*1+x3*2+x4*3=0x2EA
y1*2+y2*1+y3*2+y4*3=0x253
z1*2+z2*1+z3*2+z4*3=0x20A
n1*2+n2*1+n3*2+n4*3=0x28E
x1*2+x2+x3+x4=0x1c6
y1*2+y2+y3+y4=0x15c
z1*2+z2+z3+z4=0x17c
n1*2+n2+n3+n4=0x17a
x1*3+x2*5+x3*4+x4*7=0x69e
y1*3+y2*5+y3*4+y4*7=0x4ae
z1*3+z2*5+z3*4+z4*7=0x4b1
n1*3+n2*5+n3*4+n4*7=0x522

z3解密
解密脚本:
Python
from z3 import *
# 定义变量
x = [Int(f'x{i}') for i in range(1, 5)]
y = [Int(f'y{i}') for i in range(1, 5)]
z = [Int(f'z{i}') for i in range(1, 5)]
n = [Int(f'n{i}') for i in range(1, 5)]
# 定义目标值
goal = [
0x466,
0x2f9,
0x329,
0x46e,
0x290,
0x184,
0x1e4,
0x23a,
0x183,
0xc1,
0x11e,
0x122,
0x646,
0x467,
0x4f7,
0x5ea
]
# 定义约束条件
constraints = [
x[0]*1 + x[1]*5 + x[2]*4 + x[3]*3 == goal[0],
y[0]*1 + y[1]*5 + y[2]*4 + y[3]*3 == goal[1],
z[0]*1 + z[1]*5 + z[2]*4 + z[3]*3 == goal[2],
n[0]*1 + n[1]*5 + n[2]*4 + n[3]*3 == goal[3],
x[0]*2 + x[1]*1 + x[2]*2 + x[3]*3 == goal[4],
y[0]*2 + y[1]*1 + y[2]*2 + y[3]*3 == goal[5],
z[0]*2 + z[1]*1 + z[2]*2 + z[3]*3 == goal[6],
n[0]*2 + n[1]*1 + n[2]*2 + n[3]*3 == goal[7],
x[0]*2 + x[1] + x[2] + x[3] == goal[8],
y[0]*2 + y[1] + y[2] + y[3] == goal[9],
z[0]*2 + z[1] + z[2] + z[3] == goal[10],
n[0]*2 + n[1] + n[2] + n[3] == goal[11],
x[0]*3 + x[1]*5 + x[2]*4 + x[3]*7 == goal[12],
y[0]*3 + y[1]*5 + y[2]*4 + y[3]*7 == goal[13],
z[0]*3 + z[1]*5 + z[2]*4 + z[3]*7 == goal[14],
n[0]*3 + n[1]*5 + n[2]*4 + n[3]*7 == goal[15]
]
# 创建求解器
solver = Solver()
# 添加约束条件
solver.add(constraints)
# 求解
if solver.check() == sat:
model = solver.model()
for i in range(1, 5):
print(f'x{i} = {model[x[i-1]]}')
print(f'y{i} = {model[y[i-1]]}')
print(f'z{i} = {model[z[i-1]]}')
print(f'n{i} = {model[n[i-1]]}')
else:
print('无解')
得到的结果,将其按照数组来填充

得到
Python
这是真flag解密后的结果:
x1 = 100
y1 = 89
z1 = 119
n1 = 92
x2 = 66
y2 = 5
z2 = 69
n2 = 4
x3 = 84
y3 = 83
z3 = 4
n3 = 104
x4 = 104
y4 = 82
z4 = 69
n4 = 86
100,89,119,92,66,5,69,4,84,83,4,104,104,82,69,86
这是假flag解密后的结果:
x1 = 60
y1 = 1
z1 = 47
n1 = 4
x2 = 88
y2 = 87
z2 = 86
n2 = 95
x3 = 89
y3 = 13
z3 = 14
n3 = 94
x4 = 90
y4 = 91
z4 = 92
n4 = 93
60,1,47,4,88,87,86,95,89,13,14,94,90,91,92,93
按照我的思路来填充结果数组;
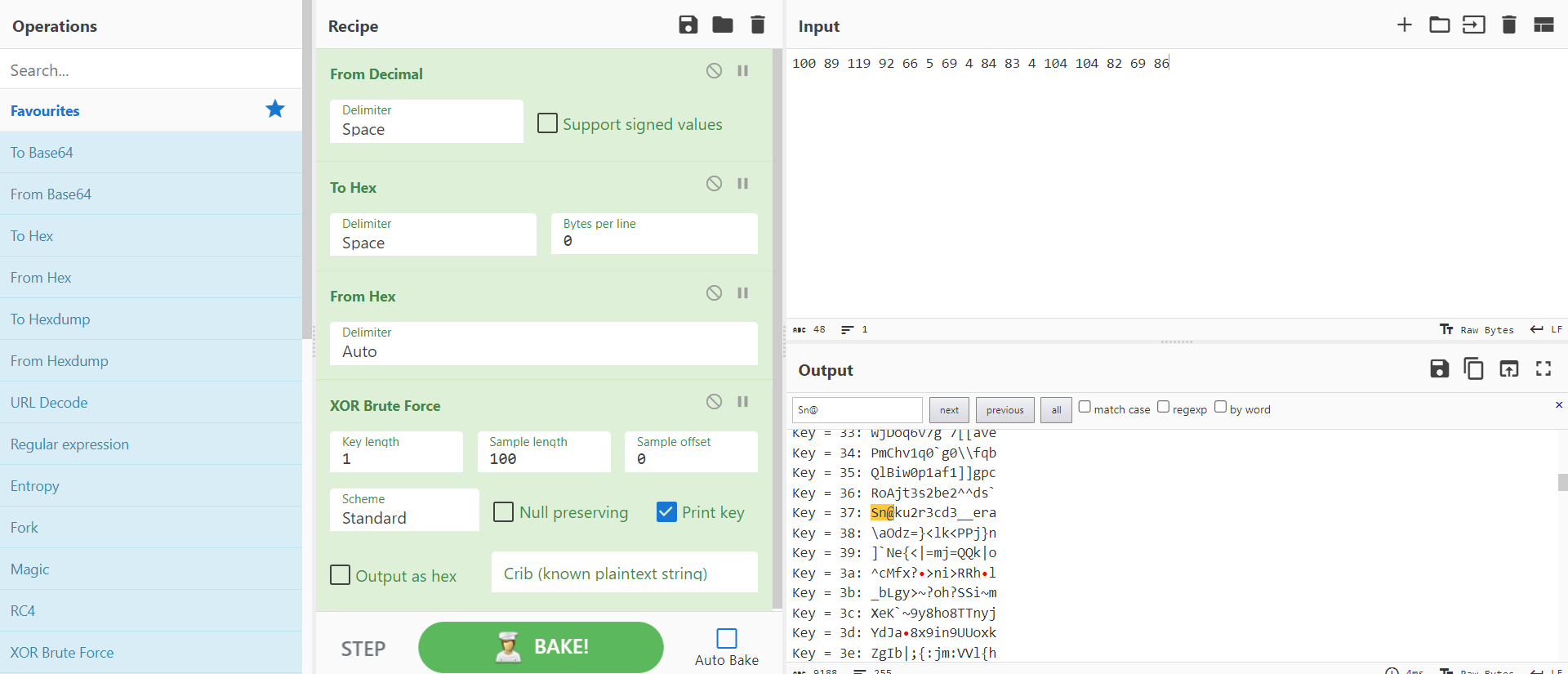
因为刚才说了,异或的值不清楚,但是一直为单字节固定值,所以使用Cybe的爆破功能。
根据程序的验证功能可知,flag以Sn@K开头,所以找到了真正的flag
但是顺序发生了变化,下面是假flag生成密文解密之后的结果,发现密文变化了
±----------------------------------------------------------------------+
| Sn@ku2r3cd3__era |
| Sn@k78906ba15432 |
| |
| Sn@k0123456789ab |
| |
| 经过交换后的结果: |
| |
| Sn@k78906ba15432 |
| |
| 按照我们构造的flag交换顺序后的字符串来恢复 |
| 恢复 |
| Sn@k3_are_cu2r3 |
±----------------------------------------------------------------------+
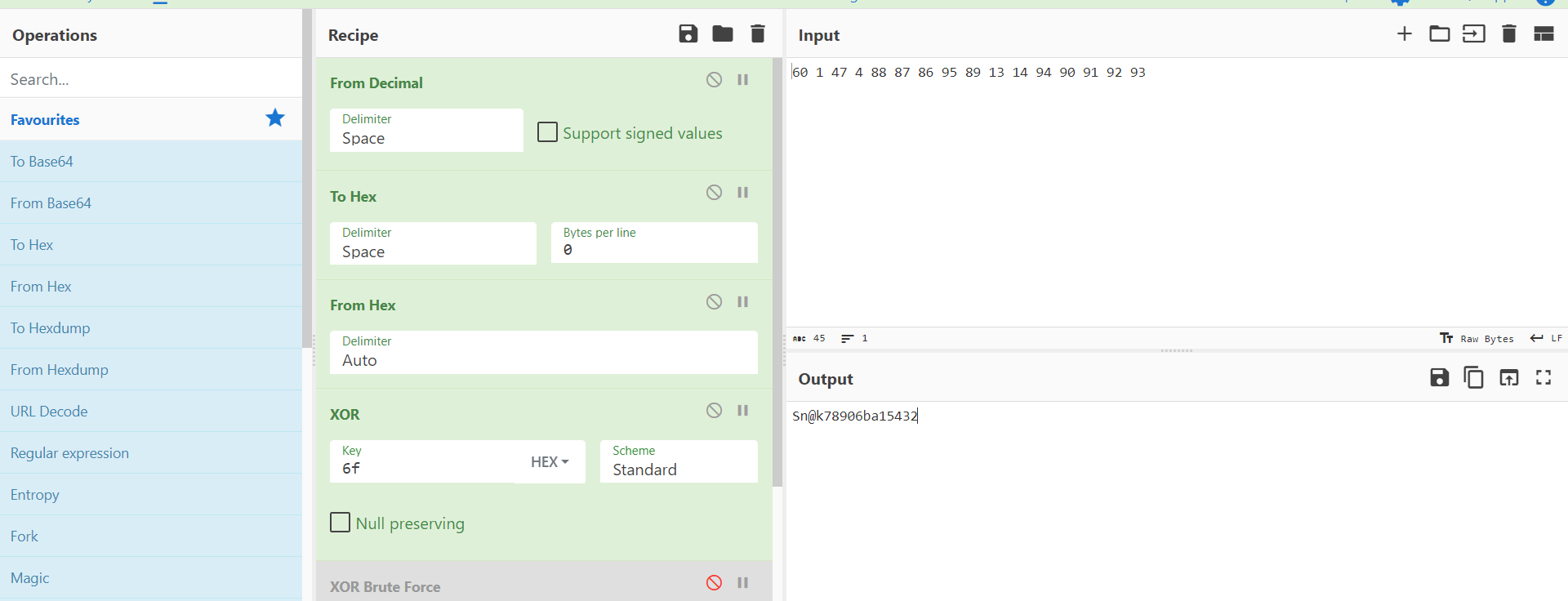
成功验证!