前言
本篇文章为博主进行代码随想录——数组练习后的总结会涉及到每一道题目的详细的思路整理,以及本人的易错点,希望对大家有所帮助
数组介绍:
数组在C语言中就已经有所涉及,它是一个最基础的数据结构,而在数据结构中,通常它属于线性表中的顺序表(Sequence List),它是一种特殊的线性存储结构。
特点:
逻辑上相邻的数据元素,在物理次序上也是相邻的。——也就是说它们挨着存储
任意元素都可在相同的时间内存取,即顺序存储的数组是一个随即存取结构
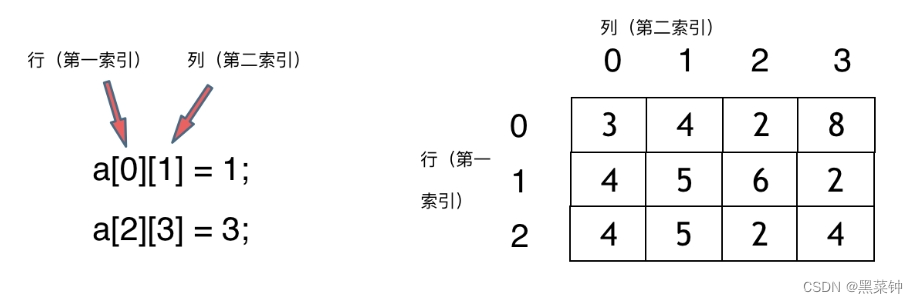
顺序存储:行优先和列优先两种顺序
行优先——每一行的第一个元素位于低地址,最后的位于高地址,且连续
列优先——每一行的第一个元素位于低地址,最后的位于高地址,且连续
优点:
它访问速度快,但是无法高效插入和删除元素
数组理论基础
数组是存放在连续内存空间上的相同类型数据的集合
数组的元素是不能删的,只能覆盖
如果使用C++的话,要注意vector 和 array的区别,vector的底层实现是array,严格来讲vector是容器,不是数组。
对于二维数组来说——它的顺序是否连续呢——语言不同,会造成一定的差异,而c++中的二维数组是连续的,Java却不是这样存储的。
二分查找
题目:. - 力扣(LeetCode)
方法——使用二分查找的方式
注意——
1.要看清题目是否给出有序数组,这是一个二分查找的条件
2.循环不变量的思想——区间设置到底是左闭右开还是左闭右闭
第一次写可能出现的问题——
1.if中的==而不是=
2.left和right是数组的位置标号,而非数组内容
3.要注意从开始就考虑是选取左闭右闭还是左闭右开
4.注意函数最后要在while循环外有一个return 否则错误
二分查找的方法介绍:
二分法就是设置两个指针,让它们一个在最左边,一个在最右边,而且要设置一个中间值然后为了查找有序数组中的值,不断细分这个数组——假如你要寻找的这个数是小于中间值的,那么这个数就在左边,这时候我们只需要在左边再次重复操作——直到左边指针和右边指针找到了那个数(这个结束的条件有两种情况)
那这样写第一遍你会发现——可能还是会发生错误——
在while循环中,结束的条件到底是left<right还是left<=right呢?
在循环中找到要继续查找的是左边或右边后,right或left是等于middle(中间值)呢,还是其他呢?
那么接下来就介绍一个概念——循环不变量
在整个过程中我们这个数组在查找时,是把它看成左闭右闭还是左闭右开呢?这个需要你在循环之前需要搞清楚的量,就是所谓的循环不变量
当左闭右闭时——
- 1.while括号里的条件为——left<=right因为这时left=right对于闭区间来说,是成立的
- 2.而当需要移动指针时,right或者是left是直接等于middle-1/middle+1的,因为已经判断好了middle上不是需要找的数.
当左闭右开时——
- 1.while括号里的条件为——left<right因为这时left=right对于半开区间来说,是不成立的
- 2.而当需要移动指针时,right是直接等于middle的,因为这时候right是一个开区间,只有放在已查看过的middle,才不至于略掉其他的可能为你要寻找的数
学会之后:第二次可能写出现的问题——
对于左闭右开的形式,从一开始就需要做出改变
——
1.定义时,右边的要定义的比左闭右闭多一位
2.对于左边的变到中间,是中间+1,因为这里是闭区间
3.对于右边的变到中间,就是中间了
- 更多有关二分查找的题(也来自代码随想录)
- 35.搜索插入位置(opens new window)
- 34.在排序数组中查找元素的第一个和最后一个位置(opens new window)
- 69.x 的平方根(opens new window)
- 367.有效的完全平方数(opens new window)
这里只记录一个二分查找扩展——搜索插入位置
暴力解法
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
for (int i = 0; i < nums.size(); i++) {
// 分别处理如下三种情况
// 目标值在数组所有元素之前
// 目标值等于数组中某一个元素
// 目标值插入数组中的位置
if (nums[i] >= target) { // 一旦发现大于或者等于target的num[i],那么i就是我们要的结果
return i;
}
}
// 目标值在数组所有元素之后的情况
return nums.size(); // 如果target是最大的,或者 nums为空,则返回nums的长度
}
};二分法(这里采用c++其中的vector<int>& nums相当于C语言中传入一个整型数组nums,nums.size()返回这个数组的大小)
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
int left = 0;
int right = n; // 定义target在左闭右开的区间里,[left, right) target
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在 [middle+1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值的情况,直接返回下标
}
}
// 分别处理如下四种情况
// 目标值在数组所有元素之前 [0,0)
// 目标值等于数组中某一个元素 return middle
// 目标值插入数组中的位置 [left, right) ,return right 即可
// 目标值在数组所有元素之后的情况 [left, right),因为是右开区间,所以 return right
return right;
}
};
移除元素
题目:. - 力扣(LeetCode)

第一遍练习会出现的问题——
对于i不知道如何让它再次看之前的数值——i--即可
第二次循环时,需要覆盖,这时候要设置j=i+1,n[j]=n[j-1]
方法一——暴力解题法
对于移除元素,在循环中找到所满足条件的数组元素,然后覆盖其位置数值(用循环)……
方法二——快慢指针法
首先来介绍一下什么是快指针和慢指针:



具体方法思路——
首先假设数组为[3,2,2,3]需要去除的值是3
快慢指针初始均指向第一个数,慢指针是为了获取最终数组,它这个位置假如遇到需要去除的值,则要覆盖——快指针获取这个覆盖的值,即最后把所有的需要去除的数给去除。
所以循环是现判断快指针指向的位置是否为需要去除的值——是则往下移一位,不是则把这个值赋给慢指针所指向的值,然后慢指针往后移,循环往复,直到快指针遍历结束
例子:假如第一个遇到的就是需要去除的值,那么快指针会先往下一步,然后如果所指向的值不为去除的值——赋值给慢指针,这样可以覆盖掉第一个需要去除的值,然后慢指针往后一步,如果慢指针还是指向需要去除的值,则重复上述步骤,这样直到最后,快指针可以把所有的不需要去除的值给按顺序覆盖到需要去除的地方——完成代码即可
int removeElement(int* nums, int numsSize, int val) {
int s=0;
int q=0;
for(;q<numsSize;q++)
{
if(nums[q]!=val)
{
nums[s]=nums[q];
s++;
}
}
return s;
}注意写代码时——这里的快慢指针不是真的指针,而是设置的数组下标。
有序数组的平方
题目:. - 力扣(LeetCode)

第一次暴力解题会出现的问题——
1.平方的for循环要i从0——numsSize(<号的时候)
2.排序方式——这里用选择排序示例:
for(int i=0;i<numsSize-1;i++)
{
for(int j=i+1;j<numsSize;j++)
{
if(nums[i]>nums[j])
{
int t=nums[i];
nums[i]=nums[j];
nums[j]=t;
}
}
}第二次用双指针写出现的问题——
1.新建的数组需要动态开辟空间?
双指针法
设计思路:
首先先观察题目——发现如果平方之后,最大值一定是最左边或是最右边的平方,而且是按一定顺序排列的数组,如果是右边的平方大,则下一个就是左边的平方,然后再往里比较,因此这里借助两个指针,一左一右,进行大小比较,然后把大的一个赋值给新数组
双指针法的具体思路:
首先先创造一个新数组——和原来的数组一样大小,这里使用动态数组的方式,然后设置两个int类型的数据,它们分别为0和数组大小-1,然后比较这两个所指的原数组数据平方谁大——谁就把这个放进新数组的最右边,然后这个指针往中间的方向移动——再次比较——再次赋值给新数组的“指针”……直到两个指针相遇,即可结束循环——代码也就完成了
代码:(result是新数组)
class Solution {
public:
vector<int> sortedSquares(vector<int>& A) {
int k = A.size() - 1;
vector<int> result(A.size(), 0);
for (int i = 0, j = A.size() - 1; i <= j;) {
if (A[i] * A[i] < A[j] * A[j]) {
result[k--] = A[j] * A[j];
j--;
}
else {
result[k--] = A[i] * A[i];
i++;
}
}
return result;
}
};长度最小的子数组
题目:
. - 力扣(LeetCode)

第一次写出现的问题——
1.没有思路
2.返回值?
3.这个int类型的最大值不知道是怎么写?
INT32_MAX这里的思路其实看过代码之后就有点恍然大悟了,但是不知道怎么想的,很妙
这道题依然采用两个指针的方法——不过这里方法叫滑动窗口,因为可能指针的移动像滑动吧🤭
1.由于返回的是长度最小的满足情况的数组大小——因此我们先把这个长度设置为最大——也就是int的最大,用INT32_MAX来表示,如果最后结果仍未这个值,说明没有满足条件的情况,返回0,否则返回长度的最小值。
2.这里使用双指针的原因是——整个数组的满足范围不限制,而其中的每一组组合都可能满足,如果想要简便的实现的话,需要两个指针,它们不断变换,我们求其中的总值,如果满足情况,则赋值给返回值,最后不断更新返回值的较小值,就可找到返回值最小的情况,题目也就满足了
滑动窗口的代码实现:

这里两个分别是指针1和指针2(刚开始都在同一位置),需要之间的值大于7,先设置一个sum的初始值为0,进入循环中,加上n[j],如果这时候的sum>=7,则直接给result赋值1,如果不是——指针j往下移动,然后循环内又再加上n[j]……直到指针指向第二个2时,sum>=7了,则先赋值给result一个较小值,然后指针1开始移动——寻找这个满足条件的区间内可以有更小的可能吗?(这时候需要减去n[i]后移动这个指针),然后发现从3——2区间也成立,然后再循环,直到指针循环到最后,result自然=最小值
代码:
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX;
int sum = 0; // 滑动窗口数值之和
int i = 0; // 滑动窗口起始位置
int subLength = 0; // 滑动窗口的长度
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
// 注意这里使用while,每次更新 起始位置,并不断比较子序列是否符合条件
while (sum >= s) {
subLength = (j - i + 1); // 取子序列的长度
result = result < subLength ? result : subLength;
sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处,不断变更i(子序列的起始位置)
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}这个时间复杂度为O(n)——这个是看每一个元素被操作的次数,因为有两个指针,每个元素在滑动窗进来一次出去一次,时间复杂度为2n——O(n)
螺旋矩阵
题目:59. 螺旋矩阵 II - 力扣(LeetCode)
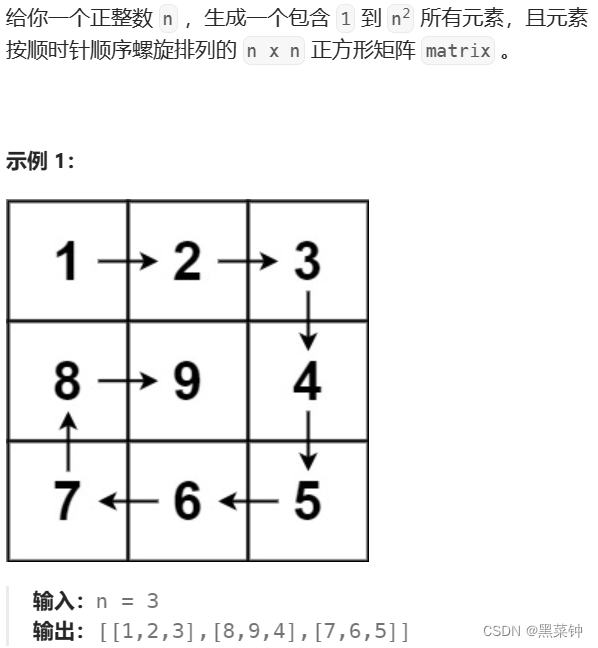
这个和二分法一样,需要有不变量——左闭右开,
而这里发生错误的地方在于——
1.要知道每一个矩阵需要绕的圈数——n/2,
2.注意一圈过后,它的起始位置发生改变,要都加1
3.如果n为奇数的话,最后要判断一下,单独把中间的值赋值
⭐注意如何在c语言中动态初始化二维数组:
int** generateMatrix(int n, int* returnSize, int** returnColumnSizes){
//初始化返回的结果数组的大小
*returnSize = n;
*returnColumnSizes = (int*)malloc(sizeof(int) * n);
//初始化返回结果数组ans
int** ans = (int**)malloc(sizeof(int*) * n);
}复习——malloc和free
free参数要么是NULL要么是之前从malloc、calloc、realloc返回的值,无返回值
malloc返回一块连续的数组,返回类型为void*,C和C++规定,void*类型可以强制转换为任何其他类型的指针
而malloc里面放的是需要空间的大小,一般用sizeof来计算
注意:
要检查所请求的内存是否分配成功
必须要释放
可以使用exit(1)——用于退出整个程序,终止进程,返回1代表异常终止,返回0正常退出
方法——模拟行为,这里重要的就是考虑循环不变量,而除此之外其它的也很重要——其中的思想,模拟过程
这其实是一个二维数组的初始化,不过更为复杂,这里看代码——
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
int loop = n / 2; // 每个圈循环几次,例如n为奇数3,那么loop = 1 只是循环一圈,矩阵中间的值需要单独处理
int mid = n / 2; // 矩阵中间的位置,例如:n为3, 中间的位置就是(1,1),n为5,中间位置为(2, 2)
int count = 1; // 用来给矩阵中每一个空格赋值
int offset = 1; // 需要控制每一条边遍历的长度,每次循环右边界收缩一位
int i,j;
while (loop --) {
i = startx;
j = starty;
// 下面开始的四个for就是模拟转了一圈
// 模拟填充上行从左到右(左闭右开)
for (j = starty; j < n - offset; j++) {
res[startx][j] = count++;
}
// 模拟填充右列从上到下(左闭右开)
for (i = startx; i < n - offset; i++) {
res[i][j] = count++;
}
// 模拟填充下行从右到左(左闭右开)
for (; j > starty; j--) {
res[i][j] = count++;
}
// 模拟填充左列从下到上(左闭右开)
for (; i > startx; i--) {
res[i][j] = count++;
}
// 第二圈开始的时候,起始位置要各自加1, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)
startx++;
starty++;
// offset 控制每一圈里每一条边遍历的长度
offset += 1;
}
// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
if (n % 2) {
res[mid][mid] = count;
}
return res;
}
};- 时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
- 空间复杂度 O(1)
总结
这里的数组题目公涉及了三种方法——
二分法:注意循环不变量
双指针法:通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
滑动窗口:滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)
最好的方法是多用多看多练,而且要及时总结错误及思路。
感谢观看完毕,欢迎点赞收藏😉