二分通用模板+例题java

news2025/1/12 6:04:14

🧡🧡二分大前提🧡🧡

有序数列！！

🧡🧡模板🧡🧡

查找具体某个元素

while(left<=right) ：三个分支，在循环里直接返回答案

//二分查找具体元素
public int search(int[] nums,int target) {
	int left=0;
	int right=nums.length-1;
	while(left<=right) {
		int mid=(left+right)>>>1; 
		if(nums[mid]==target) {
			return mid;
		}else if(nums[mid]>target) {
			right=mid-1;
		}else {
			left=mid+1;
		}
	}
	return -1;
}

查找满足条件的最小/最大元素

while(left<right) ：两个分支，答案需要退出循环再做进一步处理

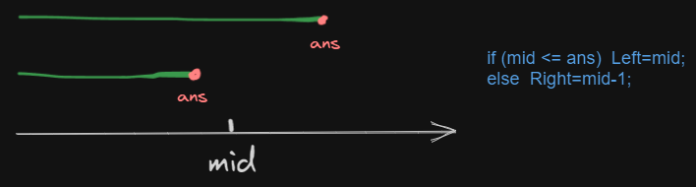
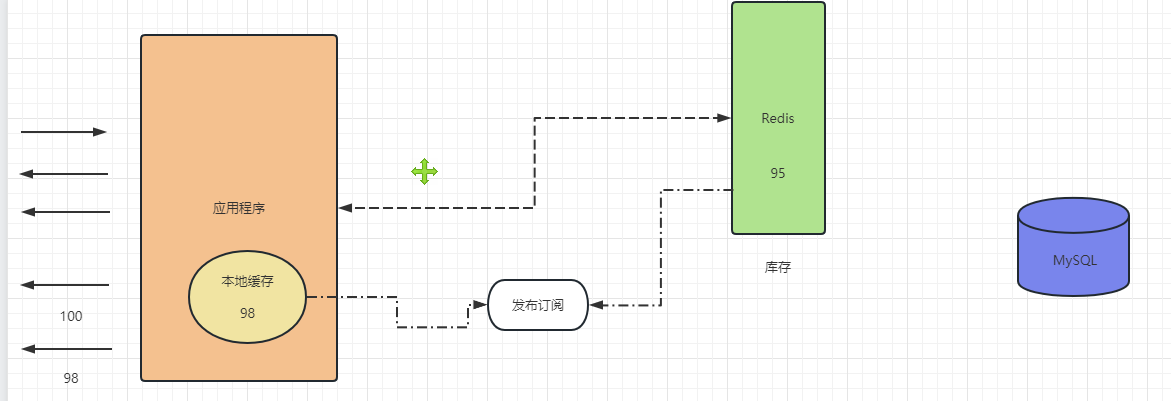
如下图，绿色为符合条件的区间，我们需要找到满足“最小性”的ans。画了两条绿线代表mid与ans位置相对大小的两种情况。

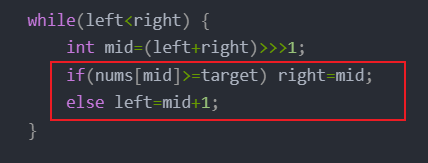
//找到第一个大于等于target的位置
//即找到00000111111中第一个1的位置
public int func(int[] nums, int target) {	  
	int left=0;
	int right=nums.length-1;
	  
	while(left<right) {
		int mid=(left+right)>>>1;
		if(nums[mid]>=target) right=mid;
		else left=mid+1;
	}
	  
	//循环退出，left==right
	return left;
}

同理，如下图，绿色为符合条件的区间，我们需要找到满足“最大性”的ans

//找到第一个小于等于target的位置
//即找到11111100000中最后一个1的位置
public int func(int[] nums, int target) {	  
	int left=0;
	int right=nums.length-1;
	  
	while(left<right) {
		int mid=(left+right+1)>>>1; //注意+1
		if(nums[mid]<=target) left=mid;
		else right=mid-1;
	}
	
	//循环退出，left==right
	return left;
}

注意点

以上代码中，(left+right)>>>1 等价于 (left+right)/2，其原理是进无符号右移，例如1100>>>1 变为 0110。有些情况下，为避免left+right爆范围（如果left和right都是int型，那么它们相加超过65535就会爆范围，产生小错误），可以采用变式：left + (right-left)>>>1，这样爆范围的风险就小了。
如何确保if else中的条件顺序不乱，笔者是这样记忆的：先写if的条件，找“最小性”，则需要mid >= xxx （>=就有“最小”的意思咯）；找“最大性”，则需要 mid <= xxx ( <=就有“最大”的意思咯）。然后接着写else即可。

对于(left+right)>>>1 和 (left+right+1)>>>1 的区别为“是否+1”，为避免混淆两种最大最小性的二分查找代码，笔者是这样记忆的：若二分代码中有mid-1，则对left+right进行填补+1；若二分代码中有mid+1，则不进行填补+1。（有负则补）

🧡🧡例题🧡🧡

力扣704-二分查找

public class Solution {
    public int search(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        while(left<=right) {   
            int mid=(right-left)/>>>1+left; //为什么不是直接(right+left)/2呢？
            if(nums[mid]==target) {
                return mid;
            }else if(nums[mid]>target) {
                right=mid-1;
            }else {
                left=mid+1;
            }
        }
        return -1;
    }
}

acwing-789数的范围

import java.util.Scanner;

public class Main{
	public static int n, q;
	public static int[] arr;

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt();
		q = sc.nextInt();
		sc.nextLine(); // 消耗掉输入中的换行符

		arr = new int[n + 1];

		// input arr
		String inputString = sc.nextLine();
		String[] inputCharArr = inputString.split(" ");

		for (int i = 0; i < n; i++) {
			arr[i] = Integer.parseInt(inputCharArr[i]);
		}
//		System.out.println(Arrays.toString(arr));

		while (q-- > 0) {
			int x = sc.nextInt();
			int left = 0, right = n - 1;
			while (left < right) {
				int mid = (left + right) >>> 1; // 除2，向下取整
				if (arr[mid] >= x)
					right = mid;
				else
					left = mid + 1;
			}
			if (arr[left] == x) {
				System.out.print(left + " ");

				right = n - 1;
				while (left < right) {
					int mid = (left + right + 1) >>> 1; // 除2，向上取整
					if (arr[mid] <= x)
						left = mid;
					else
						right = mid - 1;
				}
				System.out.println(right);
			} else {
				System.out.println("-1 -1");
			}
		}
	}
}

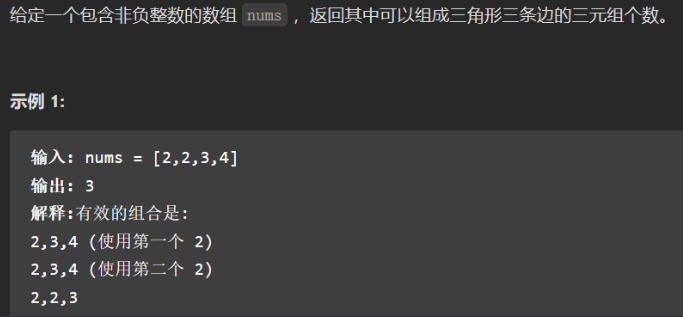
力扣611-有效三角形的个数

思路：

三层for循环暴力枚举三条边，统计个数， $O（N^3）$
二层for循环枚举前两条边，再套一个二分找出能最大满足的边的下标，即可求出个数 $O（N^2logN）$

//排序+二分
public int triangleNumber(int[] nums) {
	int len=nums.length;
	//排序
	Arrays.sort(nums);
	if(len<3) return 0;
	int ans=0;
	for(int a=0;a<len-2;a++) {
		for(int b=a+1;b<len-1;b++) {
			if(nums[a]+nums[b]<=nums[b+1]) continue; 
			int left=b+1,right=len-1;
			//模板：找满足条件的最后一个（最大性）
			while(left<right) {
				int mid=(left+right+1)>>>1;
				if(nums[mid]>=nums[a]+nums[b]) {
					right=mid-1;
				}else {
					left=mid;
				}
			}
			ans+=left-b;
		}
	}
	return ans;
}