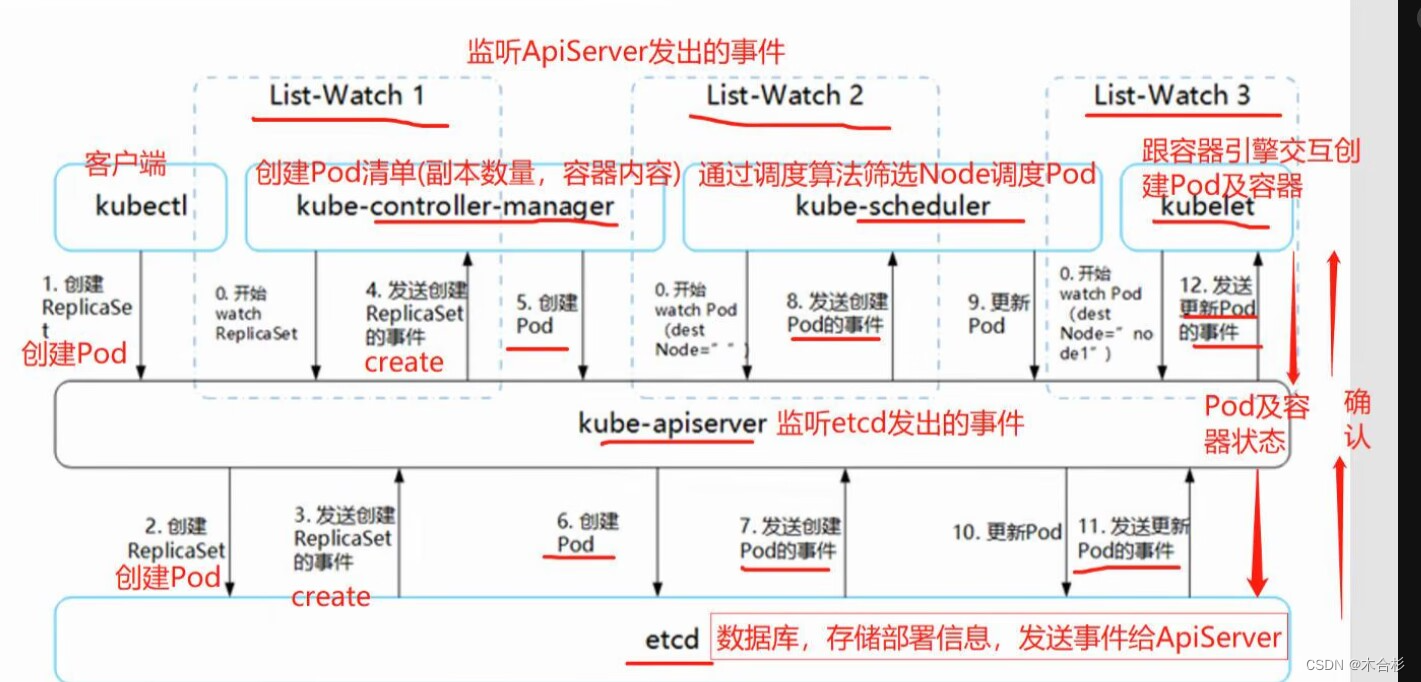
概率基础——多元正态分布
介绍
多元正态分布是统计学中一种重要的多维概率分布,描述了多个随机变量的联合分布。在多元正态分布中,每个随机变量都服从正态分布,且不同随机变量之间可能存在相关性。本文将以二元标准正态分布为例,介绍多元正态分布的理论和公式。
理论及公式
对于二元标准正态分布,假设随机变量 X X X和 Y Y Y都服从均值为0,方差为1的标准正态分布,并且随机变量 X X X和 Y Y Y之间的协方差为0。这意味着 X X X和 Y Y Y是相互独立的。其概率密度函数(PDF)为:
f ( x , y ) = 1 2 π e − x 2 + y 2 2 f(x,y) = \frac{1}{2\pi} e^{-\frac{x^2+y^2}{2}} f(x,y)=2π1e−2x2+y2
其中, ( x , y ) (x, y) (x,y)表示二维平面上的一个点, π \pi π是圆周率。
对于 n n n 元标准正态分布,如果向量 Z Z Z由若干个遵从标准正态分布的独立通分布随机变量 Z 1 , Z 2 , … , Z n Z_1, Z_2, \ldots, Z_n Z1,Z2,…,Zn组成,则向量 Z Z Z服从 n n n 元标准正态分布。
参数说明
在二元标准正态分布中,参数已经确定为均值为0,方差为1,并且协方差为0。这意味着随机变量 X X X和 Y Y Y之间不存在线性相关性,即它们是相互独立的。这些参数的设置使得二元标准正态分布的形状符合常见的二维高斯分布的特征。
Python实现
下面是使用Python绘制二元标准正态分布的示例代码:
import numpy as np
import matplotlib.pyplot as plt
mean = np.array([0, 0])
conv = np.array([[1, 0], [0, 1]])
x, y = np.random.multivariate_normal(mean, conv, size=5000).T
plt.figure(figsize=(10, 10))
plt.plot(x, y, 'bo', alpha=0.5)
plt.gca().axes.set_xlim(-4, 4)
plt.gca().axes.set_ylim(-4, 4)
plt.grid(ls='--')
plt.show()
在代码中,生成了均值为0,方差为1,随机变量间协方差为0的二元正态分布,随机变量X和Y,
一共生成了5000组样本,结果如图所示。

从图中可以发现,在均值点(此处对应原点)附近,样本出现的概率较高,远离均值点的地方样本出现的概率较低(此处设置的样本点透明度为0.2,颜色越深表示样本点个数越多),在中心附近概率密度最高,随着离中心点的距离增加,概率密度逐渐减小。
import numpy as np
import matplotlib.pyplot as plt
mean = np.array([0, 0])
conv_1 = np.array([[1, 0], [0, 1]])
conv_2 = np.array([[4, 0], [0, 0.25]])
x_1, y_1 = np.random.multivariate_normal(mean, conv_1, size=5000).T
x_2, y_2 = np.random.multivariate_normal(mean, conv_2, size=5000).T
plt.figure(figsize=(10, 10))
plt.plot(x_1, y_1, 'bo', alpha=0.05)
plt.plot(x_2, y_2, 'ro', alpha=0.05)
plt.gca().axes.set_xlim(-6, 6)
plt.gca().axes.set_ylim(-6, 6)
plt.grid(ls='--')
plt.show()
通过调整参数,可以逐渐将二元正态分布变换为二元一般正态分布,可以调整的参数主要由3个方面:
- 调整多个随机变量自身的均值,让样本整体在二维平面上进行平移;
- 调整随机变量X和Y的方差,当然此时还是保留它们互相之间彼此独立的关系,以下先观察一下样本图像的特点。
与标准正态分布对照,

- 保持随机变量的方差不变,通过改变协方差的值,来观察协方差的变换给随机变量间的相关特性带来的影响以及图像上的变换。
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(2, 2, figsize=(10, 5))
mean = np.array([0, 0])
conv_1 = np.array([[1, 0], [0, 1]])
conv_2 = np.array([[1, 0.3], [0.3, 1]])
conv_3 = np.array([[1, 0.85], [0.85, 1]])
conv_4 = np.array([[1, -0.85], [-0.85, 1]])
x_1, y_1 = np.random.multivariate_normal(mean, conv_1, size=5000).T
x_2, y_2 = np.random.multivariate_normal(mean, conv_2, size=5000).T
x_3, y_3 = np.random.multivariate_normal(mean, conv_3, size=5000).T
x_4, y_4 = np.random.multivariate_normal(mean, conv_4, size=5000).T
ax[0][0].plot(x_1, y_1, 'bo', alpha=0.5)
ax[0][1].plot(x_2, y_2, 'bo', alpha=0.5)
ax[1][0].plot(x_3, y_3, 'bo', alpha=0.5)
ax[1][1].plot(x_4, y_4, 'bo', alpha=0.5)
ax[0][0].grid(ls='--')
ax[0][1].grid(ls='--')
ax[1][0].grid(ls='--')
ax[1][1].grid(ls='--')
plt.show()

在代码中,生成了4组二元正态分布,其中第一组是作为对比的二元标准正态分布,第二组的协方差为0.3,第三组的协方差为0.85,第四组的协方差为-0.85。
与二元标准正态分布呈圆形相比,协方差不为0的二元正态分布呈现一定斜率的椭圆,且协方差越大,椭圆越窄;协方差为正和为负,椭圆的方向是相反的,对应于随机变量之间的正相关和负相关。
总结
本文介绍了多元正态分布及Python实现,叙述了每个随机变量都服从正态分布,且不同随机变量之间可能存在相关性的多元正态分布理论,并通过调整参数,将二元正态分布变换为二元一般正态分布。