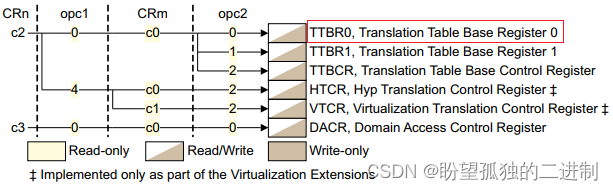
目录
一、介绍
二、方法论
三、应用
四、优势
五、局限性
六、代码
七、结论
一、介绍
反距离加权 (IDW) 是一种广泛用于地理信息系统 (GIS) 和环境科学的空间插值技术,用于根据附近位置的值估计任何位置的缺失值。它的基本原理是直观的:离兴趣点近的位置比离目标点远的位置更相似。本文深入探讨了 IDW 的方法、应用、优势和局限性,并深入了解了其在空间分析中的重要性。
无论近在咫尺,每一点都在讲述一个故事。通过反距离加权的视角,每个位置都在空间分析的合唱中找到了自己的声音。
二、方法论
IDW 基于以下概念,即给定位置的插值是周围位置已知值的加权平均值。根据指定的数学函数,权重随着从已知点到未知点的距离的增加而减小。通常,权重 (w) 使用公式 wi=1/dip 计算,其中 di 是已知点 i 与需要估计的点之间的距离,p 是一个功率参数,用于确定权重随距离下降的速度。p的选择至关重要;值越大,对最近邻的影响越大,而值越低,影响在周围点之间分布得更均匀。
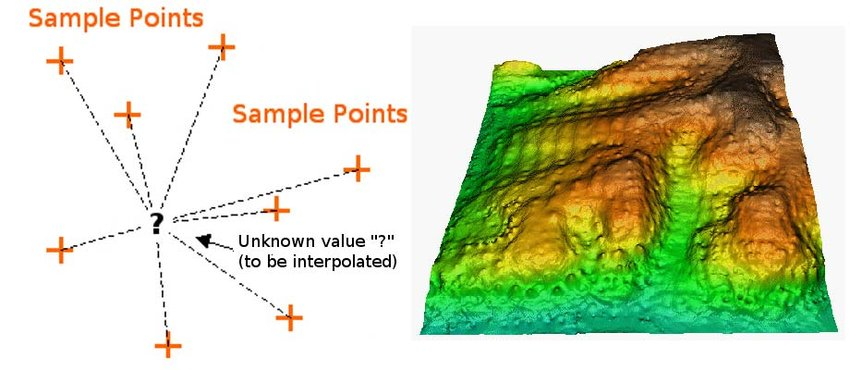
然后使用公式 z^=∑i=1n(wi⋅zi)/∑i=1nwi 计算未知位置的估计值 (z^),其中 zi 是第 i个位置的已知值。此公式确保每个已知值对插值的影响与其与估计点的距离成反比。
三、应用
IDW 用途广泛,可在分析空间数据的各个领域找到应用。在环境科学中,它用于插值不同地理区域的降雨量、污染水平、温度和湿度的数据点,从分散的观测中提供全面的空间分布图。城市规划者和地理学家使用 IDW 来估计人口密度、土地利用模式和跨城市服务的可及性。在农业中,它有助于绘制土壤特性、水分含量和作物产量图,从而实现精确的农业实践。
四、优势
IDW 的简单性和直观性是其主要优势之一。它不需要对数据进行复杂的数学或统计假设,因此在地质统计学方面专业知识有限的用户可以访问这些数据。该方法非常灵活,允许用户调整功效参数 (p) 以适应其数据的特定性质和他们观察到的空间关系。此外,IDW可以很容易地在大多数GIS软件中实现,从而促进其在各种应用中的广泛使用。
五、局限性
尽管有其优点,但 IDW 也有局限性。一个显著的缺点是其局部插值方法,可能无法准确捕捉全球空间趋势,特别是在地形变化很大或值的现象在空间上突然变化的地区。功率参数 (p) 的选择有些主观,可能会显著影响插值结果,如果不仔细选择,可能会引入偏差。此外,IDW假设各向同性,这意味着它在各个方向上都对距离进行相同的处理,这可能不适用于所有空间现象。
六、代码
为了在 Python 中使用合成数据集来说明反距离加权 (IDW) 插值方法,我们将按照以下步骤操作:
- 生成具有已知值的空间点的合成数据集。
- 实现 IDW 算法。
- 使用实现的 IDW 在覆盖数据集空间范围的网格上插值。
- 绘制原始点和插值曲面以进行可视化。
让我们从创建一个合成数据集开始:
import numpy as np
import matplotlib.pyplot as plt
# Generate synthetic dataset
np.random.seed(42) # For reproducibility
n_points = 100
x = np.random.uniform(0, 10, n_points)
y = np.random.uniform(0, 10, n_points)
values = np.sin(x) + np.cos(y) # Synthetic values
# Plot synthetic dataset
plt.scatter(x, y, c=values, cmap='viridis')
plt.colorbar(label='Value')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Synthetic Dataset')
plt.show()接下来,我们将实现 IDW 算法:
def idw_interpolation(x, y, values, grid_x, grid_y, power=2):
"""
Perform IDW interpolation.
:param x: x coordinates of data points
:param y: y coordinates of data points
:param values: values at the data points
:param grid_x: x coordinates of grid points
:param grid_y: y coordinates of grid points
:param power: power parameter for IDW
:return: interpolated values on the grid
"""
interpolated_values = np.zeros_like(grid_x)
for i in range(grid_x.shape[0]):
for j in range(grid_x.shape[1]):
# Calculate distances between grid point and all data points
distances = np.sqrt((grid_x[i, j] - x)**2 + (grid_y[i, j] - y)**2)
# Avoid division by zero for points exactly at data locations
distances[distances == 0] = 1e-10
# Calculate weights
weights = 1 / distances**power
# Calculate interpolated value
interpolated_values[i, j] = np.sum(weights * values) / np.sum(weights)
return interpolated_values现在,我们将使用此 IDW 函数在网格上进行插值:
# 创建网格
grid_x, grid_y = np.mgrid[0:10:100 j, 0:10:100 j] # 100j 指定 100x100 网格
# 使用 IDW
插值 interpolated_values = idw_interpolation(x, y, values, grid_x, grid_y)
# 绘制
plt.figure(figsize=(10,8))
plt.imshow(interpolated_values, extent=(0, 10, 0, 10), origin='lower', cmap='viridis')plt.scatter(x, y, c='red', label='Data Points') # 叠加原始点
plt.colorbar(label='插值')plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.title('IDW 合成数据集插值')plt.show()此代码将生成两个图:一个显示合成数据集,另一个显示基于 IDW 方法的插值表面,并将原始点叠加进行比较。让我们继续在 Python 环境中执行此操作。
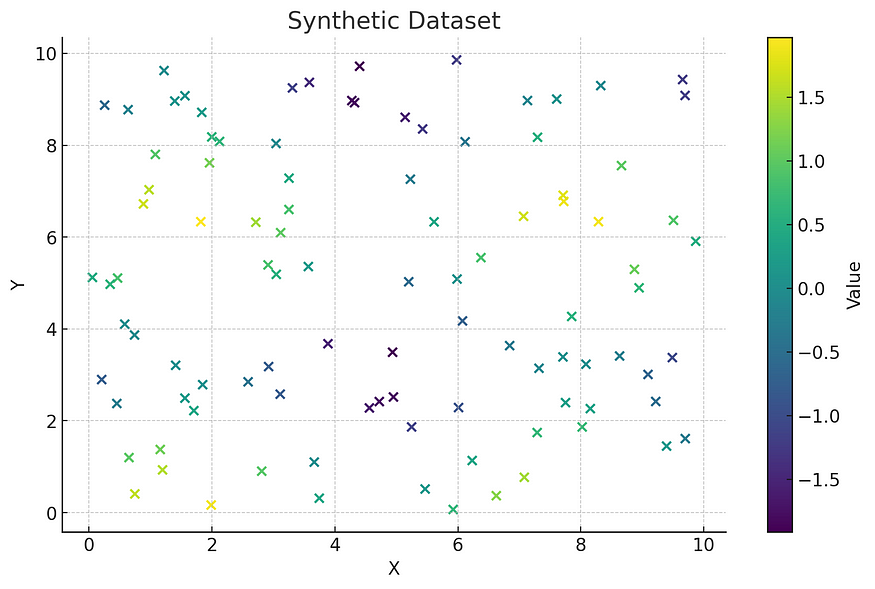
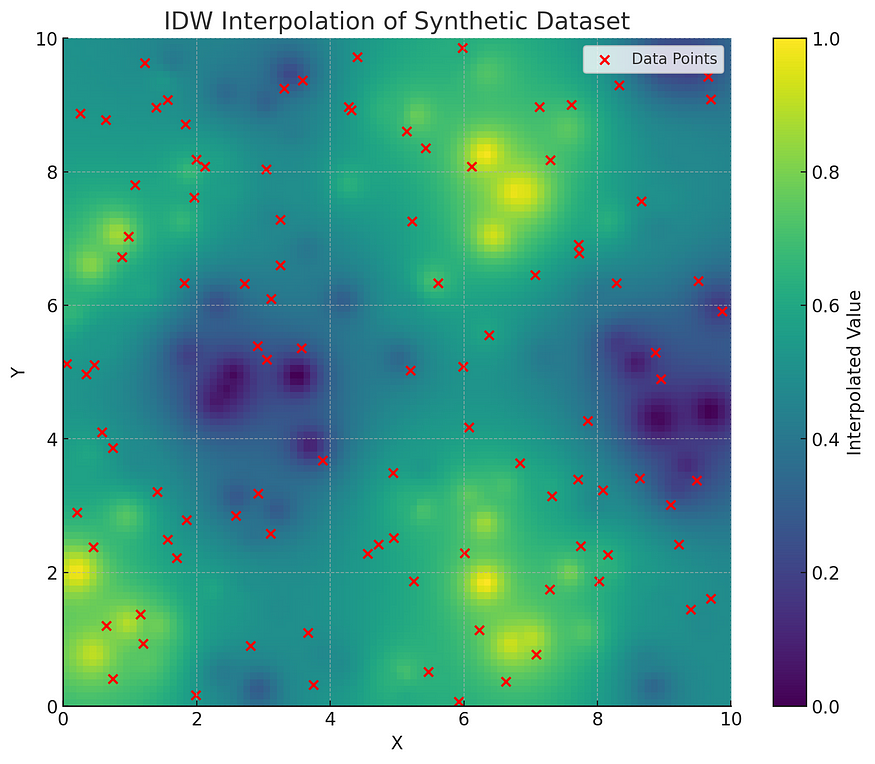
第一张图展示了我们生成的合成数据集,其中颜色表示每个点的值,结合了正弦和余弦函数以实现可变性。在此数据集中,点随机分布在 2D 空间中,模拟真实世界的空间数据不规则性。
第二张图显示了将反距离加权 (IDW) 插值应用于此数据集的结果。此处显示插值表面,颜色表示整个区域的插值值。红点表示原始数据点。IDW 方法有效地在网格上创建平滑梯度,根据附近点的加权平均值估计位置值。每个数据点对插值的影响随着距离的增加而减小,这遵循了IDW的核心原理。此示例演示了 IDW 在空间分析中的实用性,即从分散的数据点提供连续表面。
七、结论
反距离加权是空间分析的基石技术,因其在跨不同领域插值缺失数据的简单性和有效性而备受推崇。虽然它提供了一种基于邻近度估计值的简单方法,但其局限性需要谨慎应用,并且通常需要与其他插值方法进行补充,以进行更复杂的空间分析。随着 GIS 和空间数据在理解和管理我们的环境方面变得越来越不可或缺,像 IDW 这样的技术在弥合分散数据点和连续空间理解之间的差距方面发挥着关键作用。