分巧克力

题目描述

儿童节那天有 K位小朋友到小明家做客。
小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N块巧克力，其中第 i 块是 H_i×W_i 的方格组成的长方形。
为了公平起见，小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。
切出的巧克力需要满足：

1. 形状是正方形，边长是整数
2. 大小相同
   例如一块 6×5 的巧克力可以切出 6块 2×2 的巧克力或者 2 块 3×3的巧克力。
   当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

输入格式
第一行包含两个整数 N 和 K。
以下 N行每行包含两个整数 H_i和 W_i。
输入保证每位小朋友至少能获得一块 1×1 的巧克力。

输出格式
输出切出的正方形巧克力最大可能的边长。

数据范围
1≤N,K≤10⁵,
1≤H_i,W_i≤10⁵
输入样例：

2 10
6 5
5 6

输出样例：

2

二分算法

如果看不懂题目要求，画图就可以理解了，如下图：

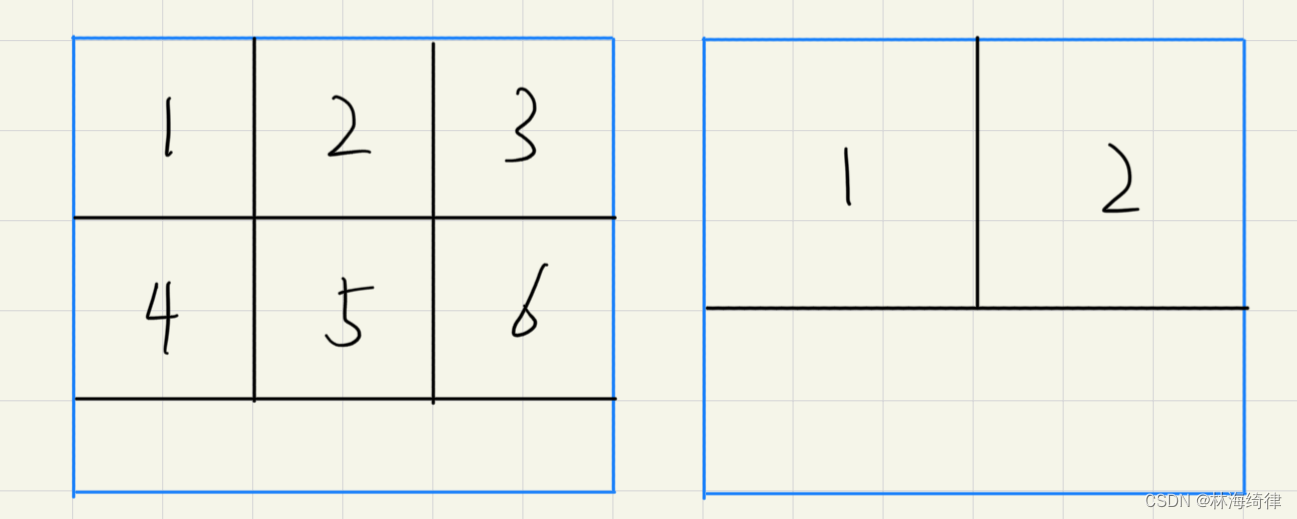
如果使用二分算法，那么切割的巧克力边长依题意最小为1，最大为最大巧克力的最小边，因此l=1,r=最大巧克力的最小边，因为要求出输出切出的正方形巧克力最大可能的边长，所以使用二分查找中的右查找得到最大值。

如何判断怎么从检查是否能从所有巧克力块中切出至少k块边长为z的正方形巧克力？
从上图可以看出，切割的块数=h/midw/mid。例如56的巧克力，能切割出的块数=5/26/2=23=6。

ps：在求r时我刚开始做的时候求的是所有巧克力的最小边，但这样子是不对的，因为当总巧克力足够多时，例如100块，里面的数据可能会有23的小巧克力，甚至11的小巧克力，这样的数据可以舍去，并不影响求输出切出的正方形巧克力，所以r的值应该为最大巧克力的最小边（所有巧克力的最小边长）

#include<bits/stdc++.h> // 包含C++标准库的所有头文件
using namespace std;

// 声明全局变量
int n, k, h[100010], w[100010]; // n为巧克力数量, k为小朋友数量, h和w分别存储每块巧克力的高和宽

// 检查是否能从所有巧克力块中切出至少k块边长为z的正方形巧克力
bool check(int z) {
    int count = 0; // 用于计算能切出的正方形巧克力的个数
    for (int i = 0; i < n; i++) {
        count += (h[i] / z) * (w[i] / z); // 计算第i块巧克力能切出多少个边长为z的正方形
        if (count >= k) return true; // 如果已经能切出至少k块，则返回true
    }
    return false; // 如果不能切出至少k块，则返回false
}

int main() {
    cin >> n >> k; // 输入巧克力的数量和小朋友的数量
    int i;
    int max_size = 0; // 存储所有巧克力中最长的边
    for (i = 0; i < n; i++) {
        cin >> h[i] >> w[i]; // 输入每块巧克力的高和宽
        max_size = max(max_size, min(h[i], w[i])); //最大巧克力的最小边
    }
    //二分查找——右查找：找最大值
    int l = 1, r = max_size; // 设置二分搜索的范围
    while (l < r) { // 当左边界小于右边界时，执行循环
        int mid = (l + r + 1) >> 1; // 计算中间值，向上取整
        if (check(mid)) l = mid; // 如果能切出足够多的巧克力，则向右收缩范围
        else r = mid - 1; // 如果不能切出足够多的巧克力，则向左收缩范围
    }
    cout << r; // 输出最大可能的边长
    return 0; // 程序结束
}

这段代码中，check 函数通过试验不同的 z 值来检查是否可以满足题目条件。二分搜索用于优化查找过程，它逐渐缩小查找边长 z 的范围，直到找到最大可能的边长。l 是查找范围的下界，r 是上界，mid 是每次迭代中的中间值。最终，二分搜索结束时的 r 值即为结果。