时序差分（TD）是强化学习的核心，其是蒙特卡罗（MC）和动态规划（DP）的结合。

1、TD 预测

TD 和 MC 都是利用经验来解决预测问题。一种非平稳环境的一般访问蒙特卡罗方法是
$$V(S_t)\leftarrow V(S_t)+\alpha \left[G_t-V(S_t)\right]$$

MC 方法必须等到事件结束才能确定 $V(S_t)$ 的增量（因为结束 $G_t$ 才是已知的），而 TD 方法只需要等到下一个时间步长。在时间 $t+1$ 时，立即生成一个目标，并使用观察到的奖励 $R_{t+1}$ 和估计值 $V(S_{t+1})$ 进行有用的更新，最简单的 TD 方法更新方式如下：
$$V(S_t)\leftarrow V(S_t)+\alpha \left[R_{t+1}+\gamma V(S_{t+1})-V(S_t)\right]$$

MC 方法更新的目标是 $G_t$，而 TD 方法的目标是 $R_{t+1}+\gamma V(S_{t+1})$。这种 TD 方法称为 $\mathrm{TD}(0)$。
$$\begin{array}{rl}{v}_{\pi }(s)& \doteq {\mathbb{E}}_{\pi }\left[G_t|S_t=s\right]\\ & ={\mathbb{E}}_{\pi }\left[R_{t+1}+\gamma G_{t+1}|S_t=s\right]\\ & ={\mathbb{E}}_{\pi }\left[R_{t+1}+\gamma v_{\pi }(S_{t+1})\right]\end{array}$$

由上式，MC 方法使用第二行的估计值作为目标，而 DP 方法使用第三行的估计值作为目标。MC 目标是一个估计值，因为期望值是未知的，我们是用平均样本收益代替实际的期望收益；DP 目标也是一个估计值，虽然环境模型完全已知，但是 $v_{\pi }(S_{t+1})$ 是未知的，使用的当前的估计值；TD 目标也是一个估计值，因为它对第三行中的期望值进行采样，且使用的当前的估计值而不是真实的 $v_{\pi }$。因此，TD 方法结合了 MC 的采样和 DP 的自举。

另外，$\mathrm{TD}(0)$ 算法中括号内是一种误差，即状态 $S_t$ 的当前估计值与更好的估计值 $R_{t+1}+\gamma V(S_{t+1})$ 的差异，这个量称为 $\mathrm{TD}$ 误差（$TDerror$），在强化学习中以各种形式出现：
$${\delta }_t\doteq R_{t+1}+\gamma V(S_{t+1})-V(S_t)$$

2、TD 预测的优点

显然，TD 方法比 DP 方法有一个优势，因为它无需环境模型已知。TD 方法比 MC 方法的一个明显的优势是，它以在线、完全增量的方式实现；另外 MC 方法需要等到一个回合结束，而 TD 方法只需要等待一个时间步，这很关键，某些特殊情形可能回合结束时间太长，甚至回合不会结束。

3、TD(0) 的最优性

假设只有有限的经验，例如 10 个回合或 100 个时间步长，在这种情况下，增量学习方法的常见手段是反复呈现经验，直到收敛到一个值。给定一个近似价值函数 $V$，MC 增量和 TD 增量

4、Sarsa：同策略 TD 控制

现在我们使用 TD 预测方法来解决控制问题，与之前一样，我们遵循广义策略迭代（GPI）的模式，与 MC 方法一样，我们面临着进行探索的需要，同样，方法分为两大类：同策略和异策略。本节提出一种同策略上的 TD 控制方法。

第一步是学习动作价值函数而不是状态价值函数，对于同策略方法，我们必须估计 $q_{\pi }(s,a),\forall s\in \mathcal{S},\forall a\in \mathcal{A}$，一个回合由状态和状态-动作对的交替序列组成：

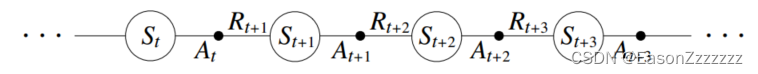
在前一章中，我们考虑从状态到状态的转换，并学习了状态的价值。现在我们考虑从状态-动作对到状态-动作对的转换，并学习状态-动作对的价值。形式上，这两种情况是一样的：它们都是带有奖励过程的马尔可夫链，保证 $\mathrm{TD}(0)$ 下状态价值收敛的定理也适用于动作价值的相应算法：
$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha \left[R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)\right]$$

5、Q-learning：异策略 TD 控制

强化学习的早期突破之一就是开发了一种被称为 Q-learning 的异策略 TD 控制算法，定义如下
$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha \left[R_{t+1}+\gamma \underset{a}{\max }Q(S_{t+1},a)-Q(S_t,A_t)\right]$$