目录

一. 线性规划

1.基本概念

线性规划的标准形式为：

线性规划的解：

线性规划三要素：

 灵敏度分析：

2.matlab的实现 

二. 整形规划

1.整型规划分类

2.基础模型 

 2.1  非线性约束条件的线性化

 3.模型求解

一.钢管下料问题

二.蒙特卡洛问题

---

一. 线性规划

1.基本概念

线性规划的标准形式为：

线性规划的解：

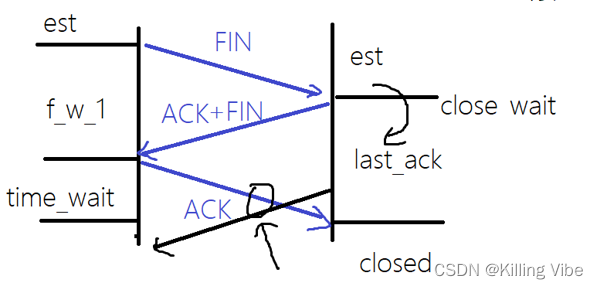
        可行解  满足约束条件(1.4)的解x向量，被称为线性规划问题的可行解，而使目标函数(1.3)达到最大值的可行解叫做最优解。

        可行域 所有可行解共同构成可行域，记作R

线性规划三要素：

 灵敏度分析：

2.matlab的实现 

线性回归基础概念

optimproblem函数详解

solve函数详解

基于问题的优化工作流

利用 optimproblem函数求解

二. 整形规划

1.整型规划分类

2.基础模型 

 2.1  非线性约束条件的线性化

1.相互排斥的约束条件

 

2.固定费用问题

 3.模型求解

Matlab中 intlinprog函数用法

 非线性求解

一.钢管下料问题

切割模式 

 

目标函数：

 

约束条件： 

目标一： 共27根，余27m

目标二：共25根，余35m

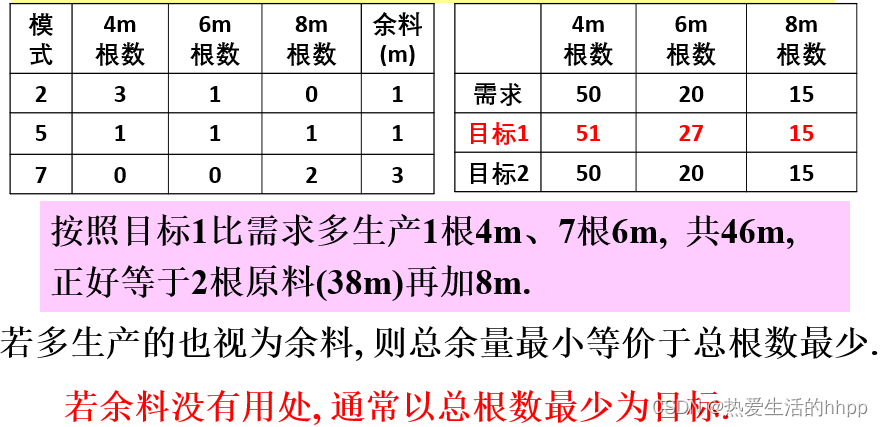
问题2

决策变量：

~按第i 种模式切割的原料钢管根数(i=1,2,3).

~ 第i 种切割模式下，每根原料钢管生产4m、5m、6m和8m长的钢管的数量.

 目标函数（总根数）:

约束条件： 

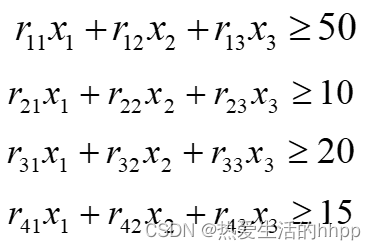
整数约束： xi ,r1i, r2i, r3i, r4i (i=1,2,3)为整数

每根余料要小于3

 

 

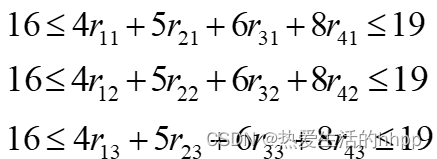
 寻找约束非线性多变量函数的最小值 - MATLAB fmincon - MathWorks 中国

二.蒙特卡洛问题

蒙特卡洛方法也称为计算机随机模拟方法，它源于世界著名的赌城—摩纳哥的Monte Carlo（蒙特卡洛）。它是基于对大量事件的统计结果来实现一些确定性问题的计算。使用蒙特卡洛方法必须使用计算机生成相关分布的随机数，MATLAB给出了生成各种随机数的命令。

 

例题：

 

function [f,g]=mengte(x);  %定义目标函数和约束条件
f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)-8*x(1)-2*x(2)-3*x(3)-...
x(4)-2*x(5);
g=[sum(x)-400
x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800
2*x(1)+x(2)+6*x(3)-200
x(3)+x(4)+5*x(5)-200];
end

clc, clear
%rng('shuffle')  %根据当前时间为随机数生成器提供种子
rng(0) %进行一致性比较，每次产生的随机数是一样的
p0=0; n=10^6; tic    %计时开始

for i=1:n
   x=randi([0,99],1,5); %产生一行五列的区间[0,99]上的随机整数
   [f,g]=mengte(x);
   if all(g<=0)
       if p0<f
           x0=x; p0=f; %记录下当前较好的解
       end
   end
end
x0, p0, toc    %计时结束