介绍
在计算机科学领域,有许多有趣的算法问题需要解决。其中之一就是判断在给定条件下是否存在逃脱路径的问题。本篇博客将介绍如何使用广度优先搜索(BFS)算法来解决这个问题。
问题背景
假设有一个二维平面上的迷宫,某人被困在迷宫中,需要从起点逃离到终点。但是,迷宫中有一些障碍物,人物无法通过障碍物移动。现在的问题是,是否存在一条路径可以使人物从起点逃离到终点,而不经过障碍物。
例题
在一个 106 x 106 的网格中,每个网格上方格的坐标为 (x, y) 。
现在从源方格 source = [sx, sy] 开始出发,意图赶往目标方格 target = [tx, ty] 。数组 blocked 是封锁的方格列表,其中每个 blocked[i] = [xi, yi] 表示坐标为 (xi, yi) 的方格是禁止通行的。
每次移动,都可以走到网格中在四个方向上相邻的方格,只要该方格 不 在给出的封锁列表 blocked 上。同时,不允许走出网格。
只有在可以通过一系列的移动从源方格 source 到达目标方格 target 时才返回 true。否则,返回 false
例题链接:. - 力扣(LeetCode)
解题思路:BFS + 给定障碍物所能围成的最大面积
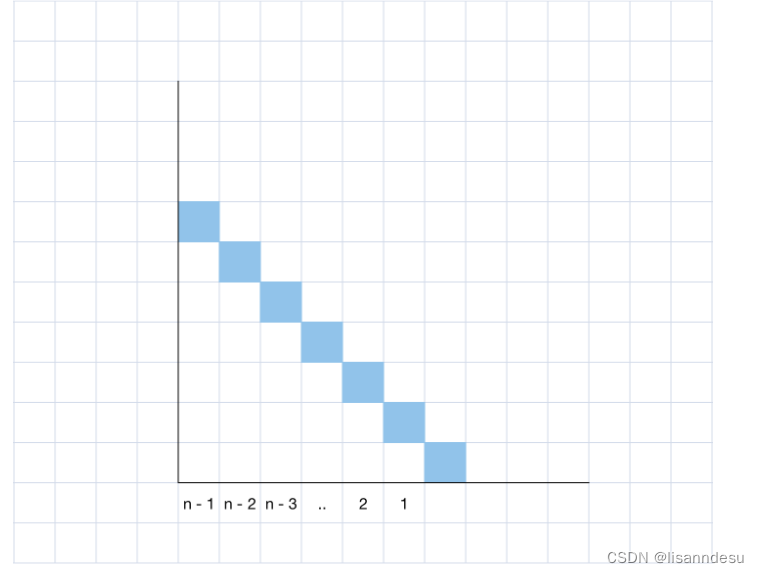
从 source 跑一遍 BFS,然后从 target跑一遍 BFS,同时设定一个最大访问点数量 MAX,若从两者出发能够访问的点数量都能超过 MAX,说明两点均没有被围住,最终必然会联通。其中MAX为len(blocked)个方块所能围成的最大面积,其为n(n-1)/2其中n=len(bloked),即当其排成斜线与边界围成直角三角形时,如图
- 初始化条件:将起点和终点作为初始条件,并将起点加入队列中。
- BFS搜索:
- 不断从队列中取出当前位置,然后向四个方向扩展搜索。
- 对于每一个邻居节点,检查是否越界、是否是障碍物或已经访问过的节点。
- 如果符合条件,则将该节点加入队列并标记为已访问。
- 继续下一轮搜索直到找到终点或者队列为空。
- 路径限制:
- 为了避免无限搜索,设置一个最大搜索次数 MAX,当已访问节点数超过 MAX 时,认为路径可能存在但无法判断。
- 返回结果:根据最终搜索结果,判断是否存在可行的逃脱路径
详细题解见文末链接
python代码实现
MAX = int(1e5) #blocked所能围成的最大面积为n(n-1)/2 (2n=len(blocked)),最大时小于1e5
BASE = int(131)
dircs = [[0,1], [0,-1], [1,0], [-1, 0]]
class Solution:
def isEscapePossible(self, blocked: List[List[int]], source: List[int], target: List[int]) -> bool:
queue = []
my_blocked = set()
blocked = {x*BASE+y for x, y in blocked}#二维转一维,高效查改
def bfs(a, b):
queue = [a]
my_blocked = set()
while len(queue) and len(my_blocked)<=MAX:
x, y = queue.pop()
if [x, y]==b:
return True
for dirc in dircs:
nx, ny = x+dirc[0], y+dirc[1]
if nx < 0 or nx>=1e6 or ny < 0 or ny>=1e6:# 防止超过地图边界
continue
if nx*BASE+ny in blocked or nx*BASE+ny in my_blocked:#防止重复计数
continue
my_blocked.add(nx*BASE+ny) #防止重复计数
queue.append([nx, ny])
return len(my_blocked)>MAX
return bfs(target, source) and bfs(source, target)
测试与结果
我们可以通过几组测试用例来验证代码的正确性,例如:
- 给定迷宫地图和起始点终止点坐标,判断是否存在可行的逃脱路径。
- 考虑不同大小的迷宫和障碍物分布情况,观察算法的执行效率和准确性。
时间复杂度O(N^2)
空间复杂度O(N^2)
(N为len(blocked))
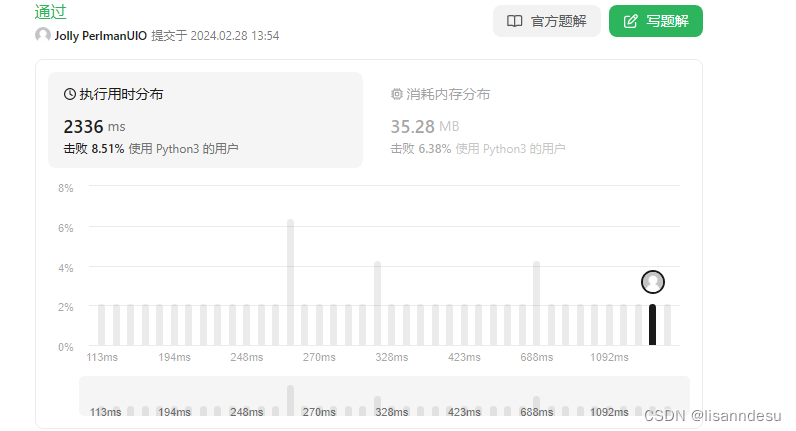
leetcode运行截图:
总结与展望
通过本篇博客,我们了解了如何使用 BFS 算法来解决逃脱路径判断问题。这种算法思想可以应用在许多实际场景中,如游戏中人物逃脱、路径规划等方面。未来,我们可以进一步优化算法,提高搜索效率,或者拓展到更复杂的迷宫问题中。
希望这篇博客能够帮助大家理解逃脱路径判断算法的实现方法。谢谢阅读!