基于FPGA的9/7整数小波变换和逆变换verilog实现,包含testbench

news2025/1/23 12:56:12

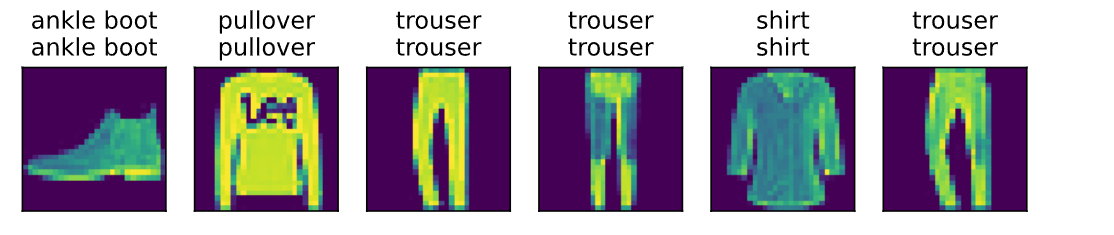
1.算法运行效果图预览

2.算法运行软件版本

3.部分核心程序

4.算法理论概述

4.1 9/7整数小波变换原理

4.2 逆变换过程

5.算法完整程序工程

1.算法运行效果图预览

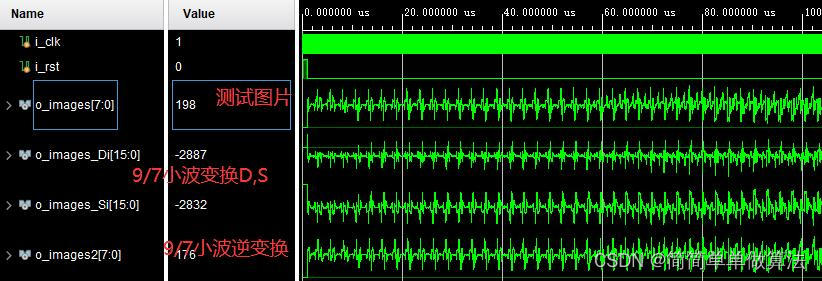
将测试结果导入到matlab显示

2.算法运行软件版本

vivado2019.2，matlab2022a

3.部分核心程序

`timescale 1ns / 1ps
//
// Company: 
// Engineer: 
// 
// Create Date: 2024/02/19 20:11:37
// Design Name: 
// Module Name: TEST_tops
// Project Name: 
// Target Devices: 
// Tool Versions: 
// Description: 
// 
// Dependencies: 
// 
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
// 
//


module TEST_tops();



reg       i_clk;
reg       i_rst;
wire[7:0]o_images;	
//9/7 wavelet
wire signed[15:0]o_images_Di;
wire signed[15:0]o_images_Si;
//9/7 dewavelet
wire       [7:0] o_images2;


tops tops_uut(
            .i_clk        (i_clk),
			   .i_rst        (i_rst),
 
				.o_images       (o_images),
				.o_images_Di       (o_images_Di),
                .o_images_Si       (o_images_Si),  
				.o_images2      (o_images2)
           );

initial
begin
     i_clk = 1'b0;
	  i_rst = 1'b1;
	  #1000
	  i_rst = 1'b0;

end	

integer fout1;
integer fout2;
integer fout3;
integer fout4;
initial begin
 fout1 = $fopen("A.txt","w");
 fout2 = $fopen("B.txt","w");
 fout3 = $fopen("C.txt","w"); 
 fout4 = $fopen("D.txt","w"); 
end

always @ (posedge i_clk)
 begin
	$fwrite(fout1,"%d\n",o_images);
	 $fwrite(fout2,"%d\n",o_images_Di);
	 $fwrite(fout3,"%d\n",o_images_Si);	 
	 $fwrite(fout4,"%d\n",o_images2);	
end
	
	
	
always #5 i_clk = ~i_clk;




endmodule
17_008m

4.算法理论概述

小波变换是一种在信号处理中广泛应用的数学工具，它能够提供信号在不同尺度和位置上的信息。在图像处理、数据压缩、噪声消除等领域，小波变换都发挥着重要作用。9/7整数小波变换是一种特别适用于无损或有损图像压缩的小波变换，它具有良好的能量集中性和对称性。现场可编程门阵列（FPGA）作为一种可重构的硬件平台，非常适合实现这种计算密集型的小波变换算法。

9/7整数小波变换基于两个主要的滤波器：一个低通滤波器（也称为尺度滤波器）和一个高通滤波器（也称为小波滤波器）。这两个滤波器分别用于提取信号的近似（低频）和细节（高频）信息。

4.1 9/7整数小波变换原理

9/7整数小波变换是一种离散小波变换（Discrete Wavelet Transform, DWT）算法，其中最常用的是Daubechies小波家族中的db2小波。该变换主要用于信号的多分辨率分析，通过低通滤波器（LPF）和高通滤波器（HPF）对输入数据进行滤波操作，分别得到近似系数（approximation coefficients）和细节系数（detail coefficients）。在9/7整数小波变换中，滤波器系数是整数，这使得计算过程可以实现无损精度。

对于一维信号x[n]，其连续小波变换可以表示为卷积形式：