"The only limit to our realization of tomorrow will be our doubts of today." - Franklin D. Roosevelt

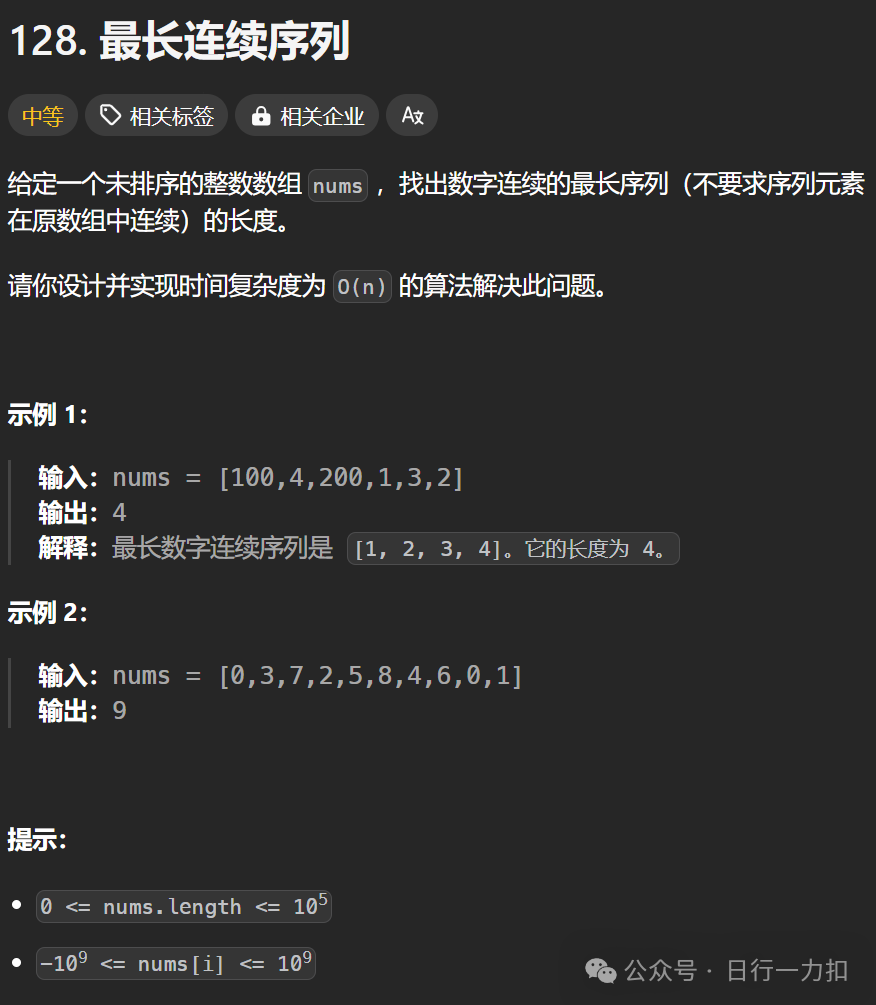
1. 题目描述
2. 题目分析与解析
2.1 思路一
题目要求我们使用时间复杂度为O(n)的解决方案,那么肯定就不能排序了。因为排序算法不可能达到O(n)的时间复杂度。
常见的排序算法包括:
冒泡排序(Bubble Sort):时间复杂度为O(n^2)。
选择排序(Selection Sort):时间复杂度为O(n^2)。
插入排序(Insertion Sort):时间复杂度为O(n^2)。
归并排序(Merge Sort):时间复杂度为O(n log n)。
快速排序(Quick Sort):平均时间复杂度为O(n log n),最坏情况下为O(n^2)。
堆排序(Heap Sort):时间复杂度为O(n log n)。
希尔排序(Shell Sort):时间复杂度取决于间隔序列的选择,一般为O(n log n)到O(n^2)。
计数排序(Counting Sort):时间复杂度为O(n + k),其中k是输入范围。
桶排序(Bucket Sort):时间复杂度为O(n + k),其中k是桶的数量。
基数排序(Radix Sort):时间复杂度为O(d * (n + k)),其中d是数字的位数,k是基数。
那就只有考虑怎么用空间换时间,也就是把每一个走过的信息存储起来,方便后续使用,才有可能达到O(n)的时间复杂度。
现在我们再来审一下题目,既然题目要求连续,这是一个核心特征,我们就要根据这个特征作为抓手,看它有什么性质,从而给出可能的解决方案。
什么是连续?
题目中提到的连续指的是如 {1,2,3,4,5,6,7}这样的数字,它有什么特点?是不是显而易见,每个数字之差相差1。根据这个性质能否想出解决方案?
是可以的。假设我们遍历数组的每一个元素,我要看当前数字是否能和其它之前遍历过的数字是否连续,那么就只需要判断是否在之前遍历的集合中是否有某个数字与它的绝对值之差等于1,也就是:
-
要么之前走过的某个数等于当前数+1
-
要么之前走过的某个数等于当前数-1
那么就可以知道这两个数字是连续的,就可以把现有连续的数字长度加一,那么就说明我们对于走过的数字不仅仅需要存储数字本身,还需要存储当前序列的长度。而又因为每加入一个数字,都是在当前数字串的基础上加在前面或者加在后面,所以我们在存储序列长度时只需要将序列的头部与尾部更新长度即可:
对于上图所示,如果对于一个新加入的数字5,那么我们发现存在6=5+1,所以我们就把5拼接在6前面,此时需要更新该 5,6,7串的首尾两个数字的 序列长度,将其更新为3。但是注意,对于如下的情况:
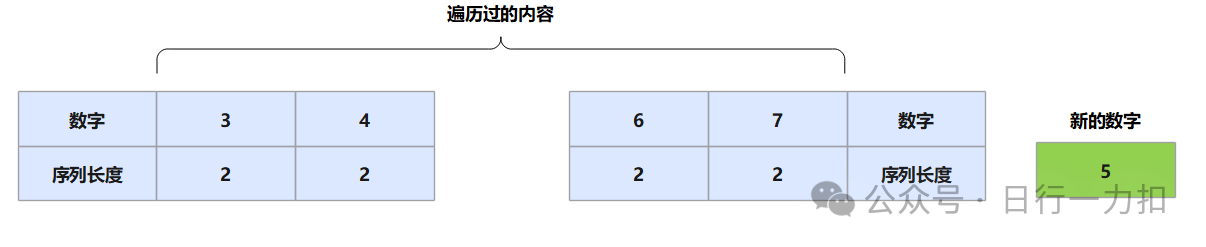
如上图所示,如果遍历到数字5,发现 5=4+1,而且 5+1=6,此时注意如果把该数字加入序列,那么就需要更新整体序列的第一个元素 3和最后一个元素 7的序列长度,将其变为5,如下:
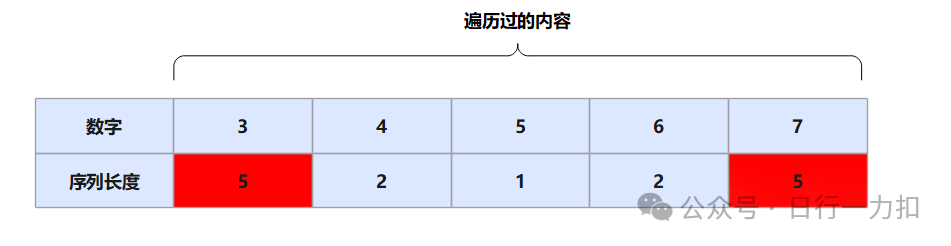
数字5处的对应的数字为1无需关系,只是一个默认数字。
所以根据以上的思路,我们就可以写出如下:
代码思路:
-
初始化:定义一个hashMap,用来存储走过的数字
-
遍历整个nums数组,判定当前数与某个走过的数字绝对值之差是否等于1,
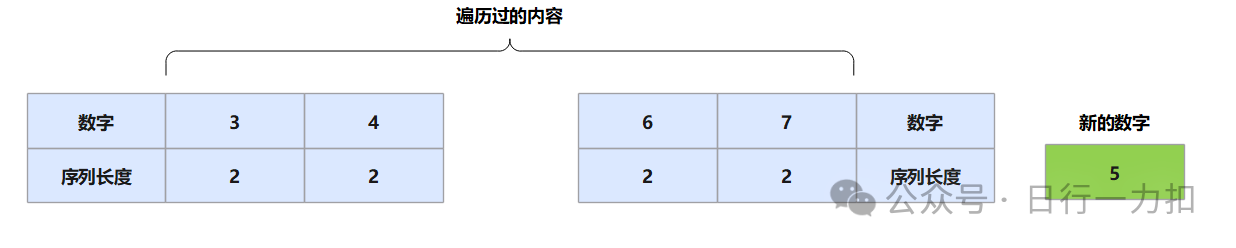
就需要更新
3和7处也就是序列合并后的头与尾的长度
那么就只需要更新当前数字和当前序列尾部数字对应的序列长度值
-
最后判断如果存在走过的数字中某个数小于当前数1,那么就对应下述情况:

此时只需要更新当前数字和当前序列头部数字对应的序列长度值
-
然后判断如果存在走过的数字中某个数大于当前数1,那么就对应下述情况:
-
先判断如果存在走过的数字中某个数大于当前数1,而且村子啊某个数小于当前数1,那么就对应下述情况:
-
-
遍历结束后hashMap中最大value即为结果
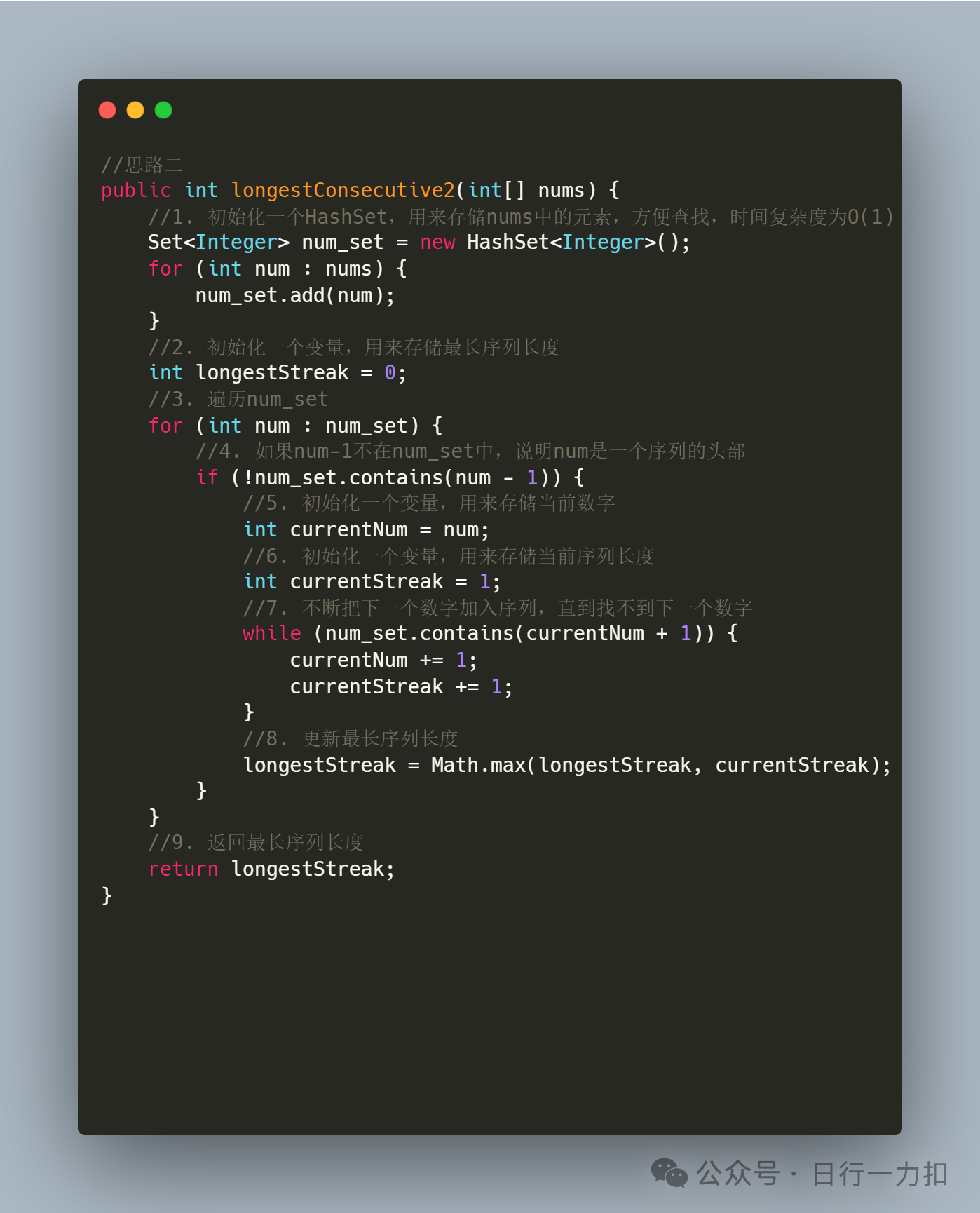
2.2 思路二
引自力扣官方

实现过程动图如下:
增加了判断跳过的逻辑之后,时间复杂度是多少呢?外层循环需要 O(n)的时间复杂度,只有当一个数是连续序列的第一个数的情况下才会进入内层循环,然后在内层循环中匹配连续序列中的数,因此数组中的每个数只会进入内层循环一次。根据上述分析可知,总时间复杂度为 O(n),符合题目要求。
在这里我主要给官方解析代码加一下注释,见后续代码实现。
3. 代码实现
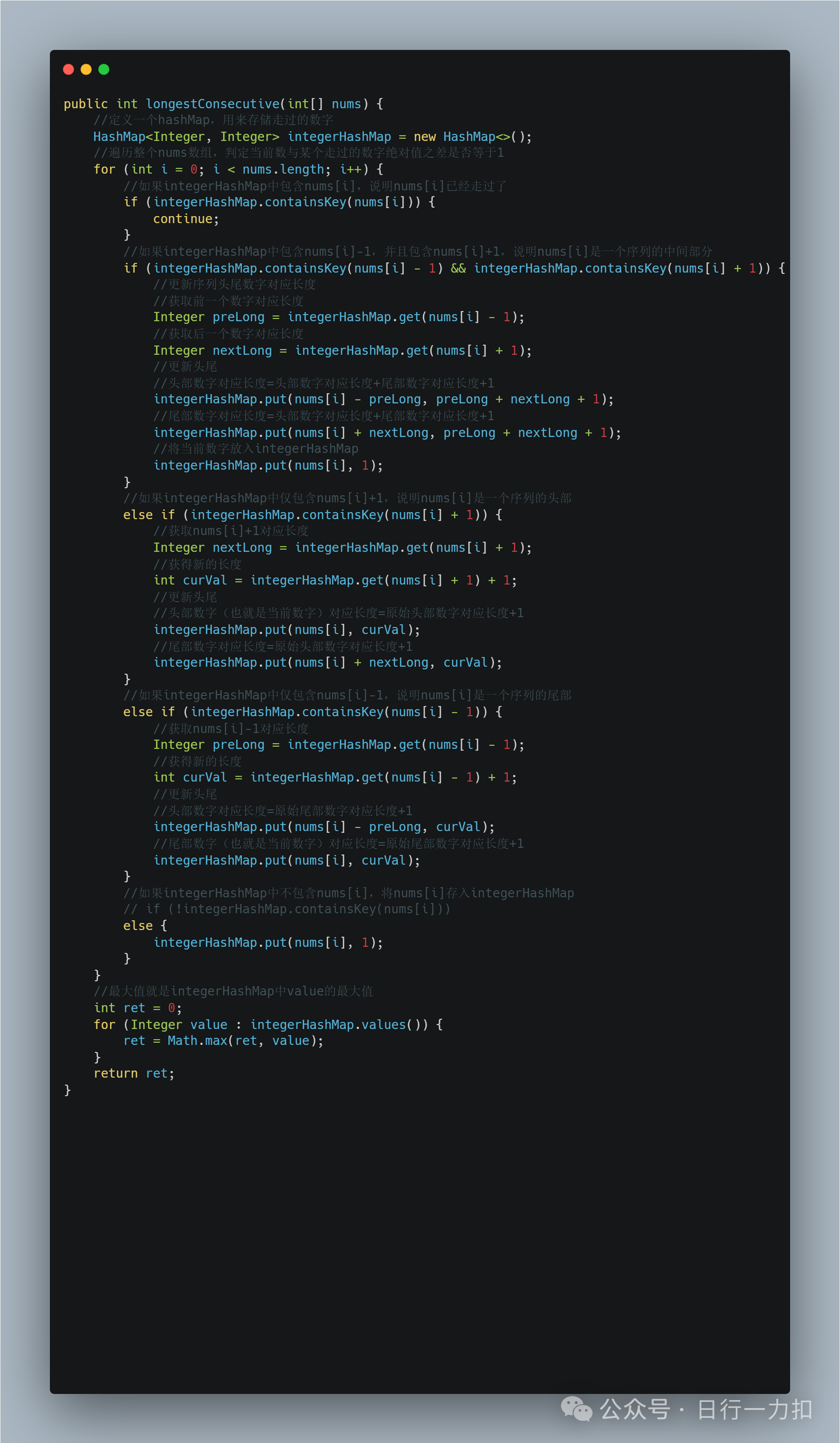
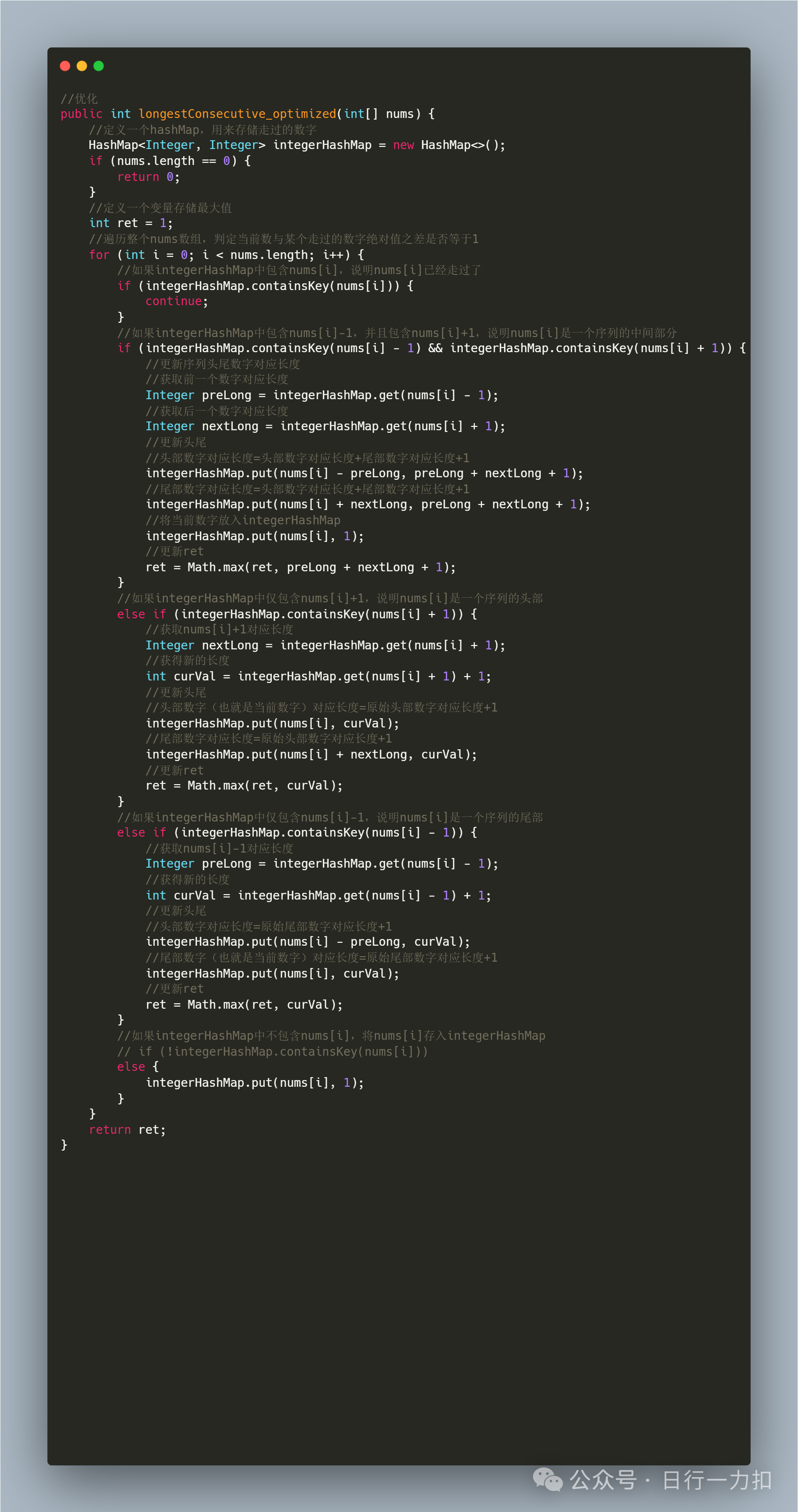
思路一优化
其实我们记住问题的本质,要寻找的是最大序列的长度,对应上述解题思路就是最大的value,那我们为何不用一个变量来存储最大的value,这样就没必要在遍历结束后从hashMap中找最大value了。因此我们可以进行优化如下:
3.2 思路二
4. 相关复杂度分析
方法一:优化版(longestConsecutive_optimized)
逻辑:
-
使用一个HashMap来追踪每个数字是否被访问过,以及它所在序列的长度。
-
遍历给定数组,对于每个元素,检查其前后元素是否存在于HashMap中,并据此更新序列的长度。
时间复杂度:
-
遍历给定数组一次,时间复杂度为
O(n)。 -
对于每个元素,查找和更新HashMap的操作均可在常数时间内完成(假设HashMap的操作为
O(1))。 -
因此,总的时间复杂度是
O(n)。
空间复杂度:
-
使用了一个HashMap来存储至多
n个元素及其对应的序列长度,因此空间复杂度为O(n)。
方法二:基于HashSet(longestConsecutive2)
逻辑:
-
首先,将所有元素存入HashSet中,以便快速查找任意元素是否存在。
-
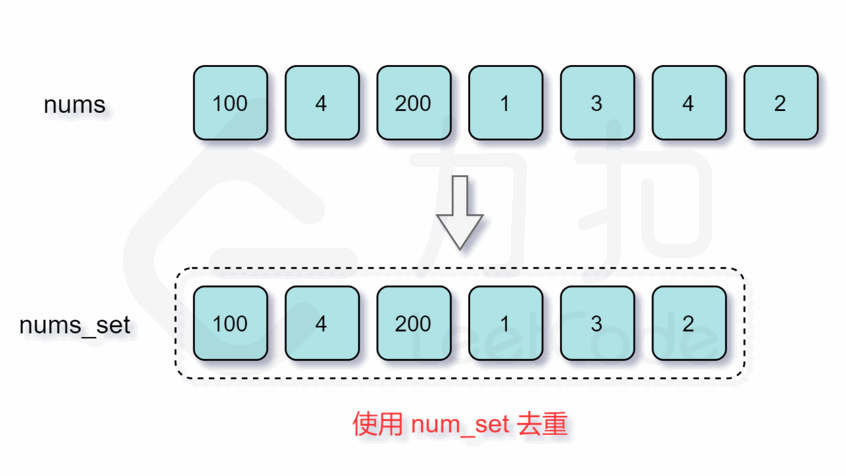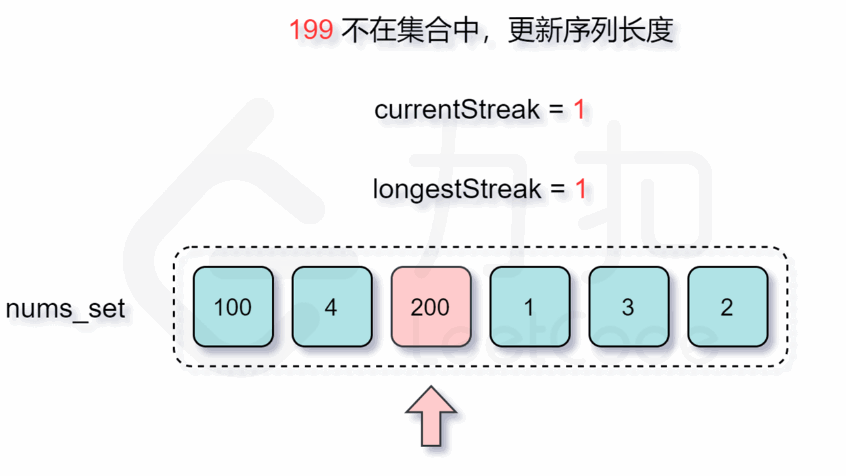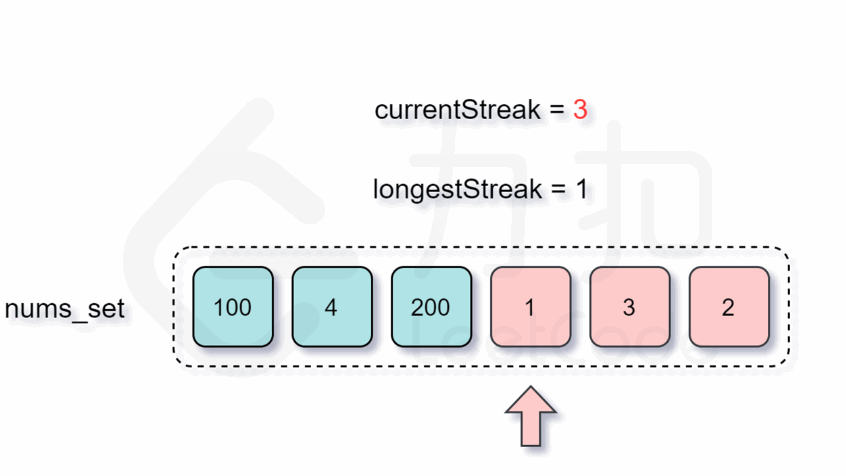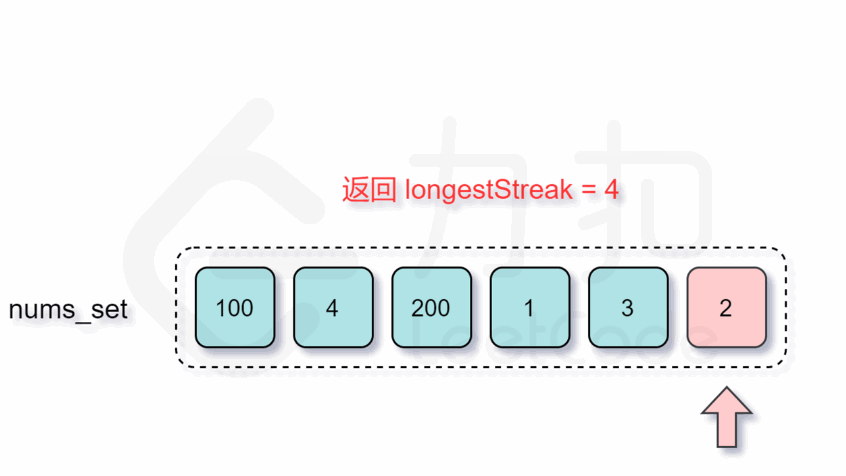
然后,遍历HashSet,对于每个元素,如果它的前一个元素不存在于HashSet中,则认为它是序列的起点,并从这个点开始尝试构建连续序列。
时间复杂度:
-
将所有元素添加到HashSet中的时间复杂度为
O(n)。 -
遍历HashSet的时间复杂度也为
O(n)。对于每个序列的起始元素,我们可能会在HashSet中进行多次查找(最坏情况下为序列长度次),但每个元素最多被访问两次(一次作为某个序列的一部分,另一次作为尝试找下一个元素)。因此,整体的时间复杂度依然是O(n)。
空间复杂度:
-
使用了一个HashSet来存储所有元素,空间复杂度为
O(n)。
总结
两种方法都具有O(n)的时间复杂度和O(n)的空间复杂度。主要区别在于实现细节和具体操作。优化版方法直接在遍历过程中更新和记录序列的长度,而基于HashSet的方法则是先构建一个集合,再通过这个集合找到所有可能的序列起点,从而构建序列。